5.5: La perpendicular es la más corta

Última actualización
Guardar como PDF

Page ID: 114847

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Lema$\PageIndex{1}$

Asumir$Q$ es el punto del pie de$P$ en la línea$\ell$. Entonces la desigualdad

$PX > PQ$

se mantiene para cualquier punto$X$ en$\ell$ distinto de$Q$.

Si$P, Q$, y$\ell$ son como arriba, entonces$PQ$ se llama la distancia de$P$ a$\ell$.

Prueba

Si$P \in \ell$, entonces el resultado sigue desde$PQ = 0$. Además suponemos que$P \not\in \ell$.

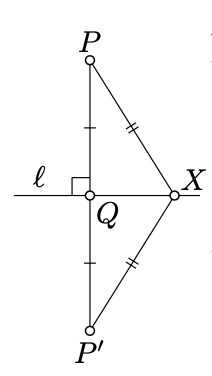
$2021-02-04 1.41.36.png$

Que$P'$ sea el reflejo del$P$ otro lado de la línea$\ell$. Tenga en cuenta que$Q$ es el punto medio de$[PP']$ y$\ell$ es la bisectriz perpendicular de$[PP']$. Por lo tanto

$PX = P'X$y$PQ = P'Q = \dfrac{1}{2} \cdot PP'$

Tenga en cuenta que$\ell$ se reúne$[PP']$ sólo en el punto$Q$. Por lo tanto,$X \not\in [PP']$; por desigualdad triangular y Corolario 4.4.1,

$PX + P'X > PP'$

y de ahí el resultado:$PX > PQ$.

Ejercicio$\PageIndex{1}$

Supongamos que$\angle ABC$ es correcto u obtuso. Demostrar que

$AC > AB.$

Pista

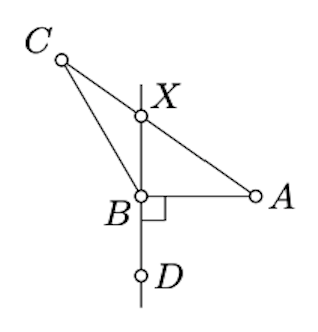
$2021-02-04 1.48.35.png$

Si$\angle ABC$ es correcto, la declaración se desprende de Lemma$\PageIndex{1}$. Por lo tanto, podemos suponer que$\angle ABC$ es obtuso.

Dibuja una línea$(BD)$ perpendicular a$(BA)$. Ya que$\angle ABC$ es obtuso, los ángulos$DBA$ y$DBC$ tienen signos opuestos.

Por Corolario 3.4.1,$A$ y$C$ se encuentra en lados opuestos de$(BD)$. En particular,$[AC]$ se cruza$(BD)$ en un punto; denotarlo por$X$.

Tenga en cuenta que$AX < AC$ y por Lemma$\PageIndex{1}$,$AB \le AX$.

Ejercicio$\PageIndex{2}$

Supongamos que$\triangle ABC$ tiene ángulo recto en$C$. Demuestre que para cualquier$X \in [AC]$ la distancia de$X$ a$(AB)$ es menor que$AB$.

Pista

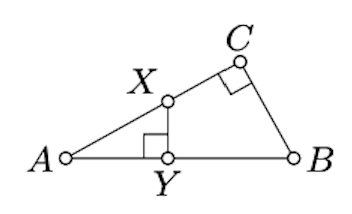
$2021-02-04 1.54.06.png$

Deja$Y$ ser el punto del pie de$X$ on$(AB)$. Aplica Lemma$\PageIndex{1}$ para demostrarlo$XY < AX \le AC < AB$.

Lema\(\PageIndex{1}\)

Ejercicio\(\PageIndex{1}\)

Ejercicio\(\PageIndex{2}\)