6.2: Teorema de Pitágoras

Última actualización
Guardar como PDF

Page ID: 114360

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Un triángulo se llama a la derecha si uno de sus ángulos es recto. El lado opuesto al ángulo recto se llama hipotenusa. Los lados adyacentes al ángulo recto se llaman patas.

Teorema$\PageIndex{1}$

Supongamos que$\triangle ABC$ es un triángulo rectángulo con el ángulo recto en$C$. Entonces

$AC^2 + BC^2 = AB^2.$

Prueba

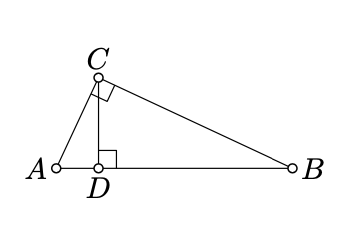
$2021-02-08 10.52.32.png$

Deja$D$ ser el punto del pie de$C$ on$(AB)$.

Según Lemma 5.5.1,

$AD < AC < AB$

$BD < BC < AB.$

Por lo tanto,$D$ se encuentra entre$A$ y$B$; en particular,

\[AD + BD = AB.\]

Tenga en cuenta que por la condición de similitud AA, tenemos

$\triangle ADC \sim \triangle ACB \sim \triangle CDB.$

En particular,

\[\dfrac{AD}{AC} = \dfrac{AC}{AB} \text{ and } \dfrac{BD}{BC} = \dfrac{BC}{BA}.\]

Reescribamos las dos identidades en 6.2.2:

$AC^2 = AB \cdot AD$y$BC^2 = AB \cdot BD$.

Resumiendo estas dos identidades y aplicando 6.2.1, obtenemos que

$AC^2 + BC^2 = AB \cdot (AD + BD) = AB^2.$

Ejercicio$\PageIndex{1}$

Asumir$A, B, C$, y$D$ son como en la prueba anterior. Demostrar que

$CD^2 = AD \cdot BD.$

El siguiente ejercicio es lo contrario al teorema de Pitágoras.

Pista: Aplica eso$\triangle ADC \sim \triangle CDB$.

Ejercicio$\PageIndex{2}$

Supongamos que$ABC$ es un triángulo tal que

$AC^2 + BC^2 = AB^2.$

Demostrar que el ángulo a$C$ es correcto.

Pista: Aplicar el teorema de Pitágoras$\PageIndex{1}$ y la condición de congruencia SSS

Teorema\(\PageIndex{1}\)

Ejercicio\(\PageIndex{1}\)

Ejercicio\(\PageIndex{2}\)