7.4: Ángulos de triángulos

Última actualización
Guardar como PDF

Page ID: 114416

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Teorema$\PageIndex{1}$

En cualquiera$\triangle ABC$, tenemos

$\measuredangle ABC + \measuredangle BCA + \measuredangle CAB \equiv \pi.$

Prueba

Primero tenga en cuenta que si$\triangle ABC$ es degenerado, entonces la igualdad se desprende del Corolario 2.4.1. Además suponemos que no$\triangle ABC$ es degenerado.

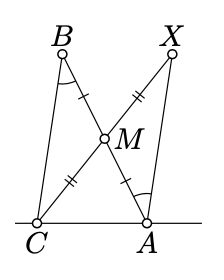
$2021-02-09 10.46.27.png$

Dejar$X$ ser el reflejo de$C$ a través del punto medio$M$ de$[AB]$. Por Proposición 7.2.1$\measuredangle BAX = \measuredangle ABC$. Tenga en cuenta que$(AX)$ es un reflejo de lo$(CB)$ ancho$M$; por lo tanto por el Teorema 7.2.1,$(AX) \parallel (CB)$.

Desde$[BM]$ y$[MX]$ no se cruzan$(CA)$, los puntos$B, M$, y$X$ se encuentran en el mismo lado de$(CA)$. Aplicando la propiedad transversal para$(CA)$ lo transversal a$(AX)$ y$(CB)$, obtenemos que

\[\measuredangle BCA + \measuredangle CAX \equiv \pi.\]

Desde entonces$\measuredangle BAX = \measuredangle ABC$, tenemos

$\measuredangle CAX \equiv \measuredangle CAB + \measuredangle ABC$

Esta última identidad y 7.4.1 implican el teorema.

Ejercicio$\PageIndex{1}$

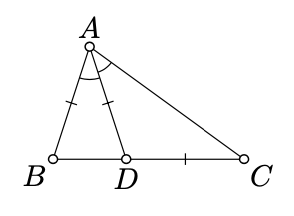
$2021-02-09 10.56.33.png$

Dejar$\triangle ABC$ ser un triángulo no degenerado. Supongamos que hay un punto$D \in [BC]$ tal que

$\measuredangle BAD \equiv \measuredangle DAC, BA = AD = DC.$

Encuentra los ángulos de$\triangle ABC$.

Sugerencia: Aplicar dos veces Teorema 4.3.1 y dos veces Teorema$\PageIndex{1}$.

Ejercicio$\PageIndex{2}$

Demostrar que

$|\measuredangle ABC| + |\measuredangle BCA| + |\measuredangle CAB| = \pi$

para cualquier$\triangle ABC$.

Sugerencia

Si$\triangle ABC$ es degenerado, entonces una de las medidas de ángulo es$\pi$ y las otras dos son 0. De ahí el resultado.

Supongamos que no$\triangle ABC$ es degenerado. Establecer$\alpha = \measuredangle CAB$,$\beta = \measuredangle ABC$, y$\gamma = \measuredangle BCA$.

Por el Teorema 3.3.1, podemos suponer que$0 < \alpha, \beta, \gamma < \pi$. Por lo tanto,

\[0 > \alpha + \beta + \gamma < 3 \cdot \pi.\]

Por teorema$\Pageindex{1}$,

\[\alpha + \beta +\gamma \equiv \pi.\]

De 7.4.2 y 7.4.3 sigue el resultado.

Ejercicio$\PageIndex{3}$

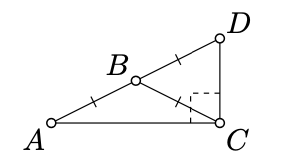
Dejar$\triangle ABC$ ser un triángulo no degenerado de isóselas con la base$[AC]$. Supongamos que$D$ es un reflejo de$A$ lo ancho$B$. Demuestre que$\angle ACD$ es correcto.

$2021-02-09 10.58.59.png$

Sugerencia: Aplicar dos veces Teorema 4.3.1 y dos veces Teorema$\PageIndex{1}$.

Ejercicio$\PageIndex{4}$

Dejar$\triangle ABC$ ser un triángel isósceles no degenerado con base$[AC]$. Supongamos que un círculo está pasando$A$, centrado en un punto sobre$[AB]$, y tangente a$(BC)$ en el punto$X$. $\measuredangle CAX = \pm \dfrac{\pi}{4}$Demuéstralo.

Sugerencia

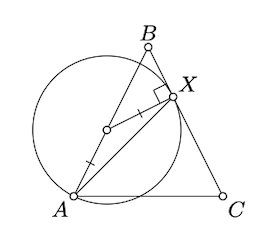
$2021-02-09 11.06.53.png$

Supongamos que$O$ denota el centro del círculo.

Tenga en cuenta que$\triangle AOX$ es isósceles y$\angle OXC$ tiene razón. Aplicando Teorema$\PageIndex{1}$ y Teorema 4.3.1 y simplificando, deberíamos obtener$4 \cdot \measuredangle CAX \equiv \pi$.

Demostrar que$\angle CAX$ tiene que ser agudo. De ello se deduce entonces eso$\measuredangle CAX = \pm \dfrac{\pi}{4}$.

Ejercicio$\PageIndex{5}$

Demostrar que para cualquier cuadrilátero$ABCD$, tenemos

$\measuredangle ABC + \measuredangle BCD + \measuredangle CDA + \measuredangle DAB \equiv 0$.

Sugerencia: Aplicar Teorema$\PageIndex{1}$ a$\triangle ABC$ y$\triangle BDA$.

Teorema\(\PageIndex{1}\)

Ejercicio\(\PageIndex{1}\)

Ejercicio\(\PageIndex{2}\)

Ejercicio\(\PageIndex{3}\)

Ejercicio\(\PageIndex{4}\)

Ejercicio\(\PageIndex{5}\)