7.3: Propiedad Transversal
- Page ID
- 114423
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Si la línea\(t\) se cruza con cada línea\(\ell\) y\(m\) en un punto, entonces decimos que\(t\) es una transversal a\(\ell\) y\(m\). Por ejemplo, en el diagrama, la línea (\(CB\)) es una transversal a (\(AB\)) y (\(CD\)).
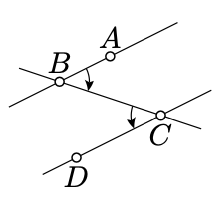
\((AB) \parallel (CD)\)si y solo si
\[2 \cdot (\measuredangle ABC + \measuredangle BCD) \equiv 0. \nonumber\]
Equivalentemente
\(\measuredangle ABC + \measuredangle BCD \equiv 0\)o\(\measuredangle ABC + \measuredangle BCD \equiv \pi.\)
Por otra parte\((AB) \ne (CD)\), si, entonces en el primer caso,\(A\) y se\(D\) encuentran en lados opuestos de\((BC)\); en el segundo caso,\(A\) y se\(D\) encuentran en los mismos lados de\((BC)\).
- Prueba
-
“solo si” parte. Denotar por\(O\) el punto medio de\([BC]\).
Asumir\((AB) \parallel (CD)\). Según el Teorema 7.2.1,\((CD)\) es un reflejo de\((AB)\) a través\(O\).
Que\(A'\) sea el reflejo de\(A\) través\(O\). Entonces\(A' \in (CD)\) y por la Proposición 7.2.1 tenemos que
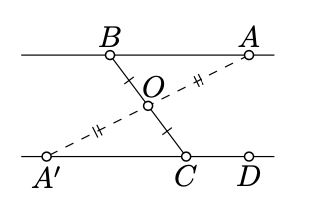
\[\measuredangle ABO = \measuredangle A'CO.\]
Tenga en cuenta que
\[\measuredangle ABO \equiv \measuredangle ABC, \ \ \ \ \measuredangle A'CO \equiv \measuredangle BCA'.\]
Dado que\(A', C\) y\(D\) se encuentran en una línea, el Ejercicio 2.4.2 implica que
\[2 \cdot \measuredangle BCD \equiv 2 \cdot \measuredangle BCA'.\]
Por último señalar que 7.3.2, 7.3.3 y 7.3.4 implican 7.3.1.
“Si” -parte. Por Teorema 7.2.1 hay una línea única\((CD)\) a través\(C\) que es paralela a\((AB)\). De la parte “solo si” sabemos que 7.3.1 sostiene.
Por otro lado, hay una línea única\((CD)\) tal que 7.3.1 sostiene. En efecto, supongamos que hay dos líneas de este tipo\((CD)\) y\((CD')\), entonces
\(2 \cdot (\measuredangle ABC + \measuredangle BCD) \equiv 2 \cdot (\measuredangle ABC + \measuredangle BCD') \equiv 0\).
Por lo tanto\(2 \cdot \measuredangle BCD \equiv 2 \cdot BCD'\) y por el Ejercicio 2.4.2\(D' \in (CD)\),, o equivalentemente la línea\((CD)\) coincide con\((CD')\).
Por lo tanto si 7.3.1 se mantiene, entonces\((CD) \parallel (AB)\).
Por último, si\((AB) \ne (CD)\) y\(A\) y\(D\) se encuentran en los lados opuestos de\((BC)\), entonces\(\angle ABC\) y\(\angle BCD\) tienen signos opuestos. Por lo tanto
\(-\pi < \measuredangle ABC + \measuredangle BCD < \pi.\)
Aplicando 7.3.1, obtenemos\(\measuredangle ABC + \measuredangle BCD = 0\).
Del mismo modo si\(A\) y se\(D\) encuentran en el mismo lado de\((BC)\), entonces\(\angle ABC\) y\(\angle BCD\) tienen el mismo signo. Por lo tanto
\(0 < |\measuredangle ABC + \measuredangle BCD| < 2\cdot \pi\)
y 7.3.1 implica eso\(\measurdangle ABC + \measuredangle BCD \equiv \pi\).
\(\triangle ABC\)Sea un triángulo no degenerado, y\(P\) se encuentra entre\(A\) y\(B\). Supongamos que una línea\(\ell\) pasa a través\(P\) y es paralela a\((AC)\). Demostrar que\(\ell\) cruza el costado\([BC]\) en otro punto, digamos\(Q\), y
\(\triangle ABC \sim \triangle PBQ.\)
En particular,
\(\dfrac{PB}{AB} = \dfrac{QB}{CB}.\)
- Pista
-
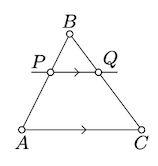
Ya que\(\ell \parallel (AC)\), no puede cruzar\([AC]\). Por el teorema de Pasch (Teorema 3.4.1),\(\ell\) tiene que cruzar otro lado de\(\triangle ABC\). Por lo tanto\(\ell\) cruzar\([BC]\); denotar el punto de intersección por\(Q\).
Utilizar la propiedad transversal (Teorema\(\PageIndex{1}\)) para mostrar eso\(\measuredangle BAC = \measuredangle BPQ\). El mismo argumento demuestra que\(\measuredangel ACB = \measuredangle PQB\); queda por aplicar la condición de similitud AA.
Trisecta un segmento dado con una regla y una brújula.
- Contestar
-
Supongamos que necesitamos trisectar segmento\([AB]\). Construye una línea\(\ell \ne (AB)\) con cuatro puntos\(A, C_1, C_2, C_3\) tales que\(C_1\) y\(C_2\) trisecta\([AC_3]\). Dibuja la línea\((BC_3)\) y dibuja líneas paralelas a través\(C_1\) y\(C_2\). Los puntos de intersecciones de estas dos líneas con\((AB)\) trisectan el segmento\([AB]\).