7.5: Paralelogramos
- Page ID
- 114399
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)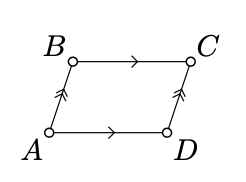
Un cuadrilátero\(ABCD\) en el plano euclidiano se llama nondegenerate si no hay tres puntos de\(A, B, C, D\) mentira en una línea.
Un cuadrilátero no degenerado se denomina paralelogramo si sus lados opuestos son paralelos.
Cualquier paralelogramo es centralmente simétrico con respecto a un punto medio de una de sus diagolales.
En particular, si\(\square ABCD\) es un paralelogramo, entonces
a) sus diagonales\([AC]\) y se\([BD]\) cruzan entre sí en sus puntos medios;
b)\(\measuredangle ABC = \measuredangle CDA\);
c)\(AB = CD\).
- Prueba
-
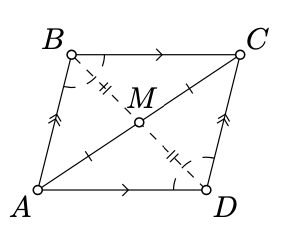
Dejar\(\square ABCD\) ser un paralelogramo. Denotar por\(M\) el punto medio de\([AC]\).
Ya que\((AB)\parallel (CD)\), el Teorema 7.2.1 implica que\((CD)\) es un reflejo de\((AB)\) través\(M\). De la misma manera\((BC)\) es un reflejo de\((DA)\) lo ancho\(M\). Dado que no\(\square ABCD\) es degenerado, se deduce que\(D\) es un reflejo de\(B\) través\(M\); en otras palabras,\(M\) es el punto medio de\([BD]\).
Las declaraciones restantes siguen ya que la reflexión a través\(M\) es un movimiento directo del plano (ver Proposición 7.2.1).
Asumir\(ABCD\) es un cuadrilátero tal que
\(AB = CD = BC = DA.\)
Tal que\(ABCD\) es un paralelogramo.
- Sugerencia
-
Ya que\(\triangle ABC\) es isósceles,\(\measuredangle CAB = \measuredangle BCA\).
Por SSS,\(\triangle ABC \cong \triangle CDA\). Por lo tanto,\(\pm \measuredangle DCA = \measuredangle BCA = \measuredangle CAB\).
Ya que\(D \ne C\), obtenemos “-” en la última fórmula. Utilice la propiedad transversal (Teorema 7.3.1) para demostrarlo\((AB) \parallel (CD)\). Repite el argumento para demostrarlo\((AD) \parallel (BC)\).
Un cuadrilátero como en el ejercicio anterior se llama rombo.
Un cuadrilátero ABCD se llama rectángulo si los ángulos ABC, BCD, CDA y DAB son correctos. Tenga en cuenta que de acuerdo con la propiedad transversal (Teorema 7.3.1), cualquier rectángulo es un paralelogramo.
Un rectángulo con lados iguales se llama cuadrado.
Mostrar que el paralelogramo\(ABCD\) es un rectángulo si y solo si\(AC = BD\).
- Sugerencia
-
Por Lemma\(\PageIndex{1}\) y SSS,\(AC = BD\) si y sólo si\(\angle ABC = \pm \measuredangle BCD\). Por la propiedad transversal (Teorema 7.3.1),\(\measuredangle ABC + \measuredangle BCD \equiv \pi\).
Por lo tanto,\(AC = BD\) si y sólo si\(\measuredangle ABC = \measuredangle BCD = \pm \dfrac{\pi}{2}\).
Mostrar que el paralelogramo\(ABCD\) es un rombo si y solo si\((AC) \perp (BD)\).
- Sugerencia
-
Arreglar un paralelogramo\(ABCD\). Por Lemma\(\PageIndex{1}\), sus diagonales\([AC]\) y\([BD]\) tienen un punto medio común; denotarlo por\(M\).
Usa SSS y Lemma\(\PageIndex{1}\) para demostrar que
\(AB = CD \Leftrightarrow \triangle AMB \cong \triangle AMD \Leftrightarrow \measuredangle AMB = \pm \dfrac{\pi}{2}.\)
Asumir\(\ell \parallel m\), y\(X, Y \in m\). Dejar\(X'\) y\(Y'\) denotar los puntos del pie de\(X\) y\(Y\) seguir\(\ell\). Tenga en cuenta que\(\square XYY'X'\) es un rectángulo. Por Lemma\(\PageIndex{1}\),\(XX' = YY'\). Es decir, cualquier punto en\(m\) se encuentra a la misma distancia de\(\ell\). Esta distancia se llama la distancia entre\(\ell\) y\(m\).