9.3: Puntos en un círculo común
- Page ID
- 114829
Recordemos que el diámetro de un círculo es un acorde que pasa por el centro. Si\([XY]\) es el diámetro de un círculo con centro\(O\), entonces\(\measuredangle XOY = \pi\). De ahí que el Teorema 9.2.1 implica lo siguiente:
Supongamos que\(\Gamma\) es un círculo con el diámetro\([AB]\). Un triángulo\(ABC\) tiene ángulo recto en\(C\) si y solo si\(C \in \Gamma\).
Dados cuatro puntos\(A, B, A'\), y\(B'\), construir un punto\(Z\) tal que ambos ángulos\(AZB\) y\(A'ZB'\) sean rectos.
- Pista
-
Construir los círculos\(\Gamma\) y\(\Gamma'\) en los diámetros\([AB]\) y\([A'B']\) respectivamente. Por Corolario\(\PageIndex{1}\), cualquier punto\(Z\) de la intersección\(\Gamma \cap \Gamma'\) servirá.
\(\triangle ABC\)Sea un triángulo no degenerado,\(A'\) y\(B'\) sean puntos de altitudes a pie desde\(A\) y\(B\) respetuosamente. Demostrar que los cuatro puntos\(A, B, A'\), y\(B'\) se encuentran en un círculo. ¿Cuál es el centro de este círculo?
- Pista
-
Tenga en cuenta que\(\measuredangle AA'B = \pm \dfrac{\pi}{2}\) y\(\measuredangle AB'B = \pm \dfrac{\pi}{2}\). Después aplicar Corolario\(\PageIndex{2}\) a\(\square AA'BB'\).
Si\(O\) es el centro del círculo, entonces\(\measuredangle AOB \equiv 2 \cdot \measuredangle AA'B \equiv \pi\). Es decir,\(O\) es el punto medio de\([AB]\).
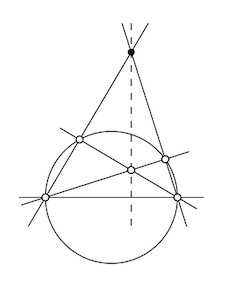
Supongamos que se da una línea\(\ell\), un círculo con su centro encendido\(\ell\) y un punto\(P \not\in \ell\). Hacer una construcción solo regla de la perpendicular a\(\ell\) de\(P\).
- Pista
-
Adivina la construcción a partir del diagrama. Para probarlo, aplicar el Teorema 8.2.1 y Corolario\(\PageIndex{1}\).
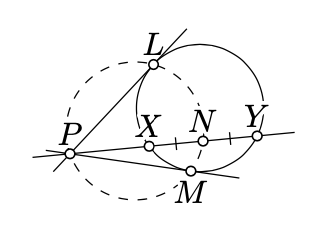
Supongamos que las líneas\(\ell\),\(m\) y\(n\) pasan a través de un punto\(P\); las líneas\(\ell\) y\(m\) son tangentes a un círculo\(\Gamma\) en\(L\) y\(M\); la línea\(n\) se cruza\(\Gamma\) en dos puntos\(X\) y\(Y\). Dejar\(N\) ser el punto medio de\([XY]\). Demostrar que los puntos\(P, L, M\), y\(N\) se encuentran en un círculo.
Decimos que un cuadriángulo\(ABCD\) se inscribe en círculo\(\Gamma\) si todos los puntos\(A, B, C\), y\(D\) se encuentran sobre\(\Gamma\).
- Pista
-
Denotar por\(O\) el centro de\(\Gamma\). Use Corolario\(\PageIndex{1}\) para mostrar que el punto se encuentra en el círculo con diámetro\([PO]\).
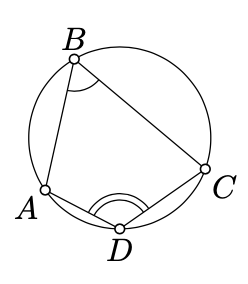
Un cuadriángulo no degenerado\(ABCD\) se inscribe en un círculo si y solo si
\(2 \cdot \measuredangle ABC \equiv 2 \cdot \measuredangle ADC.\)
- Prueba
-
Ya que no\(\square ABCD\) es degenerado, así es\(\triangle ABC\). Dejar\(O\) y\(\Gamma\) denotar el circulcenter y circumcircle de\(\triangle ABC\) (existen por el Ejercicio 8.1.1).
Según el Teorema 9.2.1,
\(2 \cdot \measuredangle ABC \equiv \measuredangle AOC\).
Del mismo teorema,\(D \ni \Gamma\) si y solo si
\(2 \cdot \measuredangle ADC \equiv \measuredangle AOC,\)
de ahí el resultado.
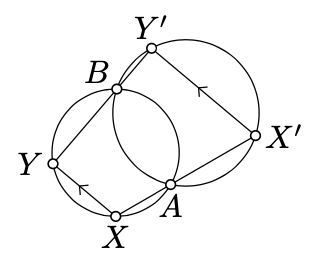
Dejar\(\Gamma\) y\(\Gamma'\) ser dos círculos que se cruzan en dos puntos distintos:\(A\) y\(B\). Asumir\([XY]\) y\([X'Y']\) son los acordes de\(\Gamma\) y\(\Gamma'\) respectivamente, tal que\(A\) se encuentra entre\(X\) y\(X'\) y\(B\) yace entre\(Y\) y\(Y'\). \((XY) \parallel (X'Y')\)Demuéstralo.
- Pista
-
Aplicar Corolario\(\PageIndex{2}\) dos veces para\(\square ABYX\)\(\square ABY'X'\) y utilizar la propiedad transversal (Teorema 7.3.1).


