10.3: Plano inversivo y círculos
- Page ID
- 114448
Dejar\(\Omega\) ser un círculo con el centro\(O\) y el radio r. considerar la inversión en\(\Omega\).
Recordemos que la inversa de\(O\) es indefinida. Para hacer frente a este problema es útil agregar al plano un punto extra; se llamará el punto en el infinito; lo denotaremos como\(\infty\). Podemos suponer que ∞ es inverso de\(O\) y al revés.
El plano euclidiano con un punto agregado en el infinito se llama el plano inversivo.
Siempre asumiremos que cualquier línea y media línea contiene\(\infty\).
Recordemos que circlina, significa círculo o línea. Por lo tanto podemos decir “si una circlina contiene\(\infty\), entonces es una línea” o “una circlina que no contiene\(\infty\) es un círculo”.
Obsérvese que según el Teorema 8.1.1, para cualquiera\(\triangle ABC\) hay una circlina única que pasa a través\(A, B\), y\(C\) (si\(\triangle ABC\) es degenerado, entonces esta es una línea y si no es un círculo).
En el plano inversivo, la inversa de una circlina es una circlina.
- Prueba
-
Supongamos que\(O\) denota el centro de la inversión y\(r\) su radio.
\(\Gamma\)Déjese ser una circlina. Elija tres puntos distintos\(A,B\), y\(C\) en\(\Gamma\). (Si no\(\triangle ABC\) es degenerado, entonces\(\Gamma\) es el circuncírculo de\(\triangle ABC\); si\(\triangle ABC\) es degenerado, entonces\(\Gamma\) es la línea que pasa a través de\(A, B\), y\(C\).)
Dejar\(A', B'\), y\(C'\) denotar las inversas de\(A, B\), y\(C\) respectivamente. Deja\(\Gamma'\) ser la circlina que pasa a través\(A', B'\), y\(C'\).
Supongamos que\(D\) es un punto del plano inversivo que es distinto de\(A, C, O\), y\(\infty\). Supongamos que\(D'\) denota la inversa de\(D\).
Por Teorema 10.2.6c,\(D' \in \Gamma'\) si y solo si\(D \in \Gamma\).
Queda por probarlo\(O \in \Gamma \Leftrightarrow \infty \in \Gamma'\) y\(\infty \in \Gamma \Leftrightarrow O \in \Gamma'\). Ya que\(\Gamma\) es la inversa de\(\Gamma'\), es suficiente para demostrar que
\(\infty \in \Gamma \Leftrightarrow O \in \Gamma'.\)
Si\(\infty \in \Gamma\), entonces\(\Gamma\) es una línea; o, equivalentemente, para alguna\(\varepsilon > 0\), la circlina\(\Gamma\) contiene un punto\(P\) con\(OP > r/\varepsilon\). Para la inversión\(P' \in \Gamma'\) de\(P\), tenemos eso\(OP' = r^2/OP < r \cdot \varepsilon\). Es decir, la circlina\(\Gamma'\) contiene puntos arbitrariamente cercanos a ellos\(O\). De ello se deduce que\(O \in \Gamma'\). De la misma manera podemos comprobar lo contrario.
Supongamos que el círculo\(\Gamma'\) es el inverso del círculo\(\Gamma\). Supongamos que\(Q\) denota el centro de\(\Gamma\) y\(Q'\) denota la inversa de\(Q\). Demostrar que no\(Q'\) es el centro de\(\Gamma'\).
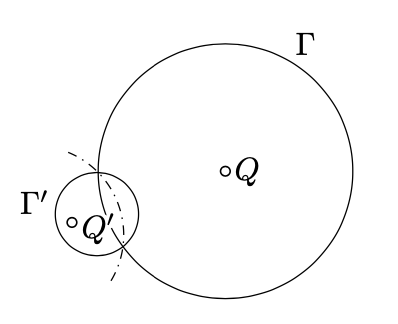
- Pista
-
Primero demuestre que para cualquiera\(r>0\) y para cualquier número real\(x,y\) distinto de 0,
\(\dfrac{r^2}{(x + y)/2} = (\dfrac{r^2}{x} + \dfrac{r^2}{y})/2\)
si y sólo si\(x = y\).
Supongamos que\(\ell\) denota la línea que pasa a través\(Q\)\(Q'\),, y el centro de la inversión\(O\). Elija una isometría\(\ell \to \mathbb{R}\) que envíe\(O\) a 0; asuma que\(x, y \in \mathbb{R}\) son los valores de\(\ell\) para los dos puntos de intersección\(\ell \cap \Gamma\); tenga en cuenta que\(x \ne y\). Supongamos que\(r\) es el radio del círculo de inversión. Entonces el lado izquierdo de arriba es la coordenada de\(Q'\) y el lado derecho es la coordenada del centro de\(\Gamma'\).
Supongamos que una circunherramienta es una herramienta de construcción geométrica que produce una circlina que pasa a través de tres puntos dados.
Demostrar que con solo una circunherramienta, es imposible construir el centro de un círculo dado.
- Pista
-
Se da una solución en la Sección 19.4.
Mostrar que para cualquier par de círculos tangentes en el plano inversivo, hay una inversión que los envía a un par de líneas paralelas.
- Pista
-
Aplicar una inversión en un círculo con el centro en el único punto de intersección de los círculos; luego usar Teorema\(\PageIndex{2}\)
Considera la inversión del plano inversivo en el círculo\(\Omega\) con el centro\(O\). Entonces
(a) Una línea que pasa a través\(O\) se invierte en sí misma.
(b) Una línea que no pasa a través\(O\) se invierte en un círculo que pasa a través\(O\), y al revés.
(c) Un círculo que no pasa a través\(O\) se invierte en un círculo que no pasa a través\(O\).
- Prueba
-
En la prueba utilizamos Teorema\(\PageIndex{1}\) sin mencionarlo.
(a). Tenga en cuenta que si una línea pasa a través\(O\), contiene ambos\(\infty\) y\(O\). Por lo tanto, su inversa también contiene\(\infty\) y\(O\). En particular, la imagen es una línea que pasa a través\(O\).
b). Como cualquier línea\(\ell\) pasa a través\(\infty\), su imagen\(\ell'\) tiene que contener\(O\). Si la línea no contiene\(O\), entonces\(\ell' \not\ni \infty\); es decir, no\(\ell'\) es una línea. Por lo tanto,\(\ell'\) es un círculo que pasa a través\(O\).
c). Si el círculo\(\Gamma\) no contiene\(O\), entonces su imagen\(\Gamma'\) no contiene\(\infty\). Por lo tanto,\(\Gamma'\) es un círculo. Desde que\(\Gamma \not\ni \infty\) lo conseguimos\(\Gamma' \ni O\). De ahí el resultado.


