10.4: Método de inversión

Última actualización
Guardar como PDF

Page ID: 114465

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Aquí hay una aplicación de inversión, que incluimos como ilustración; no la usaremos más en el libro.

Teorema$\PageIndex{1}$ Ptolemy's identity.

Dejado$ABCD$ ser un cuadriángulo inscrito. Supongamos que los puntos$A,B,C$, y$D$ aparecen en la circlina en el mismo orden. Entonces

$AB \cdot CD + BC \cdot DA = AC \cdot BD.$

Prueba

Supongamos que los puntos se$A,B,C,D$ encuentran en una línea en este orden.

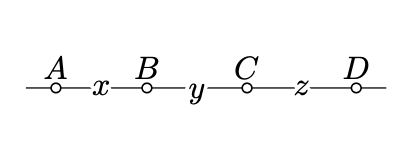
$2021-02-22 10.50.39.png$

Establecer$x = AB$,$y = BC$,$z = CD$. Tenga en cuenta que

$x \cdot z + y \cdot (x + y + z) = (x + y) \cdot (y + z).$

Ya que$AC = x + y$$BD = y + z$,$DA = x + y + z$, y, prueba la identidad.

Queda por considerar el caso cuando el cuadriángulo$ABCD$ está inscrito en un círculo, digamos$\Gamma$.

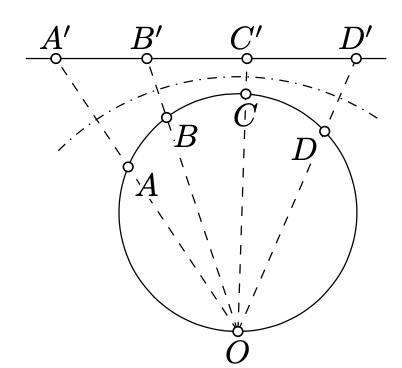
$2021-02-22 10.52.50.png$

La identidad puede ser reescrita como

$\dfrac{AB \cdot DC}{BD \cdot CA} + \dfrac{BC \cdot AD}{CA \cdot DB} = 1.$

En el lado izquierdo tenemos dos ratios cruzados. Según el Teorema 10.3.1a, el lado izquierdo no cambia si aplicamos una inversión a cada punto.

Considera una inversión en un círculo centrado en un punto$O$ que se encuentra$\Gamma$ entre$A$ y$D$. Por Teorema Teorema 10.3.2, esta inversión se mapea$\Gamma$ a una línea. Esto reduce el problema al caso cuando$A, B, C$, y se$D$ encuentran en una línea, que ya se consideró.

En la prueba anterior, reescribimos la identidad de Tolomeo en una forma que es invariante con respecto a la inversión para luego aplicar una inversión que hace evidente la afirmación. La solución del siguiente ejercicio se basa en la misma idea; hay que hacer una elección correcta de inversión.

Ejercicio$\PageIndex{1}$

Supongamos que cuatro círculos son mutuamente tangentes entre sí. Demostrar que cuatro (entre seis) de sus puntos de tangencia se encuentran en una circlina.

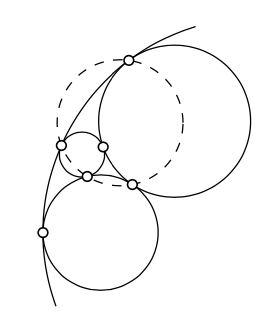
$2021-02-22 10.56.48.png$

Insinuación

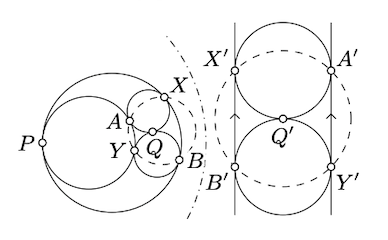
$2021-02-22 10.58.10.png$

Etiquetar los puntos de tangencia por$X, Y , A, B, P$, y$Q$ como en el diagrama. Aplicar una inversión con el centro en$P$. Observe que los dos círculos que tangentes en$P$ se convierten en líneas paralelas y los dos círculos restantes son tangentes entre sí y estas dos líneas paralelas.

Tenga en cuenta que los puntos de tangencia$A'$$B'$$X'$,,, y$Y'$ con las líneas paralelas son vértices de un cuadrado; en particular se encuentran en un círculo. Estos puntos son imágenes de$A, B, X$, y$Y$ bajo la inversión. Por Teorema Teorema 10.3.1, los puntos$A, B, X$, y$Y$ también se encuentran en una circlina.

Ejercicio$\PageIndex{2}$

Supongamos que tres círculos tangentes entre sí y a dos líneas paralelas como se muestra en la imagen.

Mostrar que la línea que pasa a través$A$ y también$B$ es tangente a dos círculos en$A$.

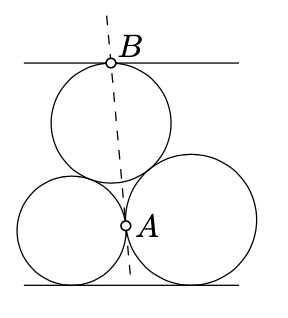
$2021-02-22 10.57.29.png$

Insinuación

Aplicar la inversión en un círculo con centro$A$. El punto$A$ irá al infinito, los dos círculos tangentes en se$A$ convertirán en líneas paralelas y las dos líneas paralelas se convertirán en círculos tangentes en$A$; ver el diagrama.

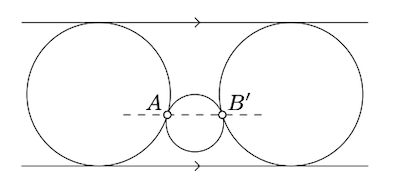
$2021-02-22 11.00.48.png$

Queda por mostrar que la línea discontinua ($AB'$) es paralela a las otras dos líneas.

Teorema\(\PageIndex{1}\) Ptolemy's identity.

Ejercicio\(\PageIndex{1}\)

Ejercicio\(\PageIndex{2}\)