11.2: Dos ángulos de un triángulo

Última actualización
Guardar como PDF

Page ID: 114332

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

En esta sección probaremos una forma más débil del Teorema 7.4.1 que se mantiene en cualquier plano neutro.

Teorema$\PageIndex{1}$

Dejar$\triangle ABC$ ser un triángulo no degenerado en el plano neutro. Entonces

$|\measuredangle CAB| + |\measuredangle ABC| < \pi.$

Tenga en cuenta que según el Teorema 3.3.1, los ángulos$ABC, BCA$, y$CAB$ tienen el mismo signo. Por lo tanto, en el plano euclidiano el teorema sigue inmediatamente del Teorema 7.4.1.

Prueba

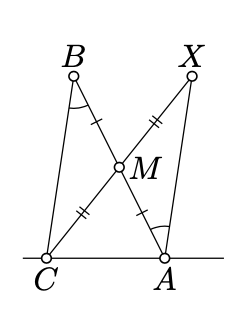
$2021-02-23 9.30.47.png$

Dejar$X$ ser el reflejo de$C$ a través del punto medio$M$ de$[AB]$. Por la Proposición 7.2.1$\measuredangle BAX = \measuredangle ABC$ y por lo tanto

\[\measuredangle CAX \equiv \measuredangle CAB + \measuredangle ABC.\]

Desde$[BM]$ y$[MX]$ no se cruzan$(CA)$, los puntos$B$,$M$, y se$X$ encuentran en el mismo lado de$(CA)$. Por lo tanto los ángulos$CAB$ y$CAX$ tienen el mismo signo. Por el Teorema 3.3.1, los ángulos$CAB, ABC$ tienen el mismo signo; es decir, todos los ángulos en 11.2.1 tienen el mismo signo.

Tenga en cuenta que$\measuredangle CAX \not\equiv \pi$, de lo contrario se$X$ tiraría$(AC)$. Por lo tanto, la identidad 11.2.1 implica que

$|\measuredangle CAB|+|\measuredangle ABC|=|\measuredangle CAX| < \pi.$

Ejercicio$\PageIndex{1}$

Supongamos$A,B,C$, y$D$ son puntos en un plano neutro de tal manera que

$2 \cdot \measuredangle ABC + 2 \cdot \measuredangle BCD \equiv 0.$

$(AB)\parallel (CD)$Demuéstralo.

Tenga en cuenta que no se puede aplicar la propiedad transversal (Teorema 7.3.1)

Pista

Argumentando por contradicción, supongamos$2 \cdot (\measuredangle ABC + \measuredangle BCD) \equiv 0$, pero$(AB) \nparallel (CD)$. Dejar$Z$ ser el punto de intersección de$(AB)$ y$(CD)$.

Tenga en cuenta que$2 \cdot \measuredangle ABC \equiv 2 \cdot \measuredangle ZBC$, y$2 \cdot \measuredangle BCD \equiv 2 \cdot \measuredangle BCZ$.

Aplicar Proposición$\PageIndex{1}$ a$\triangle ZBC$ e intentar llegar a una contradicción.

Ejercicio$\PageIndex{2}$

Demostrar la condición de congruencia de ángulo lateral en la geometría neutra.

Es decir, dejar$ABC$ y$A'B'C'$ ser dos triángulos en un plano neutro; supongamos que eso no$\triangle A'B'C'$ es degenerado. Demuestre que$\triangle ABC \cong \triangle A'B'C'$ si

$AB = A'B'$,$\measuredangle ABC = \pm \measuredangle A'B'C'$ y$\measuredangle BCA = \pm \measuredangle B'C'A'.$

Pista

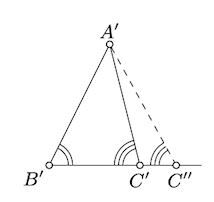
$2021-02-23 10.01.46.png$

Que$C'' \in [B'C')$ sea el punto tal que$B'C'' = BC$.

Tenga en cuenta que por SAS,$\triangle ABC \cong \triangle A'B'C''$. Concluir eso$\measuredangle B'C'A' = \measuredangle B'C''A'$.

Por lo tanto, basta con demostrarlo$C'' = C'$. Si$C' \ne C''$ aplicar Proposición$\PageIndex{1}$ a$\triangle A'C'C''$ e intentar llegar a una contradicción.

Obsérvese que en el plano euclidiano, el ejercicio anterior se desprende de ASA y el teorema sobre la suma de ángulos de un triángulo (Teorema 7.4.1). Sin embargo, el Teorema 7.4.1 no se puede utilizar aquí, ya que su prueba utiliza Axioma V. Posteriormente (Teorema 13.1.1) mostraremos que el Teorema 7.4.1 no se sostiene en un plano neutro.

Ejercicio$\PageIndex{3}$

Supongamos que el punto$D$ se encuentra entre los vértices$A$ y$B$ de$\triangle ABC$ en un plano neutro. Demostrar que

$CD < CA$o$CD < CB$.

Pista

Utilice el Ejercicio 5.2.2 y la Proposición$\PageIndex{1}$.

Alternativamente, utilice el mismo argumento que en la solución del Ejercicio 5.6.1.

Teorema\(\PageIndex{1}\)

Ejercicio\(\PageIndex{1}\)

Ejercicio\(\PageIndex{2}\)

Ejercicio\(\PageIndex{3}\)