11.1: Plano neutro
- Page ID
- 114324
Eliminemos el Axioma V de nuestro sistema axiomático. De esta manera definimos un nuevo objeto llamado plano neutro o plano absoluto. (En un plano neutro, el Axioma V puede mantenerse o no).
Claramente, cualquier teorema en geometría neutra se sostiene en la geometría euclidiana. Es decir, el plano euclidiano es un ejemplo de plano neutro. En el siguiente capítulo vamos a construir un ejemplo de un plano neutro que no es euclidiana.
En este libro se utilizó el Axioma V a partir del Capítulo 6. Por lo tanto, todas las declaraciones antes se mantienen en geometría neutra.
Hace que todos los resultados discutidos sobre medios planos, signos de ángulos, condiciones de congruencia, líneas perpendiculares y reflexiones sean verdaderos en geometría neutra.
Demos un ejemplo de un teorema en geometría neutra que admite una prueba más simple en geometría euclidiana.
Supongamos que triángulo\(ABC\) y\(A'B'C'\) tienen ángulos rectos en\(C\) y\(C'\) respectivamente,\(AB = A'B'\) y\(AC = A'C'\). Entonces\(\triangle ABC \cong \triangle A'B'C'\).
- Prueba
-
Prueba euclidiana. Por el teorema de Pitágoras\(BC = B'C'\). Entonces el enunciado se desprende de la condición de congruencia SSS.
La prueba del teorema de Pitágoras utilizó propiedades de triángulos similares, que a su vez utilizaron Axioma V. Por lo tanto, esta prueba no funciona en un plano neutro.
Prueba neutra. Supongamos que\(D\) denota el reflejo de\(A\) lo ancho\((BC)\) y\(D'\) denota el reflejo de\(A'\) lo ancho\((B'C')\). Tenga en cuenta que
\(AD = 2 \cdot AC = 2 \cdot A'C' = A'D'\),\(BD = BA = B'A' = B'D'.\)
Por condición de congruencia SSS (Teorema 4.4.1), obtenemos eso\(\triangle ABD \cong \triangle A'B'D'\).
La declaración sigue, ya que\(C\) es el punto medio de\([AD]\) y\(C'\) es el punto medio de\([A'D']\).
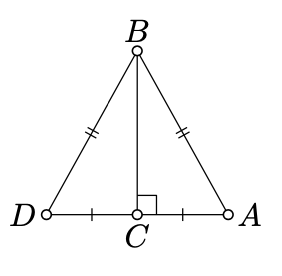
Dar un comprobante del Ejercicio 8.7.1 que funcione en el plano neutro.
- Sugerencia
-
Supongamos que\(D\) denota el punto medio de\([BC]\). Supongamos que\((AD)\) es el ángulo bisectriz en\(A\).
\(A' \in [AD)\)Sea el punto distinto de\(A\) tal que\(AD = A'D\). Tenga en cuenta que\(\triangle CAD \cong \triangle BA'D\). En particular,\(\measuredangle BAA' = \measuredangle AA'B\). Queda por aplicar el Teorema 4.3.1 para\(\triangle ABA'\).
Dejado\(ABCD\) ser un cuadriángulo inscrito en el plano neutro. Demostrar que
\(\measuredangle ABC + \measuredangle CDA \equiv \measuredangle BCD + \measuredangle DAB.\)
- Sugerencia
-
El enunciado es evidente si\(A, B, C\), y\(D\) se encuentran en una línea. En el caso restante, supongamos que\(O\) denota el circuncentro. Aplicar teorema sobre triángulo isósceles (Teorema 4.3.1) a los triángulos\(AOB, BOC, COD, DOA\).
(Obsérvese que en el plano euclidiano la declaración se desprende del Corolario 9.3.2 y del Ejercicio 7.4.5, pero no se pueden usar estas declaraciones en el plano neutro).
Obsérvese que no se puede utilizar el Corolario 9.3.2 para resolver el ejercicio anterior, ya que utiliza el Teorema 9.1.1 y el Teorema 9.2.1, que a su vez usa el Teorema 7.4.1.