11.3: Tres ángulos de triángulo

Última actualización
Guardar como PDF

Page ID: 114340

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Proposición$\PageIndex{1}$

Dejar$\triangle ABC$ y$\triangle A'B'C'$ ser dos triángulos en el plano neutro tal que$AC = A'C'$ y$BC = B'C'$. Entonces

$AB < A'B'$si y sólo si$|\measuredangle ACB| < |\measuredangle A'C'B'|$.

Prueba

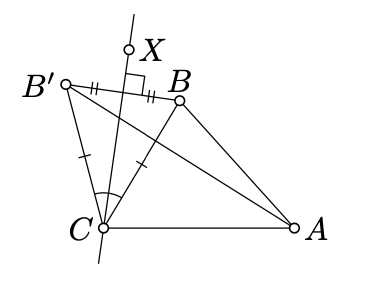
$2021-02-23 10.14.09.png$

Sin pérdida de generalidad, podemos suponer que$A = A'$,$C = C'$, y$\measuredangle ACB$,$\measuredangle ACB' \ge 0$. En este caso tenemos que demostrar que

$AB < AB' \Leftrightarrow \measuredangle ACB < \measuredangle ACB'.$

Elige un punto$X$ para que

$\measuredangle ACX = \dfrac{1}{2} \cdot (\measuredangle ACB + \measuredangle ACB').$

Tenga en cuenta que

$(CX)$bisectos$\angle BCB'$.
$(CX)$es la bisectriz perpendicular de$[BB']$.
$A$y$B$ se encuentran en el mismo lado de$(CX)$ si y solo si

$\measuredangle ACB < \measuredangle ACB'$.

Del Ejercicio 5.2.1,$A$ y$B$ acostarse del mismo lado de$(CX)$ si y solo si$AB < AB'$. De ahí el resultado.

Teorema$\PageIndex{1}$

Dejar$\triangle ABC$ ser un triángulo en el plano neutro. Entonces

$|\measuredangle ABC| + |\measuredangle BCA| + |\measuredangle CAB| \le \pi.$

La siguiente prueba se debe a Legendre [12], las pruebas de los ganadores se debieron a Saccheri [16] y Lambert [11].

Prueba

Set

$\begin{array} {rclcrclcrcl} {a} & = & {BC,} & \ \ \ \ \ & {b} & = & {CA,} & \ \ \ \ \ & {c} & = & {AB,} \\ {\alpha} & = & {\measuredangle CAB,} & \ \ \ \ \ & {\beta} & = & {\measuredangle ABC,} & \ \ \ \ \ & {\gamma} & = & {\measuredangle BCA.} \end{array}$

Sin pérdida de generalidad, podemos suponer eso$\alpha, \beta, \gamma \ge 0$.

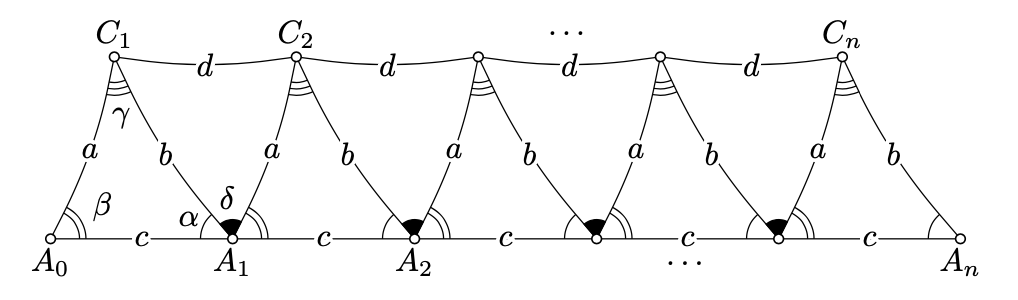
$2021-02-23 10.29.47.png$

Arreglar un entero positivo$n$. Considera los puntos$A_0, A_1, ..., A_n$ en la media línea$[BA)$, tal que$BA_i = i \cdot c$ para cada uno$i$. (En particular,$A_0 = B$ y$A_1 = A$.) Construyamos los puntos$C_1, C_2, ..., C_n$, para eso$\measuredangle A_iA_{i-1}C_i = \beta$ y$A_{i-1} C_i = a$ para cada uno$i$.

Por SAS, hemos construido n triángulos congruentes

$\triangle ABC = \triangle A_1A_0C_1 \cong \triangle A_2A_1C_2 \cong ... \cong \triangle A_nA_{n-1} C_n.$

Establecer$d = C_1C_2$ y$\delta = \measuredangle C_2A_1C_1$. Tenga en cuenta que

\[\alpha + \beta + \delta = \pi.\]

Por la Proposición 11.2.1, lo conseguimos$\Delta \ge 0$.

Por construcción

$\triangle A_1C_1C_2 \cong \triangle A_2C_2C_3 \cong ... \cong \triangle A_{n - 1} C_{n - 1} C_n.$

En particular,$C_i C_{i + 1} = d$ para cada uno$i$.

Por la aplicación repetida de la desigualdad triangular, obtenemos que

$\begin{array} {rcl} {n \cdot c} & = & {A_0A_n \le} \\ {} & \le & {A_0 C_1 + C_1 C_2 + \cdots + C_{n - 1} C_n + C_n A_n =} \\ {} & = & {a + (n - 1) \cdot d + b.} \end{array}$

En particular,

$c \le d + \dfrac{1}{n} \cdot (a + b - d).$

Dado que$n$ es un entero positivo arbitrario, este último implica$c \le d$. Por Proposición$\PageIndex{1}$, es equivalente a

$\gamma \le \delta.$

A partir del 11.3.1, sigue el teorema.

Ejercicio$\PageIndex{1}$

Dejar$ABCD$ ser un cuadriángulo en el plano neutro. Supongamos que los ángulos$DAB$ y$ABC$ son correctos. $AB \le CD$Demuéstralo.

Pista

Set$a = AB, b = BC, c = CD$, y$d = DA$; nned para mostrar eso$c \ge a$.

Imita la prueba de Teorema$\PageIndex{1}$ para la barda mostrada hecha a partir de copias de cuadriángulo$ABCD$.

Proposición\(\PageIndex{1}\)

Teorema\(\PageIndex{1}\)

Ejercicio\(\PageIndex{1}\)