Search

Text Color

Margin Size

Font Type

Enable Dyslexic Font

11.4: Defecto

Última actualización

30 oct 2022
Guardar como PDF
- 11.3: Tres ángulos de triángulo
- 11.5: Cómo probar que algo no se puede probar

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

El defecto del triángulo $\triangle ABC$ se define como

$\text{defect} (\triangle ABC) := \pi - |\measuredangle ABC| - |\measuredangle BCA| - |\measuredangle CAB|.$

Obsérvese que el Teorema 11.3.1 establece que el defecto de cualquier triángulo en un plano neutro tiene que ser no negativo. Según el Teorema 7.4.1, cualquier triángulo en el plano euclidiano tiene defecto cero.

Ejercicio $\PageIndex{1}$

Dejar $\triangle ABC$ ser un triángulo no degenerado en el plano neutro. Asumir $D$ mentiras entre $A$ y $B$ . Demostrar que

$\text{defect} (\triangle ABC) = \text{defect} (\triangle ADC) + \text{defect} (\triangle DBC).$

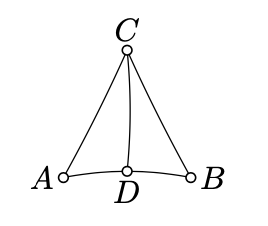
$2021-02-23 10.49.18.png$

Pista: Tenga en cuenta que $|\measuredangle ADC| + |\measuredangle CDB| = \pi$ . A continuación, aplicar la definición del defecto.

Ejercicio $\PageIndex{2}$

Dejar $ABC$ ser un triángulo no degenerado en el plano neutro. Supongamos que $X$ es el reflejo de $C$ a través del punto medio $M$ de $[AB]$ . Demostrar que

$\text{defect} (\triangle ABC) = \text{defect} (\triangle AXC).$

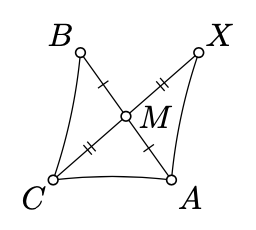
$2021-02-23 10.50.45.png$

Pista: $\triangle AMX \cong \triangle BMC$ Demuéstralo. Aplicar Ejercicio $\PageIndex{1}$ a $\triangle ABC$ y $\triangle AXC$ .

Ejercicio $\PageIndex{3}$

Supongamos que $ABCD$ es un rectángulo en un plano neutro; es decir, $ABCD$ es un cuadriángulo con todos los ángulos rectos. $AB = CD$ Demuéstralo.

Pista

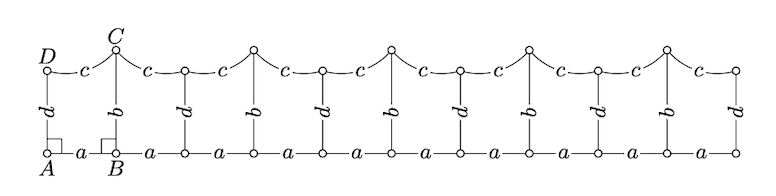
$2021-02-23 10.55.37.png$

$B$ Demuéstralo y $D$ acuéstate en los lados opuestos de $(AC)$ . Concluir que

$\text{defect} (\triangle ABC) + \text{defect} (\triangle CDA) = 0.$

Aplicar Teorema $\PageIndex{1}$ para demostrar que

$\text{defect} (\triangle ABC) = \text{defect} (\triangle CDA = 0$

Úselo para mostrar eso $\meauredangle CAB = \measuredangle ACD$ y $\measuredangle ACB = \measuredangle CAD$ . Por ASA, $\triangle ABC \cong \triangle CDA$ , y, en particular, $AB =CD$ .

(Alternativamente, puede aplicar el Ejercicio 11.3.1)

Ejercicio Avanzado $\PageIndex{4}$

Mostrar que si un plano neutro tiene un rectángulo, entonces todos sus triángulos tienen defecto cero.

Ejercicio11.4.1\PageIndex{1}

Ejercicio11.4.2\PageIndex{2}

Ejercicio11.4.3\PageIndex{3}

Ejercicio Avanzado11.4.4\PageIndex{4}

Support Center

How can we help?

Ejercicio $\PageIndex{1}$

Ejercicio $\PageIndex{2}$

Ejercicio $\PageIndex{3}$

Ejercicio Avanzado $\PageIndex{4}$