13.3: Círculos, Horociclos y Equidistantes

Tenga en cuenta que según Lemma 12.3.4, cualquier círculo h es un círculo euclidiano que se encuentra completamente en el plano h. Además, cualquier línea h es una intersección del plano h con el círculo perpendicular al absoluto. En esta sección describiremos el significado geométrico h de las intersecciones de los otros círculos con el plano h.

Verás que todas estas intersecciones tienen una forma perfectamente redonda en el plano h. Se puede pensar en estas curvas como trayectorias de un automóvil con una posición fija del volante. En el plano euclidiano, de esta manera corres a lo largo de un círculo o a lo largo de una línea. En el plano hiperbólico, la imagen es diferente. Si giras el volante hacia el extremo derecho, correrás a lo largo de un círculo. Si lo giras menos, en cierta posición de la rueda, nunca volverás al mismo punto, pero el camino será diferente a la línea. Si giras un poco más la rueda, comienzas a correr por un camino que se mantiene a cierta distancia fija de una línea h.

Equidistantes de líneas h. Considera el plano h con el absoluto\(\Omega\). Supongamos que un círculo\(\Gamma\) se cruza\(\Omega\) en dos puntos distintos,\(A\) y\(B\). Supongamos que\(g\) denota la intersección de\(\Gamma\) con el plano h.

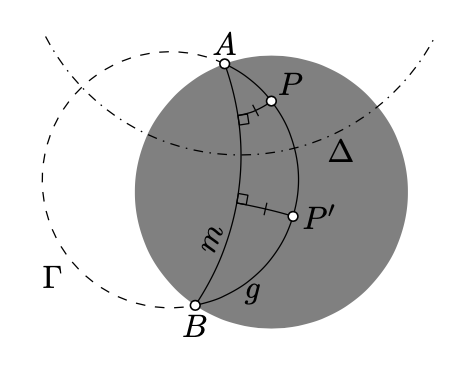
Dibujemos una línea h\(m\) con los puntos ideales\(A\) y\(B\). De acuerdo con el Ejercicio 12.1.1,\(m\) se define de manera única.

Considera cualquier línea h\(\ell\) perpendicular a\(m\); deja\(\Delta\) ser el círculo que contiene\(\ell\).

Tenga en cuenta que\(\Delta\perp \Gamma\). En efecto, según el Corolario 10.5.1,\(m\) e\(\Omega\) invertir a sí mismos en\(\Delta\). De ello se deduce que\(A\) es la inversa de\(B\) in\(\Delta\). Por último, por Corolario 10.5.2, lo conseguimos\(\Delta\perp \Gamma\).

Por lo tanto, la inversión en\(\Delta\) envía\(m\) tanto como\(g\) a sí mismos. Para dos puntos cualesquiera\(P',P\in g\) hay una elección de\(\ell\) y\(\Delta\) como arriba tal que\(P'\) es la inversa de\(P\) in\(\Delta\). Por la observación principal (Teorema 12.3.1) la inversión en\(\Delta\) es un movimiento del plano h. Por lo tanto, todos los puntos de\(g\) mentira a la misma distancia de\(m\).

En otras palabras,\(g\) es el conjunto de puntos que se encuentran en una distancia h fija y en el mismo lado de\(m\).

Tal curva\(g\) se llama equidistante a la línea h\(m\). En geometría euclidiana, lo equidistante de una línea es una línea; aparentemente en geometría hiperbólica la imagen es diferente.

Horociclos. Si el círculo\(\Gamma\) toca el absoluto desde adentro en un punto\(A\), entonces el complemento\(h=\Gamma\backslash\{A\}\) se encuentra en el plano h. Este conjunto se llama horociclo. También tiene una forma perfectamente redonda en el sentido descrito anteriormente.

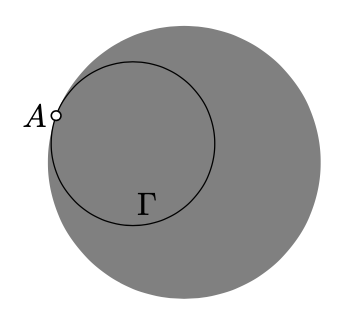
La forma de un horociclo es entre formas de círculos y equidistantes a líneas h. Un horociclo podría considerarse como un límite de círculos a través de un punto fijo con los centros corriendo hasta el infinito a lo largo de una línea. El mismo horociclo es un límite de equidistantes a través de un punto fijo a la secuencia de líneas h que corre hasta el infinito.

Dado que tres puntos cualesquiera se encuentran en una circlina, tenemos que cualquier triángulo h no degenerado está inscrito en un círculo h, un horociclo o un equidistante.

Ejercicio\(\PageIndex{1}\)

Encuentra la pata de un triángulo h rectángulo isósceles inscrito en un horociclo.

Sugerencia

Como es habitual, suponemos que el absoluto es un círculo unitario.

Dejar\(PQR\) ser un triángulo hiperbólico con un ángulo recto en\(Q\), tal que\(PQ_h = QR_h\) y los vértices\(P, Q\), y se\(R\) encuentran en un horociclo.

Sin pérdida de generalidad, podemos suponer que\(Q\) es el centro de lo absoluto. En este caso\(\measuredangle_h PQR = \measuredangle PQR = \pm \dfrac{\pi}{2}\) y\(PQ = QR\).

Tenga en cuenta que el círculo euclidiano pasa a través\(P, Q\), y\(R\) es tangente a lo absoluto. Concluir eso\(PQ = \dfrac{1}{\sqrt{2}}\). Aplicar Lemma 12.3.2 para encontrar\(PQ_h\).