13.4: Triángulos hiperbólicos

Teorema\(\PageIndex{1}\)

Cualquier triángulo hiperbólico no degenerado tiene un defecto positivo.

Prueba

Arreglar un triángulo h\(ABC\). Según el Teorema 11.3.1,

\[\text{defect}(\triangle_hABC)\ge 0\]

Queda por demostrar que en el caso de la igualdad,\(\triangle_hABC\) degenera.

Sin pérdida de generalidad, podemos suponer que\(A\) es el centro de lo absoluto; en este caso\(\measuredangle_h CAB = \measuredangle CAB\). Sin embargo, podemos suponer que

\(\measuredangle_h CAB\),\(\measuredangle_h ABC\),\(\measuredangle_h BCA\),\( \measuredangle ABC\),\(\measuredangle BCA \ge 0.\)

\(D\)Sea un punto arbitrario en\([CB]_h\) distinto de\(B\) y\(C\). De la Proposición 9.6.1, tenemos

\(\measuredangle ABC-\measuredangle_h ABC \equiv \pi-\measuredangle CDB \equiv \measuredangle BCA-\measuredangle_h BCA.\)

Del Ejercicio 7.4.2, obtenemos eso

Por lo tanto, si tenemos igualdad en 13.4.1, entonces\(\measuredangle CDB=\pi\). En particular, el segmento h\([BC]_h\) coincide con el segmento euclidiano\([BC]\). Por el Ejercicio 12.1.3, este último sólo puede ocurrir si la línea h\((BC)_h\) pasa por el centro del absoluto (\(A\)); es decir, si\(\triangle_hABC\) degenera.

El siguiente teorema afirma, en particular, que los triángulos hiperbólicos no degenerados son congruentes si sus ángulos correspondientes son iguales. En particular, en geometría hiperbólica, triángulos similares tienen que ser congruentes.

Teorema\(\PageIndex{2}\) AAA congruence condition

Dos triángulos h no degenerados\(ABC\) y\(A'B'C'\) son congruentes si\(\measuredangle_hABC = \pm \measuredangle_hA'B'C'\),\(\measuredangle_hBCA = \pm \measuredangle_h B'C'A'\) y\(\measuredangle_hCAB = \pm \measuredangle_hC'A'B'\).

Prueba

Tenga en cuenta que si\(AB_h=A'B'_h\), entonces el teorema se desprende de ASA.

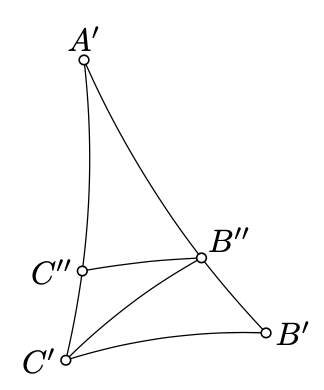
Asumir lo contrario. Sin pérdida de generalidad, podemos suponer eso\(AB_h<A'B'_h\). Por lo tanto, podemos elegir el punto de\(B''\in [A'B']_h\) tal manera que\(A'B''_h=AB_h\).

Elija una media línea h\([B''X)\) para que

\(\measuredangle_h A'B''X=\measuredangle_h A'B'C'.\)

De acuerdo con el Ejercicio 11.5,\((B''X)_h\parallel(B'C')_h\).

Por el teorema de Pasch (Teorema 3.12),\((B''X)_h\) se cruza\([A'C']_h\). Supongamos que\(C''\) denota el punto de intersección.

De acuerdo con ASA,\(\triangle_h ABC\cong\triangle_h A'B''C''\); en particular,

\[\text{defect}(\triangle_h ABC)=\text{defect}(\triangle_h A'B''C'').\]

Aplicando el Ejercicio 11.11 dos veces, lo conseguimos

\[\begin{array} {rcl} {\text{defect} (\triangle_h A'B'C')} & = & {\text{defect} (\triangle_h A'B''C'') +} \\ {} & + & {\text{defect}(\triangle_h B''C''C') + \text{defect} (\triangle_h B''C'B').} \end{array}\]

Por Teorema 13.7, todos los defectos tienen que ser positivos. Por lo tanto

\(\text{defect} (\triangle_h A'B'C') > \text{defect} (\triangle_h ABC).\)

Por otra parte,

\(\begin{array} {rcl} {\text{defect} (\triangle_h A'B'C')} & = & {|\measuredangle_h A'B'C'| + |\measuredangle_h B'C'A'| + |\measuredangle_h C'A'B'| =} \\ {} & = & {|\measuredangle_h ABC| + |\measuredangle_BCA| + |\measuredangle_h CAB|} \\ {} & = & {\text{defect} (\triangle_h ABC)} \end{array}\)

— una contradicción.

Recordemos que una bijección de un plano h a sí mismo se llama preservación de ángulo si

\(\measuredangle_h ABC= \measuredangle_h A'B'C'\)

para cualquiera\(\triangle_h ABC\) y su imagen\(\triangle_h A'B'C'\).

Ejercicio\(\PageIndex{1}\)

Demostrar que cualquier transformación que conserve el ángulo del plano h es un movimiento.

Pista

Aplicar condición de congruencia AAA (Teorema\(\PageIndex{2}\))