13.5: Interpretación conforme
- Page ID
- 114342
Demos otra interpretación de la distancia h.
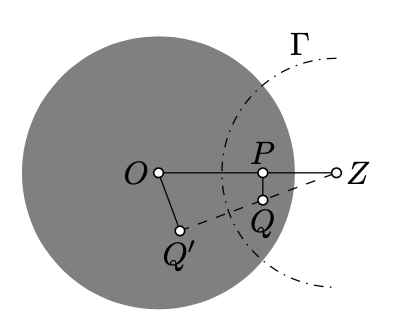
Considera el plano h con el círculo unitario centrado en\(O\) como el absoluto. Fijar un punto\(P\) y dejar\(Q\) ser otro punto en el plano h. Establecer\(x = PQ\) y\(y = PQ_h\). Entonces
\[\lim_{x\to 0} \dfrac{y}{x} = \dfrac{2}{1-OP^2}.\]
La fórmula anterior nos dice que la distancia h desde\(P\) un punto cercano\(Q\) es casi proporcional a la distancia euclidiana con el coeficiente\(\dfrac{2}{1-OP^2}\). El valor\(\lambda(P)=\dfrac{2}{1-OP^2}\) se denomina factor de conformación de la métrica h.
El valor\(\dfrac{1}{\lambda(P)}=\dfrac{1}{2} \cdot (1-OP^2)\) puede interpretarse como el límite de velocidad en el punto dado\(P\). En este caso la distancia h es el tiempo mínimo necesario para viajar de un punto del plano h a otro punto.
- Prueba
-
Si\(P=O\), entonces según Lema 12.3.2
\[\dfrac{y}{x}=\dfrac{\ln \dfrac{1+x}{1-x}}{x}\to 2\]
como\(x\to0\).
Si\(P\ne O\), let\(Z\) denota la inversa de\(P\) en el absoluto. Supongamos que\(\Gamma\) denota el círculo con el centro\(Z\) perpendicular al absoluto.
Según la observación principal (Teorema 12.3.1) y Lema 12.3.1, la inversión en\(\Gamma\) es un movimiento del plano h\(P\) al que envía\(O\). En particular, si\(Q'\) denota la inversa de\(Q\) in\(\Gamma\), entonces\(OQ'_h=PQ_h\).
Set\(x'=OQ'\). Según Lemma 10.1.1,
\(\dfrac{x'}{x}=\dfrac{OZ}{ZQ}.\)
Ya que\(Z\) es lo inverso de\(P\) en lo absoluto, tenemos eso\(PO\cdot OZ=1\). Por lo tanto,
como\(x \to 0\).
Según 13.5.1,\(\dfrac{y}{x'} \to 2\) como\(x' \to 0\). Por lo tanto
como\(x \to 0\).
Aquí hay una aplicación del lema anterior.
La circunferencia de un círculo h del radio h\(r\) es
\(2 \cdot \pi \cdot \sinh r,\)
donde\(\sinh r\) denota el seno hiperbólico de\(r\); es decir,
\(\sinh r := \dfrac{e^r-e^{-r}}{2}.\)
Antes de proceder con la prueba, hablemos del mismo problema en el plano euclidiana.
La circunferencia de un círculo en el plano euclidiano se puede definir como el límite de perímetros de\(n\) -gones regulares inscritos en el círculo como\(n \to \infty\).
A saber, arreglemos\(r>0\). Dado un entero positivo\(n\), considere\(\triangle AOB\) tal que\(\measuredangle AOB=\dfrac{2\cdot\pi}{n}\) y\(OA=OB=r\). Set\(x_n=AB\). Tenga en cuenta que\(x_n\) es el lado de un\(n\) -gon regular inscrito en el círculo de radio\(r\). Por lo tanto, el perímetro del\(n\) -gon es\(n\cdot x_n\).
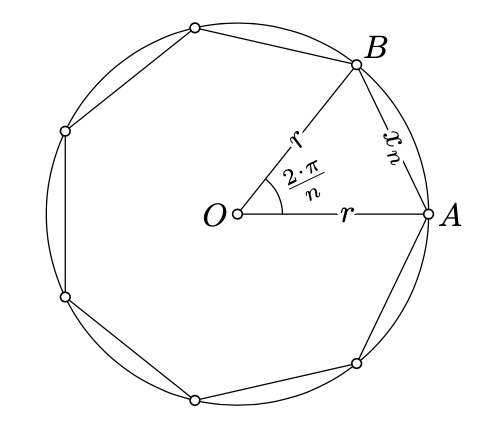
La circunferencia del círculo con el radio\(r\) podría definirse como el límite
\[\lim_{n\to\infty} n\cdot x_n=2\cdot\pi\cdot r.\]
(Este límite puede tomarse como la definición de\(\pi\).)
En la siguiente prueba, repetimos la misma construcción en el plano h.
- Prueba
-
Sin pérdida de generalidad, podemos suponer que el centro\(O\) del círculo es el centro de lo absoluto.
Por Lema 12.3.2, el círculo h con el radio h\(r\) es el círculo euclidiano con el centro\(O\) y el radio
\(a=\dfrac{e^r-1}{e^r+1}.\)
Dejar\(x_n\) y\(y_n\) denotar las longitudes laterales de los\(n\) -gones regulares inscritos en el círculo en el plano euclidiano e hiperbólico respectivamente.
Tenga en cuenta que\(x_n\to0\) como\(n\to\infty\). Por Lemma\(\PageIndecx{1}\),
\(\lim_{n\to\infty} \dfrac{y_n}{x_n} = \dfrac{2}{1-a^2}.\)
Aplicando 13.5.2, obtenemos que la circunferencia del círculo h se puede encontrar de la siguiente manera:
\(\begin{array} {rcl} {\lim_{n \to \infty} n \cdot y_n} & = & {\dfrac{2}{1 - a^2} \cdot \lim_{n \to \infty} n \cdot x_n =} \\ {} & = & {\dfrac{4 \cdot \pi \cdot a}{1 - a^2} =} \\ {} & = & {\dfrac{4 \cdot \pi \cdot (\dfrac{e^r - 1}{e^r + 1})}{1 - (\dfrac{e^r - 1}{e^r + 1})^2} =} \\ {} & = & {2 \cdot \pi \cdot \dfrac{e^r - e^{-r}}{2} =} \\ {} & = & {2 \cdot \pi \cdot \sinh r.} \end{array}\)
Dejar\(\circum_h(r)\) denotar la circunferencia del círculo h del radio h\(r\). Demostrar que
\ (\\ texto {circum} _h (r+1) >2\ cdot\ texto {circum} _h (r)\])
para todos\(r>0\).
- Pista
-
Aplicar Proposición\(\PageIndex{1}\). Usa eso\(e > 2\) y en particular la función\(r \mapsto e^{-r}\) es decreciente.


