14.3: Teorema Fundamental de la Geometría Afín

Última actualización
Guardar como PDF

Page ID: 114685

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Además asumimos el conocimiento del álgebra vectorial, es decir, la multiplicación por un número real, la suma y la regla del paralelogramo.

Ejercicio$\PageIndex{1}$

Mostrar que las transformaciones afín mapean paralelogramos a paralelogramos. Concluir que si$P\mapsto P'$ es una transformación afín, entonces

$\overrightarrow{XY}=\overrightarrow{AB}$,$\text{if and only if}$$\overrightarrow{X'Y'} =\overrightarrow{A'B'}.$

Pista: Aplicar dos veces Ejercicio 14.1.1 y la regla del paralelogramo. (Tenga en cuenta que el caso si$A, B, X$, y$Y$ son colineales requiere trabajo extra.)

Proposición$\PageIndex{1}$

$P \mapsto P'$Sea una transformación afín del plano euclidiano. Entonces, para cualquier triple de puntos$O$$X$,$P$,, tenemos

\[\overrightarrow{OP}=t \cdot \overrightarrow{OX} \ \ \ \ \text{if and only if}\ \ \ \ \overrightarrow{O'P'} =t \cdot \overrightarrow{O'X'}.\]

Prueba

Observe que las transformaciones afín descritas en el Ejercicio 14.1.2 así como todos los movimientos satisfacen la condición 14.3.1. Por lo tanto, una transformación afín dada$P \mapsto P'$ satisface 14.3.1 si y solo si su composición con movimientos y escalamientos satisface 14.3.1.

Aplicando esta observación, podemos reducir el problema a su caso parcial. Es decir, podemos suponer que$O'=O$,$X'=X$, el punto$O$ es el origen de un sistema de coordenadas, y$X$ tiene coordenadas$(1,0)$.

En este caso,$\overrightarrow{OP}=t\cdot \overrightarrow{OX}$ si y sólo si$P=(t,0)$. Desde$O$ y$X$ son fijos, la transformación mapea el$x$ eje -a sí mismo. Es decir,$P'=(f(t),0)$ para alguna función$t\mapsto f(t)$, o, equivalentemente,$\overrightarrow{O'P'}=f(t)\cdot \overrightarrow{O'X'}$. Queda por demostrar que

\[f(t)=t \]

para cualquier$t$.

Desde$O'=O$ y$X'=X$, obtenemos eso$f(0)=0$ y$f(1)=1$. Además, de acuerdo con el Ejercicio 14.2.2, tenemos eso$f(x\cdot y)=f(x)\cdot f(y)$ y$f(x+y)=f(x)+f(y)$ para cualquiera$x,y \in \mathbb{R}$. Por el lema algebraico (probado a continuación, ver Lema 14.4.1), estas condiciones implican 14.3.2.

Teorema$\PageIndex{1}$ Fundamental theorem of affine geometry

Supongamos que una transformación afín mapea un triángulo no degenerado$OXY$ a un triángulo$O'X'Y'$. Entonces no$\triangle O'X'Y'$ es degenerado, y

$\overrightarrow{OP}=x \cdot \overrightarrow{OX} + y \cdot \overrightarrow{OY} \ \ \ \text{if and only if}\ \ \ \ \overrightarrow{O'P'} =x\cdot\overrightarrow{O'X'}+y\cdot\overrightarrow{O'Y'}.$

Prueba

Dado que una transformación afín mapea líneas a líneas, el triángulo no$O'X'Y'$ es degenerado.

Si$x=0$ o$y=0$, entonces la segunda declaración se desprende directamente de la proposición. De lo contrario considerar los puntos$V$ y$W$ definidos por

$\overrightarrow{OV} = x \cdot \overrightarrow{OX}, \ \ \ \overrightarrow{OW} = y \cdot \overrightarrow{OY}.$

Por la proposición,

$\overrightarrow{O'V'}=x\cdot\overrightarrow{O'X'}, \ \ \ \overrightarrow{O'W'} =y \cdot \overrightarrow{O'Y'}.$

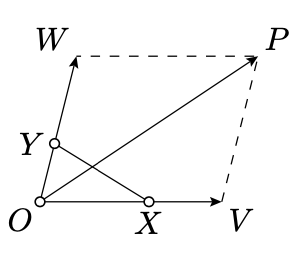
$2021-02-25 10.52.19.png$

Tenga en cuenta que

$\overrightarrow{OP}=\overrightarrow{OV}+\overrightarrow{OW},$

o, equivalentemente,$\square OVPW$ es un paralelogramo. De acuerdo con el Ejercicio 14.1.1, también$\square O'V'P'W'$ es un paralelogramo. Por lo tanto

$\begin{array} {rcl} {\overrightarrow{O'P'}} & = & {\overrightarrow{O'V'} + \overrightarrow{O'W'} =} \\ {} & = & {x \cdot \overrightarrow{O'X'} + y \cdot \overrightarrow{O'Y'}} \end{array}$

Ejercicio$\PageIndex{2}$

Demostrar que cualquier transformación afín es continua.

Pista: Fijar un sistema de coordenadas y aplicar el teorema fundamental de la geometría afín (Teorema$\PageIndex{1}$) para los puntos$O = (0, 0), X = (1, 0)$ y$Y = (0, 1)$.

El siguiente ejercicio proporciona lo contrario al Ejercicio Ejercicio 14.1.2 d).

Ejercicio$\PageIndex{3}$

Demostrar que cualquier transformación afín puede escribirse en coordenadas como

$(x,y)\mapsto(a\cdot x+b\cdot y+r,c\cdot x+d\cdot y+s)$

para constantes$a,b,c,d,r,s$ tales que la matriz$(\begin{smallmatrix}a&b\\c&d\end{smallmatrix})$ sea invertible.

Pista: Fijar un sistema de coordenadas y aplicar el teorema fundamental de la geometría afín (Teorema$\PageIndex{1}$) para los puntos$O = (0, 0), X = (1, 0)$ y$Y = (0, 1)$.

Ejercicio\(\PageIndex{1}\)

Proposición\(\PageIndex{1}\)

Teorema\(\PageIndex{1}\) Fundamental theorem of affine geometry

Ejercicio\(\PageIndex{2}\)

Ejercicio\(\PageIndex{3}\)