15.4: Proyección en perspectiva

Última actualización
Guardar como PDF

Page ID: 114693

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Considera dos planos$\Pi$ y$\Pi'$ en el espacio euclidiano. $O$Sea un punto que no le pertenece ni a$\Pi$ ni$\Pi'$.

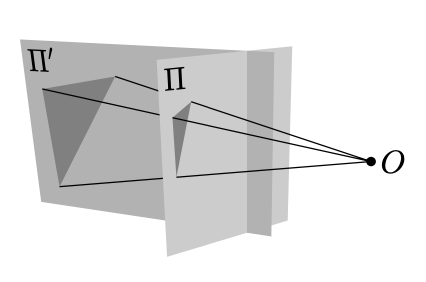
$2021-02-25 2.13.56.png$

Una proyección en perspectiva de$\Pi$ a$\Pi'$ con centro en$O$ mapea un punto$P\in \Pi$ al punto de intersección$P'=\Pi'\cap (OP)$.

En general, la proyección en perspectiva no es una biyección entre los planos. En efecto, si la línea$(OP)$ es paralela a$\Pi'$ (es decir, si$(OP)\cap\Pi'=\emptyset$) entonces la proyección en perspectiva de$P\in \Pi$ es indefinida. También, si es$(OP')\parallel \Pi$ por$P'\in \Pi'$, entonces el punto no$P'$ es una imagen de la proyección en perspectiva.

Por ejemplo, deja$O$ ser el origen del espacio$(x,y,z)$ -coordenada y los planos$\Pi$ y$\Pi'$ están dados por las ecuaciones$z=1$ y$x=1$ respectivamente. Entonces la proyección de perspectiva de$\Pi$ a se$\Pi'$ puede escribir en las coordenadas como

$(x,y,1)\mapsto (1,\dfrac{y}{x},\dfrac{1}{x}).$

De hecho, las coordenadas tienen que ser proporcionales; los puntos$\Pi$ tienen$z$ coordenadas unitarias y los puntos en$\Pi'$ tienen$z$ coordenada unitaria.

La proyección en perspectiva, mapea un plano a otro. Sin embargo, podemos identificar los dos planos fijando un sistema de coordenadas en cada uno. En este caso obtenemos un mapa parcialmente definido desde el plano hacia sí mismo. Mantendremos la transformación de la perspectiva del nombre para dichos mapas.

Para la proyección en perspectiva descrita; podemos obtener el mapa

\[\beta\:(x,y)\mapsto (\dfrac{1}{x},\dfrac{y}{x}).\]

Este mapa no está definido en la línea$x=0$. También los puntos en esta línea no son imágenes de puntos bajo proyección en perspectiva.

Denotar por$\hat \Pi$ y$\hat \Pi'$ las terminaciones proyectivas de$\Pi$ y$\Pi'$ respectivamente. Obsérvese que la proyección en perspectiva es una restricción de composición de las dos biyecciones$\hat \Pi\leftrightarrow\Phi \leftrightarrow\hat \Pi'$ construidas en el apartado anterior. Por la Observación 15.3.1, la proyección en perspectiva puede extenderse a una biyección$\hat \Pi\leftrightarrow\hat \Pi'$ que envía líneas a líneas. (Una historia similar ocurrió con la inversión. Una inversión no se define en su centro; además, el centro no es una inversa de ningún punto. Para hacer frente a este problema pasamos al plano inversivo que es el plano euclidiano extendido por un punto ideal. La misma estrategia funcionó para la proyección de perspectiva$\Pi \to \Pi'$, pero esta vez necesitamos agregar una línea ideal).

Por ejemplo, para definir la extensión de la proyección de perspectiva$\beta$ en 15.4.1, tenemos que observar que

El lápiz de líneas verticales$x=a$ se mapea a sí mismo.
Los puntos ideales definidos por lápiz de líneas$y=m \cdot x+ b$ se mapean al punto$(0,m)$ y al revés — punto$(0, m)$ se mapea al punto ideal definido por el lápiz de líneas$y=m \cdot x+ b$.