15.6: Mover puntos al infinito
- Page ID
- 114707
El teorema 15.5.1 permite tomar cualquier línea en el plano proyectivo y declararla ideal. En otras palabras, podemos elegir un plano afín preferido quitando una línea del plano proyectivo. Esta construcción proporciona un método para resolver problemas en geometría proyectiva que se ilustrará con el siguiente ejemplo clásico:
Teorema de Desargues [thm:desargues] Consideremos tres líneas concurrentes\((AA')\)\((BB')\),, y\((CC')\) en el plano proyectivo real. Set
\(\begin{aligned} X&=(BC)\cap (B'C'),\\ Y&=(CA)\cap (C'A'),\\ Z&=(AB)\cap (A'B').\end{aligned}\)
Entonces los puntos\(X\),\(Y\), y\(Z\) son colineales.
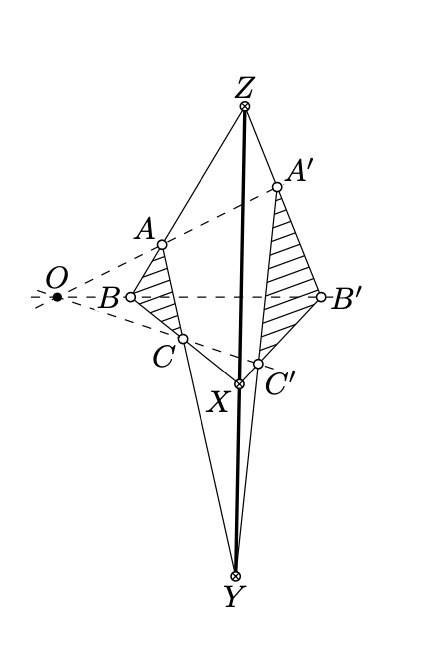
- Prueba
-
Sin pérdida de generalidad, podemos suponer que la línea\((XY)\) es ideal. Si no, aplique una proyección en perspectiva que envíe la línea\((XY)\) a la línea ideal.
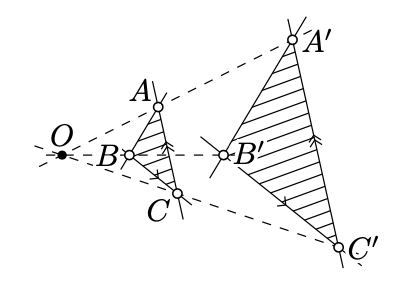
Es decir, podemos suponer que
\((BC) \parallel (B'C')\ \ \ \ \text{and} \ \ \ \ (CA) \parallel (C'A')\)
y tenemos que demostrar que
\((AB) \parallel(A'B').\)
Supongamos que las líneas\((AA')\),\((BB')\), y se\((CC')\) cruzan en el punto\(O\). Ya que\((BC) \parallel (B'C')\), la propiedad transversal (Teorema 7.3.1) implica que\(\measuredangle OBC = \measuredangle OB'C'\) y\(\measuredangle OCB = \measuredangle OC'B'\). Por la condición de similitud AA,\(\triangle OBC\z\sim\triangle OB'C'\). En particular,
\(\dfrac{OB}{OB'}=\dfrac{OC}{OC'}.\)
De la misma manera que conseguimos eso\(\triangle OAC \sim\triangle OA'C'\) y
Por lo tanto,
Por la condición de similitud SAS, obtenemos eso\(\triangle OAB\sim\triangle OA'B'\); en particular,\(\measuredangle OAB = \pm\measuredangle OA'B'\).
Tenga en cuenta que\(\measuredangle AOB=\measuredangle A'OB'\). Por lo tanto,
Por la propiedad transversal (Teorema 7.3.1), tenemos\((AB)\parallel (A'B')\).
El caso\((AA') \parallel (BB') \parallel (CC')\) se hace de manera similar. En este caso los cuadrangulares\(B'BCC'\) y\(A'ACC'\) son paralelogramos. Por lo tanto,
\(BB'=CC'=AA'.\)
De ahí\(\square B'BAA'\) es un paralelogramo y\((AB)\parallel (A'B')\).
Aquí hay otro teorema clásico de la geometría proyectiva.
Supongamos que dos triples de puntos\(A\),\(B\),\(C\), y\(A'\),\(B'\),\(C'\) son colineales. Supongamos que los puntos\(X\),\(Y\),\(Z\) están definidos de manera única por
\(X = (BC') \cap (B'C)\),\(Y = (CA') \cap (C'A)\),\(Z = (AB') \cap (A'B).\)
Entonces los puntos\(X\),\(Y\),\(Z\) son colineales.
El teorema de Pappus se puede probar de la misma manera que el teorema de Desargues.
- Idea de la Prueba
-
Aplicando una proyección de perspectiva, podemos asumir eso\(Y\) y\(Z\) tumbarnos en la línea ideal. Queda por mostrar que\(X\) se encuentra en la línea ideal.
En otras palabras, asumiendo eso\((AB') \parallel (A'B)\) y\((AC') \parallel (A'C)\), necesitamos demostrarlo\((BC') \parallel(B'C)\).
Terminar la prueba del teorema de Pappus usando la idea descrita anteriormente.
- Pista
-
Supongamos que\((AB)\) se reúne\((A'B')\) en\(O\). Ya que\((AB') \parallel (BA')\), obtenemos eso\(\triangle OAB' \sim \triangle OBA'\) y\(\dfrac{OA}{OB} = \dfrac{OB'}{OA'}\).
De igual manera\((AC') \parallel (CA')\), ya que, lo conseguimos\(\dfrac{OA}{OC} = \dfrac{OC'}{OA'}\).
Por lo tanto\(\dfrac{OB}{OC} = \dfrac{OC'}{OB'}\). Aplicando la condición de similitud SAS, lo conseguimos\(\triangle OBC' \sim \triangle OCB'\). Por lo tanto,\((BC') \parallel (CB')\).
El caso\((AB) \parallel (A'B')\) es similar.
El siguiente ejercicio da una conversa parcial al teorema de Pappus.
Dados dos triples de puntos\(A\),,\(B\), y\(C\),\(A'\),,\(B'\)\(C'\), supongamos puntos distintos\(X\),\(Y\),\(Z\) están definidos de manera única por
\(\begin{aligned} X&=(BC')\cap(B'C), & Y&=(CA')\cap(C'A), & Z&=(AB')\cap(A'B).\end{aligned}\)
Supongamos que las triples\(A\)\(B\),,\(C\), y\(X\),\(Y\),\(Z\) son colineales. Demostrar que el triple\(A'\),\(B'\),\(C'\) es colineal.
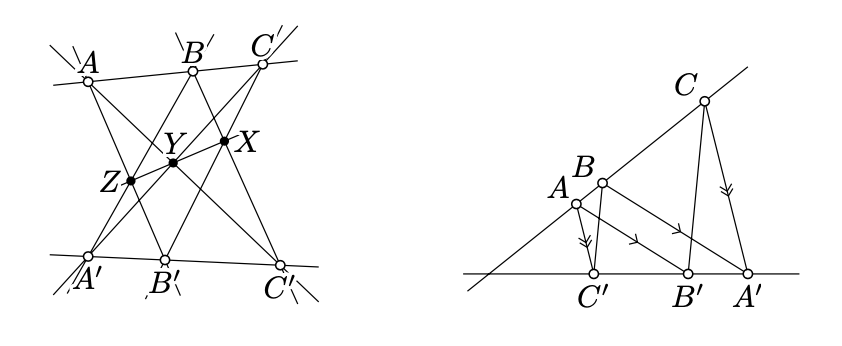
- Pista
-
Observe que la afirmación es equivalente al teorema de Pappus'.
Resolver el siguiente problema de construcción
- utilizando el teorema de Desargues;
- usando el teorema de Pappus.
- Pista
-
Para hacer (a), supongamos que el paralelogramo está formado por los dos pares de líneas paralelas\((AB) \parallel (A'B')\) y\((BC) \parallel (B'C')\) y\(\ell = (AC)\) en la notación del teorema de Desargues (Teorema\(\PageIndex{1}\))
Para hacer (b), supongamos que el paralelogramo está formado por los dos pares de paralelogramo está formado por los dos pares de líneas paralelas\((AB') \parallel (A'B')\) y\((BC') \parallel (B'C)\) y\(\ell = (AC')\) en la notación del teorema de Pappus' (Teorema\(\PageIndex{2}\)).
Supongamos que se dan un paralelogramo y una línea\(\ell\). Supongamos que la línea\(\ell\) cruza todos los lados (o sus extensiones) del paralelogramo en diferentes puntos se dan. Construye otra línea paralela a\(\ell\) con una regla solamente.


