16.2: Teorema de Pitágoras

Última actualización
Guardar como PDF

Page ID: 114389

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Aquí hay un análogo de los teoremas de Pitágoras (Teorema 6.2.1 y Teorema 13.. 1) en geometría esférica.

Teorema$\PageIndex{1}$ Spherical Pythagorean Theorem

Dejar$\triangle_sABC$ ser un triángulo esférico con un ángulo recto en$C$. Establecer$a=BC_s$,$b=CA_s$, y$c=AB_s$. Entonces

$\cos c=\cos a \cdot \cos b.$

Prueba

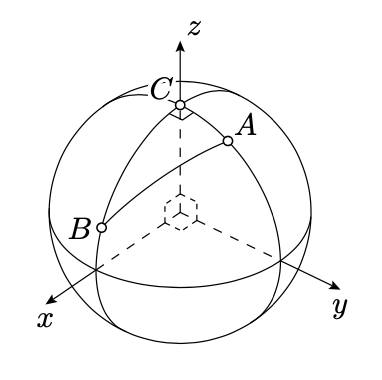
Como el ángulo a$C$ es correcto, podemos elegir las coordenadas en$\mathbb{R}^3$ para que$v_C\z=(0,0,1)$,$v_A$ yace en el$xz$ -plano, así$v_A=(x_A,0,z_A)$, y$v_B$ yace en$yz$ -plano, entonces $v_B=(0,y_B,z_B)$.

Aplicando, 16.2.3, obtenemos eso

$\begin{aligned} z_A&=\langle v_C,v_A\rangle =\cos b, \\ z_B&=\langle v_C,v_B\rangle =\cos a.\end{aligned}$

$2021-02-26 11.19.37.png$

Aplicando, 16.2.1 y 16.2.3, obtenemos que

$\begin{aligned} \cos c &=\langle v_A,v_B\rangle= \\ &=x_A\cdot 0+0\cdot y_B+z_A\cdot z_B= \\ &=\cos b\cdot\cos a.\end{aligned}$

En la prueba, usaremos la noción del producto escalar que estamos a punto de discutir.

Dejar$v_A=(x_A,y_A,z_A)$ y$v_B=(x_B,y_B,z_B)$ denotar los vectores de posición de puntos$A$ y$B$. El producto escalar de los dos vectores$v_A$ e$v_B$ in$\mathbb{R}^3$ se define como

\[\langle v_A,v_B\rangle := x_A\cdot x_B+y_A\cdot y_B+z_A\cdot z_B.\]

Supongamos que ambos vectores$v_A$ y$v_B$ son distintos de cero; supongamos que$\phi$ denota la medida del ángulo entre ellos. Entonces el producto escalar se puede expresar de la siguiente manera:

\[\langle v_A,v_B\rangle=|v_A|\cdot|v_B|\cdot\cos\phi, \]

donde

$\begin{aligned} |v_A|&=\sqrt{x_A^2+y_A^2+z_A^2}, & |v_B|&=\sqrt{x_B^2+y_B^2+z_B^2}.\end{aligned}$

Ahora bien, supongamos que los puntos$A$ y$B$ se encuentran en la esfera unitaria$\Sigma$ en$\mathbb{R}^3$ centrado en el origen. En este caso$|v_A|=|v_B|=1$. Por 16.2.2 obtenemos eso

\[\cos AB_s=\langle v_A,v_B\rangle.\]

Ejercicio$\PageIndex{1}$

comoCómo que si$\triangle_s ABC$ es un triángulo esférico con un ángulo recto en$C$, y$AC_s=BC_s=\dfrac{\pi}{4}$, entonces$AB_s=\dfrac{\pi}{3}$.

Pista

$2021-02-26 11.24.50.png$

Aplicando el teorema de Pitágoras, obtenemos que

$\cos AB_s = \cos AC_s \cdot \cos BC_s = \dfrac{1}{2}.$

Por lo tanto,$AB_s = \dfrac{\pi}{3}.$

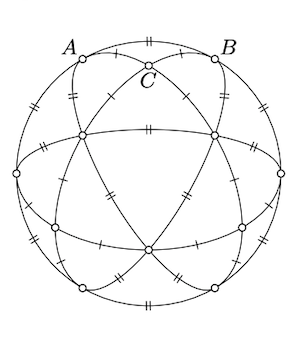
Alternativamente, mire la teselación de un hemisferio en la imagen; está hecha de 12 copias$\triangle_s ABC$ y sin embargo de 4 triángulos esféricos equiláteros. De la simetría de esta teselación, se deduce que$[AB]_s$ ocupa$\dfrac{1}{6}$ del ecuador; es decir,$AB_s = \dfrac{\pi}{3}$.