16.3: Inversión del espacio

Última actualización
Guardar como PDF

Page ID: 114393

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

La inversión en una esfera se define de la misma manera que definimos la inversión en un círculo.

Formalmente, deja$\Sigma$ ser la esfera con el centro$O$ y el radio$r$. La inversión en$\Sigma$ de un punto$P$ es el punto$P'\in[OP)$ tal que

$OP\cdot OP'=r^2.$

En este caso, la esfera se$\Sigma$ llamará esfera de inversión y su centro se llamará centro de inversión.

También agregamos$\infty$ al espacio y asumimos que el centro de inversión está mapeado$\infty$ y al revés. El espacio$\mathbb{R}^3$ con el punto$\infty$ se llamará espacio inversivo.

La inversión del espacio tiene muchas propiedades de la inversión del plano. Lo más importante para nosotros son los análogos del Teorema 10.2.1, Teorema 10.3.1 y Teorema 10.6.1 los cuales pueden resumirse de la siguiente manera:

Teorema$\PageIndex{1}$

La inversión en la esfera tiene las siguientes propiedades:

La inversión mapea una esfera o un plano en una esfera o un plano.
La inversión mapea un círculo o una línea en un círculo o una línea.
La inversión conserva la relación cruzada; es decir, si$A'$,$B'$,$C'$, y$D'$ son las inversas de los puntos$A$$B$,$C$ y$D$ respectivamente, entonces \[\dfrac{AB\cdot CD}{BC\cdot DA}= \dfrac{A'B'\cdot C'D'}{B'C'\cdot D'A'}.\]
La inversión mapea los arcos en arcos.
La inversión conserva el valor absoluto de la medida del ángulo entre medias líneas tangentes a los arcos.

Aquí no presentamos las pruebas, pero casi repiten las pruebas correspondientes en geometría plana. Para acreditar (a), necesitará además el siguiente lema; su prueba se deja al lector.

Lema$\PageIndex{1}$

Dejar$\Sigma$ ser un subconjunto del espacio euclidiano que contenga al menos dos puntos. Fijar un punto$O$ en el espacio.

Entonces$\Sigma$ es una esfera si y solo si para cualquier plano$\Pi$ que pasa a través$O$, la intersección$\Pi \cap \Sigma$ es un conjunto vacío, un conjunto de puntos o un círculo.

La siguiente observación ayuda a reducir la parte (b) a la parte (a).

Observación$\PageIndex{1}$

Cualquier círculo en el espacio es una intersección de dos esferas.

Definamos un cono circular como un conjunto formado por segmentos de línea desde un punto fijo, llamado punta del cono, hasta todos los puntos de un círculo fijo, llamado base del cono; siempre suponemos que la base no se encuentra en el mismo plano que la punta. Decimos que el cono tiene razón si el centro del círculo base es el punto del pie de la punta en el plano base; de lo contrario lo llamamos oblicuo.

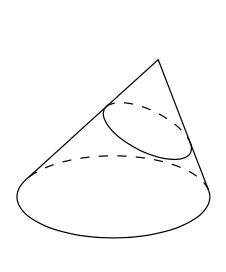
$2021-03-01 10.14.22.png$

Ejercicio$\PageIndex{1}$

Dejar$K$ ser un cono circular oblicuo. Mostrar que hay un plano$\Pi$ que no es paralelo al plano base de$K$ tal manera que la intersección$\Pi\cap K$ es un círculo.

Sugerencia: Considera la inversión de la base en una esfera con el centro en la punta del cono y aplica el Teorema$\PageIndex{1}$.

Teorema\(\PageIndex{1}\)

Lema\(\PageIndex{1}\)

Observación\(\PageIndex{1}\)

Ejercicio\(\PageIndex{1}\)