16.4: Proyección estereográfica
- Page ID
- 114386
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)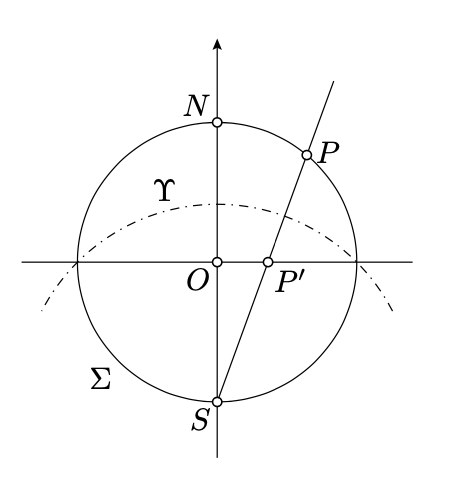
Considera la esfera unitaria\(\Sigma\) centrada en el origen\((0,0,0)\). Esta esfera puede ser descrita por la ecuación\(x^2+y^2+z^2=1\).
Supongamos que\(\Pi\) denota el\(xy\) -plano; se define por la ecuación\(z = 0\). Claramente,\(\Pi\) corre por el centro de\(\Sigma\).
Dejar\(N = (0, 0, 1)\) y\(S=(0, 0, -1)\) denotar los polos “norte” y “sur” de\(\Sigma\); estos son los puntos en la esfera que tienen distancias extremas a\(\Pi\). Supongamos que\(\Omega\) denota el “ecuador” de\(\Sigma\); es la intersección\(\Sigma \cap \Pi\).
Para cualquier punto\(P\ne S\)\(\Sigma\), considere la línea\((SP)\) en el espacio. Esta línea se cruza exactamente\(\Pi\) en un punto, denotado por\(P'\). Set\(S'=\infty\).
Al mapa\(\xi_s\: P\mapsto P'\) se le llama la proyección estereográfica de\(\Sigma\) a \(\Pi\)con respecto al polo sur. A la inversa de este mapa\(\xi^{-1}_s\: P' \mapsto P\) se le llama la proyección estereográfica de\(\Pi\) a \(\Sigma\)con respecto al polo sur.
De la misma manera, se pueden definir las proyecciones estereográficas\(\xi_n\) y\(\xi^{-1}_n\) con respecto al polo norte\(N\).
Tenga en cuenta que\(P=P'\) si y solo si\(P\in\Omega\).
Obsérvese que si\(\Sigma\) y\(\Pi\) son como arriba, entonces la composición de las proyecciones estereográficas\(\xi_s: \Sigma\to\Pi\) y\(\xi^{-1}_s: \Pi\to\Sigma\) son las restricciones a\(\Sigma\) y\(\Pi\) respectivamente de la inversión en la esfera \(\Upsilon\)con el centro\(S\) y el radio\(\sqrt{2}\).
Desde arriba y Teorema 16.3.1, se deduce que la proyección estereográfica preserva los ángulos entre arcos; más precisamente el valor absoluto de la medida angular entre arcos sobre la esfera.
Esto lo hace particularmente útil en cartografía. Un mapa de una gran región de la tierra no se puede hacer a una escala constante, pero usando una proyección estereográfica, se pueden mantener los ángulos entre las carreteras de la misma manera que en la tierra.
En los siguientes ejercicios, asumimos que\(\Sigma\),\(\Pi\),\(\Upsilon\),\(\Omega\),\(O\),\(S\), y\(N\) son los anteriores.
Demostrar que\(\xi_n \circ \xi^{-1}_s\), la composición de las proyecciones estereográficas\(\Sigma\) de\(\Pi\) a desde\(S\), y\(\Pi\) de\(\Sigma\) a desde\(N\) es la inversa del plano\(\Pi\) pulg\(\Omega\).
- Pista
-
Tenga en cuenta que los puntos en\(\Omega\) no se mueven. Además, los puntos del interior\(\Omega\) se mapean fuera\(\Omega\) y al revés.
Además, tenga en cuenta que este mapa envía círculos a círculos; además, los círculos perpendiculares se mapean a círculos perpendiculares. En particular, los círculos perpendiculares a\(\Omega\) se mapean a sí mismos.
Considerar punto arbitrario\(P \not\in \Omega\). Supongamos que\(P'\) denota la inversa de\(P\) in\(\Omega\). Elija dos círculos distintos que pasen a través\(P\) y\(P'\). De acuerdo con Corolario 10.5.2,\(\Gamma_1 \perp \Omega\) y\(\Gamma_2 \perp \Omega\).
Por lo tanto, lo inverso en\(\Omega\) envía\(\Gamma_1\) a sí mismo y lo mismo sostiene para\(\Gamma_2\).
La imagen de\(P\) tiene que mentir sobre\(\Gamma_1\) y\(\Gamma_2\). Como la imagen de\(P\) es distinta de\(P\), obtenemos que tiene que ser\(P'\).
Mostrar que una proyección estereográfica\(\Sigma\to\Pi\) envía los grandes círculos a círculos planos que se cruzan\(\Omega\) en puntos opuestos.
- Pista
-
Aplicar Teorema 16.3.1 (b).
El siguiente ejercicio es análogo al Lema 13.5.1.
Fijar un punto\(P\in \Pi\) y dejar\(Q\) ser otro punto adentro\(\Pi\). Dejar\(P'\) y\(Q'\) denotar sus proyecciones estereográficas a\(\Sigma\). Establecer\(x=PQ\) y\(y=P'Q'_s\). Demostrar que
\(\lim_{x\to 0} \dfrac{y}{x}=\dfrac{2}{1+OP^2}.\)
- Pista
-
Set\(z = P'Q'\). Tenga en cuenta que\(\dfrac{y}{x} \to 1\) como\(x \to 0\).
Queda por shwo que
\(\lim_{x \to 0} \dfrac{z}{x} = \dfrac{2}{OP^2}\)
Recordemos que la proyección estereográfica es la inversión en la esfera\(Upsilon\) con el centro en el polo sur\(S\) restringido al plano\(\Pi\). Demostrar que hay un avión\(\Lambda\) pasando por\(S, P, Q, P'\), y\(Q'\). En el plano\(\Lambda\), el mapa\(Q \mapsto Q'\) es una inversión en el círculo\(\Upsilon \cap \Lambda\).
Esto reduce el problema a la geometría del plano euclidiano. Los cálculos restantes en\(\Lambda\) son similares a los de la prueba de Lemma 13.5.1.


