17.1: Biyección especial en el plano h
- Page ID
- 114439
Considere el modelo de disco conforme con el absoluto en el círculo unitario\(\Omega\) centrado en\(O\). Elija un sistema de coordenadas\((x,y)\) en el plano con el origen en\(O\), para que el círculo\(\Omega\) se describa mediante la ecuación\(x^2+y^2=1\).
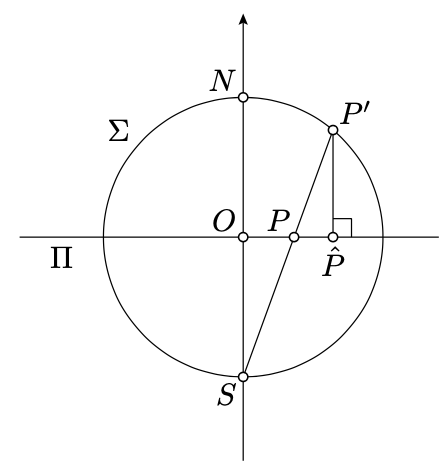
El avión a través\(P, O\), y\(S\).
Pensemos que nuestro plano es el\(xy\) plano coordenado en el espacio euclidiano; denotarlo por\(\Pi\). \(\Sigma\)Sea la esfera unitaria centrada en\(O\); se describe por la ecuación
\(x^2+y^2+z^2=1.\)
Conjunto\(S=(0,0,-1)\) y\(N=(0,0,1)\); estos son los polos sur y norte de\(\Sigma\).
Considerar proyección estereográfica\(\Pi\to\Sigma\) desde\(S\); punto dado\(P\in\Pi\) denotar su imagen en\(\Sigma\). Obsérvese que el plano h está mapeado al hemisferio norte; es decir, al conjunto de puntos\((x,y,z)\) en\(\Sigma\) descrito por la desigualdad\(z>0\).
Por un punto\(P'\in \Sigma\) considera su punto de\(\hat P\) pie\(\Pi\); este es el punto más cercano al\(P'\).
Tenga en cuenta que la composición\(P \leftrightarrow P' \leftrightarrow \hat{P}\) de estos dos mapas da una bijección desde el plano h a sí mismo. Además, tenga en cuenta que\(P=\hat{P}\) si y sólo si\(P\in \Omega\) o\(P=O\).
Supongamos que\(P\leftrightarrow \hat P\) es la bijección descrita anteriormente. Supongamos que\(P\) es un punto de plano h distinto del centro de absoluto y\(Q\) es su inverso en el absoluto. Demostrar que el punto medio de\([PQ]\) es la inversión de\(\hat{P}\) en lo absoluto.
- Sugerencia
-
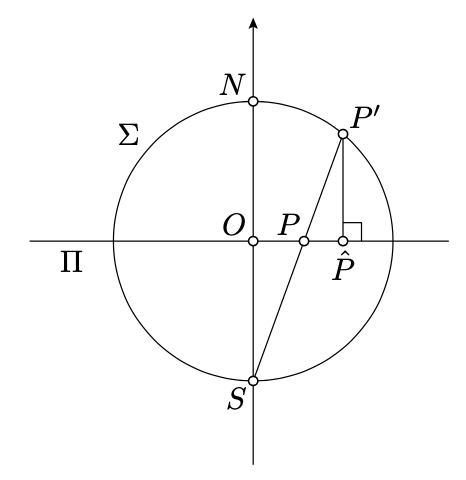
Dejar\(N, O, S, P, P'\) y\(\hat{P}\) ser como en el diagrama anterior.
Obsérvese eso\(QQ = \dfrac{1}{x}\) y por lo tanto tenemos que demostrarlo\(O\hat{P} = 2/(x + \dfrac{1}{x})\). Para ello, muestra y usa eso\(\triangle SOP \sim \triangle SP'N \sim \triangle P'\hat{P}P\) y\(2 \cdot SO = NS\).
Dejar\((PQ)_h\) ser una línea h con los puntos ideales\(A\) y\(B\). Entonces\(\hat P,\hat Q\in[AB]\).
Además,
\[\dfrac{A \hat{Q} \cdot B \hat{P}}{\hat{QB}\cdot \hat{P}A} = (\dfrac{AQ\cdot BP}{QB\cdot PA})^2. \]
En particular, si\(A,P,Q,B\) aparecen en el mismo orden, entonces
\(PQ_h=\dfrac{1}{2} \cdot \ln \dfrac{A\hat{Q}\cdot B\hat{P}}{\hat{Q}B\cdot \hat{P}A}.\)
- Prueba
-
Considerar la proyección estereográfica\(\Pi \to \Sigma\) desde el polo sur\(S\). Tenga en cuenta que fija\(A\) y\(B\); denota por\(P'\) y\(Q'\) las imágenes de\(P\) y\(Q\);
Según el Teorema 16.3.1c,
\[\dfrac{AQ\cdot BP}{QB\cdot PA}=\dfrac{AQ'\cdot BP'}{Q'B\cdot P'A}.\]
Por Teorema Teorema 16.3.1e, cada circlina en\(\Pi\) que es perpendicular a\(\Omega\) se mapean a un círculo en el\(\Sigma\) que sigue siendo perpendicular a\(\Omega\). De ello se deduce que la proyección estereográfica envía\((PQ)_h\) a la intersección del hemisferio norte de\(\Sigma\) con un plano perpendicular a\(\Pi\).
Supongamos que\(\Lambda\) denota el plano; contiene los puntos\(A\)\(B\),\(P'\),,\(\hat P\) y el círculo\(\Gamma=\Sigma\cap\Lambda\). (También contiene\(Q'\) y\(\hat{Q}\) pero no vamos a utilizar estos puntos por un tiempo.)
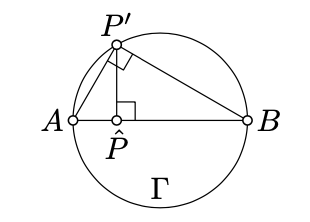
El avión\(\Lambda\).Tenga en cuenta que
- \(A,B,P'\in\Gamma\),
- \([AB]\)es un diámetro de\(\Gamma\),
- \((AB)=\Pi\cap\Lambda\),
- \(\hat{P} \in [AB]\)
- \((P'\hat{P} \perp (AB).\)
Dado que\([AB]\) es el diámetro de\(\Gamma\), por Corolario 9.8, el ángulo\(AP'B\) es recto. De ahí\(\triangle A\hat PP' \sim \triangle AP'B \sim \triangle P'\hat PB\). En particular
\(\dfrac{AP'}{BP'}=\dfrac{A \hat{P}}{P'\hat{P}}=\dfrac{P'\hat{P}}{B\hat{P}}.\)
Por lo tanto
\[\dfrac{A\hat{P}}{B\hat{P}}=(\dfrac{AP'}{BP'})^2.\]
De la misma manera que lo conseguimos
\[\dfrac{A\hat{Q}}{B\hat{Q}}=(\dfrac{AQ'}{BQ'})^2.\]
Por último, señalar que 17.1.2+17.1.3+17.1.4 implican 17.1.1
El último enunciado se desprende de 17.1.1 y la definición de h-distancia. En efecto,
\(\begin{aligned} PQ_h&:=\ln\frac{A Q\cdot B P}{QB\cdot PA}= \\ &=\ln\left(\frac{A \hat Q\cdot B \hat P}{\hat QB\cdot \hat PA}\right)^{\frac12}= \\ &=\tfrac12\cdot\ln\frac{A \hat Q\cdot B \hat P}{\hat QB\cdot \hat PA}.\end{aligned}\)
Dejar\(\Gamma_1\),\(\Gamma_2\), y\(\Gamma_3\) ser tres círculos perpendiculares al círculo\(\Omega\). Dejar\([A_1B_1]\),\([A_2B_2]\), y\([A_3B_3]\) denotar los acordes comunes de\(\Omega\) y\(\Gamma_1\),\(\Gamma_2\),\(\Gamma_3\) respectivamente. Mostrar que los acordes\([A_1B_1]\),\([A_2B_2]\), y se\([A_3B_3]\) cruzan en un punto dentro\(\Omega\) si y sólo si\(\Gamma_1\)\(\Gamma_2\), y se\(\Gamma_3\) cruzan en dos puntos.
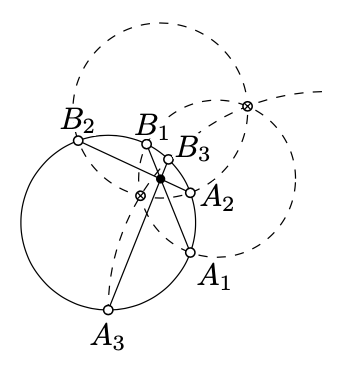
- Sugerencia
-
Considera la biyección\(P \leftrightarrow \hat{P}\) del plano h con absoluto\(\Omega\). Tenga en cuenta que\(\hat{P} \in [A_iB_i]\) si y solo si\(P \in \Gamma_i\).


