18.4: Fórmula de Euler

Última actualización
Guardar como PDF

Page ID: 114730

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\alpha$Déjese ser un número real. La siguiente identidad se llama fórmula de Euler:

\[e^{i\cdot\alpha}=\cos\alpha+i\cdot\sin\alpha.\]

En particular,$e^{i\cdot\pi}=-1$ y$e^{i\cdot\frac\pi2}=i$.

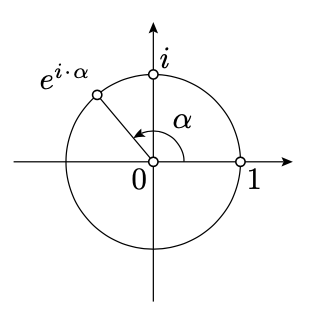
$2021-03-01 2.31.24.png$

Geométricamente, la fórmula de Euler significa lo siguiente: Supongamos que$O$ y$E$ son los puntos con coordenadas complejas$0$ y$1$ respectivamente. Asumir

$OZ=1\quad \text{and}\quad \measuredangle EOZ \equiv \alpha,$

entonces$e^{i\cdot\alpha}$ es la compleja coordenada de$Z$. En particular, la coordenada compleja de cualquier punto del círculo unitario centrado en$O$ puede expresarse de manera única como$e^{i\cdot\alpha}$ para algunos$\alpha\in(-\pi,\pi]$.

¿Por qué debería pensar que 18.4.1 es cierto?

La prueba de la identidad de Euler depende de la forma en que defina la función exponencial. Si nunca tuviste que aplicar la función exponencial a un número imaginario, puedes tomar el lado derecho en 18.4.1 como definición del$e^{i\cdot\alpha}$.

En este caso, formalmente no hay que probar nada, pero es mejor verificar que$e^{i\cdot\alpha}$ satisfaga identidades familiares. Principalmente,

$e^{i\cdot \alpha}\cdot e^{i\cdot \beta}= e^{i\cdot(\alpha+\beta)}.$

Esto último se puede probar usando 18.1.2 y las siguientes fórmulas trigonométricas, que suponemos que se conocen:

$\begin{aligned} \cos(\alpha+\beta)&=\cos\alpha\cdot\cos\beta-\sin\alpha\cdot\sin\beta, \\ \sin(\alpha+\beta)&=\sin\alpha\cdot\cos\beta+\cos\alpha\cdot\sin\beta.\end{aligned}$

Si conoces la serie de potencias para la función sinusoidal, coseno y exponencial, entonces lo siguiente podría convencer de que la identidad 18.4.1 se mantiene:

$\begin{aligned} e^{i\cdot \alpha } &{}= 1 + i\cdot \alpha + \frac{(i\cdot \alpha )^2}{2!} + \frac{(i\cdot \alpha )^3}{3!} + \frac{(i\cdot \alpha )^4}{4!} + \frac{(i\cdot \alpha )^5}{5!} + \cdots = \\ &= 1 + i\cdot \alpha - \frac{\alpha ^2}{2!} - i\cdot\frac{ \alpha ^3}{3!} + \frac{\alpha ^4}{4!} + i\cdot\frac{ \alpha ^5}{5!} - \cdots = \\ &= \left( 1 - \frac{\alpha ^2}{2!} + \frac{\alpha ^4}{4!} - \cdots \right) + i\cdot\left( \alpha - \frac{\alpha ^3}{3!} + \frac{\alpha ^5}{5!} - \cdots \right) = \\ &= \cos \alpha + i\cdot\sin \alpha.\end{aligned}$