18.5: Argumento y coordenadas polares

Última actualización
Guardar como PDF

Page ID: 114782

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Como antes, asumimos que$O$ y$E$ son los puntos con coordenadas complejas$0$ y$1$ respectivamente.

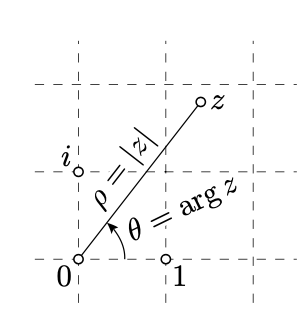
Dejar$Z$ ser un punto de forma distinta$O$. Establecer$\rho=OZ$ y$\theta=\measuredangle EOZ$. El par$(\rho,\theta)$ se llama las coordenadas polares de$Z$.

Si$z$ es la compleja coordenada de$Z$, entonces$\rho=|z|$. Al valor$\theta$ se le llama el argumento de$z$ (brevemente,$\theta=\arg z$). En este caso,

$z=\rho\cdot e^{i\cdot\theta}=\rho\cdot(\cos\theta+i\cdot\sin\theta).$

$2021-03-01 2.35.41.png$

Tenga en cuenta que

$\arg (z\cdot w) \equiv \arg z+\arg w$

$\arg \tfrac z w \equiv \arg z-\arg w$

si$z \ne 0$ y$w \ne 0$. En particular, si$Z$$V$,$W$ son puntos con coordenadas complejas$z$$v$, y$w$ respectivamente, entonces

\[\begin{aligned} \measuredangle VZW &=\arg\left(\frac{w-z}{v-z}\right)\equiv \\ &\equiv \arg(w-z)-\arg(v-z) \end{aligned}\]

si$\measuredangle VZW$ se define.

Ejercicio$\PageIndex{1}$

Usa la fórmula 18.5.1 para demostrar que

$\measuredangle ZVW+\measuredangle VWZ+\measuredangle WZV\equiv \pi$

para cualquiera$\triangle ZVW$ en el plano euclidiano.

Insinuación

Dejar$z, v$, y$w$ denotar las coordenadas complejas de$Z, V$, y$W$ respectivamente. Entonces

$\begin{array} {rcl} {\measuredangle ZVW + \measuredangle VWZ + \measuredangle WZV} & \equiv & {\arg \dfrac{w - v}{z- v} + \arg \dfrac{z-w}{v-w} + \arg \dfrac{v-z}{w-z} \equiv} \\ {} & \equiv & {\arg \dfrac{(w - v) \cdot (z - w) \cdot (v -z)}{(z - v) \cdot (v - w) \cdot (w - z)} \equiv} \\ {} & \equiv & {\arg (-1) \equiv \pi} \end{array}$

Ejercicio$\PageIndex{2}$

Supongamos que los puntos$O$$E$$V$,$W$,,, y$Z$ tienen coordenadas complejas$0$$1$,,$v$,$w$, y$z=v\cdot w$ respectivamente. Demostrar que

$\triangle OEV\sim \triangle OWZ.$

Insinuación: Tenga en cuenta y use eso$\measuredangle EOV = \measuredangle WOZ = \arg v$ y$\dfrac{OW}{OZ} = \dfrac{OZ}{OW} = |v|$.

El siguiente teorema es una reformulación del Corolario 9.3.2 que utiliza coordenadas complejas.

Teorema$\PageIndex{1}$

Dejar$\square UVWZ$ ser un cuadriángulo y$u$$v$,$w$,, y$z$ ser las complejas coordenadas de sus vértices. Entonces$\square UVWZ$ se inscribe si y sólo si el número

$\dfrac{(v-u)\cdot(z-w)}{(v-w)\cdot(z-u)}$

es real.

El valor$\dfrac{(v-u)\cdot(w-z)}{(v-w)\cdot(z-u)}$ se denomina relación cruzada compleja de$u$,$w$,$v$, y$z$; se denotará por$(u,w;v,z)$.

Ejercicio$\PageIndex{1}$

Observe que el número complejo$z\ne 0$ es real si y sólo si$\arg z=0$ o$\pi$; en otras palabras,$2\cdot\arg z\equiv 0$.

Utilice esta observación para demostrar que el Teorema$\PageIndex{1}$ es efectivamente una reformulación del Corolario 9.3.2.

Insinuación

Tenga en cuenta que

$\arg \dfrac{(v-u) \cdot (z-w)}{(v -w) \cdot (z -u)} \equiv \arg \dfrac{v - u}{z - u} + \arg \dfrac{z- w}{v -w} = \measuredangle ZUV + \measuredangle VWZ.$

La declaración sigue ya que el valor$\dfrac{(v - u) \cdot (x - w)}{(v - w) \cdot (z - u)}$ es real si y solo si

$2 \cdot \arg \dfrac{(v - u) \cdot (z - w)}{(v - w) \cdot (z - u)} \equiv 0.$

Ejercicio\(\PageIndex{1}\)

Ejercicio\(\PageIndex{2}\)

Teorema\(\PageIndex{1}\)

Ejercicio\(\PageIndex{1}\)