19.3: Construcciones con un conjunto cuadrado

Última actualización
Guardar como PDF

Page ID: 114642

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

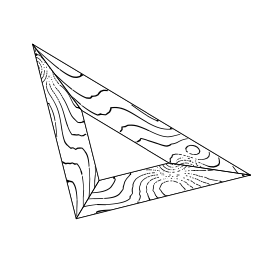
$2021-03-02 10.14.12.png$

Un conjunto cuadrado es una herramienta de construcción que se muestra en la imagen; puede producir una línea a través de un punto dado que forma los ángulos$\tfrac\pi2$ o$\pm\tfrac\pi4$ a una línea dada y también se puede usar como regla; es decir, puede producir una línea a través de un par de puntos dado.

Ejercicio$\PageIndex{1}$

Trisectar un segmento dado con un conjunto cuadrado.

Pista: Tenga en cuenta que con un conjunto cuadrado podemos construir una línea paralela a una línea dada a través del punto dado. Queda por modificar la construcción en el Ejercicio 14.2.1.

Consideremos las construcciones set-square. Siguiendo las mismas líneas que en la sección anterior, podemos definir los números constructibles de set-square y probar el siguiente análogo del Teorema 19.2.1:

Teorema$\PageIndex{1}$

Teorema Supongamos que la configuración inicial de una construcción geométrica viene dada por los puntos$A_1=(0,0)$,$A_2=(1,0)$,$A_3=(x_3,y_3),\dots,A_n=(x_n,y_n)$. Entonces se$X=(x,y)$ puede construir un punto usando una construcción de conjunto cuadrado si y solo si ambas coordenadas$x$ y se$y$ pueden expresar a partir de los números enteros y$x_3$,$y_3$,$x_4$, $y_4,\dots,x_n$,$y_n$ utilizando$/$" únicamente las operaciones aritméticas "$+$"$-$","$\cdot$", "y".

Apliquemos este teorema para mostrar la imposibilidad de algunas construcciones con un conjunto cuadrado.

Tenga en cuenta que si todas las coordenadas$x_3,y_3,\dots,x_n,y_n$ son números racionales, entonces el teorema anterior implica que con un conjunto cuadrado, solo se pueden construir los puntos con coordenadas racionales. Un punto con ambas coordenadas racionales se llama racional, y si al menos una de las coordenadas es irracional, entonces el punto se llama irracional.

Ejercicio$\PageIndex{2}$

Mostrar que un triángulo equilátero en el plano euclidiano tiene al menos un punto irracional.

Concluimos que con un conjunto cuadrado, no se puede construir un triángulo equilátero con una base dada.

Pista: Supongamos que dos vértices tienen coordenadas racionales, digamos$(a_1, b_1)$ y$(a_2, b_2)$. Encuentra las coordenadas del tercer vértice. Usa que el número$\sqrt{3}$ es irracional para mostrar que el tercer vértice es un punto irracional.

Ejercicio\(\PageIndex{1}\)

Teorema\(\PageIndex{1}\)

Ejercicio\(\PageIndex{2}\)