19.2: Números construtibles
- Page ID
- 114631
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)En las construcciones clásicas de brújula y regla, la configuración inicial puede describirse completamente por un número finito de puntos; cada línea está definida por dos puntos en ella y cada círculo se describe por su centro y un punto sobre él (equivalentemente, se puede describir un círculo por tres puntos sobre él).
De la misma manera se puede describir el resultado de la construcción mediante una colección finita de puntos.
Siempre podemos suponer que la configuración inicial tiene al menos dos puntos; si no sumamos uno o dos puntos a la configuración. Además, aplicando una escala a todo el plano, podemos suponer que los dos primeros puntos en la configuración inicial se encuentran a una distancia 1 uno del otro.
En este caso podemos elegir un sistema de coordenadas, tal que uno de los puntos iniciales sea el origen\((0,0)\) y otro punto inicial tenga las coordenadas\((1,0)\). En este sistema de coordenadas, la configuración inicial de\(n\) los puntos se describe por\(2\cdot n-4\) números, sus coordenadas\(x_3,y_3,\dots,x_n,y_n\).
Resulta que las coordenadas de cualquier punto construido con brújula y regla se pueden escribir a través de los números\(x_3,y_3,\dots,x_n,y_n\) usando las cuatro operaciones aritméticas "\(+\)"\(-\)","\(\cdot\)", "\(/\)"y la raíz cuadrada” \(\sqrt{\phantom{a}}\)".
Por ejemplo, supongamos que queremos encontrar los puntos\(X_1=(x_1,y_1)\) y\(X_2=(x_2,y_2)\) de las intersecciones de una línea que pasa a través\(A=(x_A,y_A)\)\(B=(x_B,y_B)\) y y el círculo con centro\(O=(x_O,y_O)\) que pasa por el punto\(W=(x_W,y_W)\). Escribamos las ecuaciones del círculo y la línea en las coordenadas\((x,y)\):
Tenga en cuenta que las coordenadas\((x_1,y_1)\) y\((x_2,y_2)\) de los puntos\(X_1\) y\(X_2\) son soluciones de este sistema. Expresando\(y\) a partir de la segunda ecuación y sustituyendo el resultado en la primera, nos da una ecuación cuadrática en\(x\), la cual puede resolverse usando "\(+\)"\(-\)","\(\cdot\)", "\(/\)"y” \(\sqrt{\phantom{a}}\)"solamente.
Lo mismo se puede realizar para la intersección de dos círculos. La intersección de dos líneas es aún más simple; se describe como una solución de dos ecuaciones lineales y se puede expresar utilizando sólo cuatro operaciones aritméticas; la raíz cuadrada "no\(\sqrt{\phantom{a}}\)" es necesaria.
Por otro lado, es fácil hacer construcciones de brújula y regla que produzcan segmentos de las longitudes\(a+b\) y\(a-b\) a partir de dos segmentos dados de longitudes\(a>b\).
Para realizar "\(\cdot\)","\(/\)" y "\(\sqrt{\phantom{a}}\)"considerar el siguiente diagrama: dejar\([AB]\) ser un diámetro de un círculo; fijar un punto\(C\) en el círculo y dejar\(D\) ser el punto del pie de\(C\) on \([AB]\). Por Corolario 9.3.1, el ángulo\(ACB\) es recto. Por lo tanto
\(\triangle ABC\sim\triangle ACD\sim \triangle CBD.\)
De ello se deduce que\(AD\cdot BD=CD^2\).
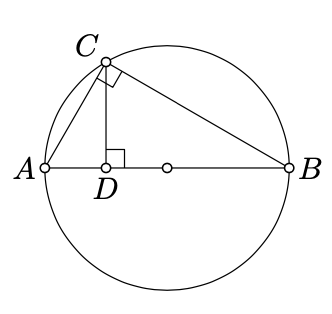
Usando este diagrama, se debe adivinar una solución al siguiente ejercicio.
Dados dos segmentos de línea con longitudes\(a\) y\(b\), dar una construcción de regla y brújula de unos segmentos con longitudes\(\tfrac {a^2}b\) y\(\sqrt{a\cdot b}\).
- Sugerencia
-
Para construir\(\sqrt{a \cdot b}\): (1) construir puntos\(A, B\), y\(D \in [AB]\) tal que\(AD = a\) y\(BD =b\); (2) construir el círculo\(\Gamma\) en el diámetro\([AB]\); (3) dibujar la línea a\(\ell\) través\(D\) perpendicular a\((AB)\); (4) dejar\(C\) ser una intersección de\(\Gamma\) y\(\ell\). Entonces\(DC = \sqrt{a \cdot b}\).
La construcción de\(\dfrac{a^2}{b}\) es análoga.
Tomando\(1\) por\(a\) o\(b\) por encima, podemos producir\(\sqrt a\),\(a^2\),\(\tfrac1b\). Combinando estas construcciones podemos producir\(a\cdot b=(\sqrt{a\cdot b})^2\),\(\tfrac ab=a\cdot\tfrac 1b\). En otras palabras, producimos una calculadora de brújula y regla que puede hacer "\(+\)"\(-\)","\(\cdot\)"\(/\)", "y"”\(\sqrt{\phantom{a}}\)".
La discusión anterior da un boceto de la prueba del siguiente teorema:
Supongamos que la configuración inicial de la construcción geométrica viene dada por los puntos\(A_1=(0,0)\),\(A_2=(1,0)\),\(A_3=(x_3,y_3),\dots,A_n=(x_n,y_n)\). Entonces se\(X=(x,y)\) puede construir un punto usando una construcción de brújula y regla si y solo si ambas coordenadas\(x\) y se\(y\) pueden expresar a partir de los números enteros y\(x_3\),\(y_3\),\(x_4\), \(y_4,\dots,x_n,y_n\)utilizando las operaciones aritméticas "\(+\)"\(-\)",", "\(\cdot\)"\(/\)"," y la raíz cuadrada”\(\sqrt{\phantom{a}}\)".
Los números que se pueden expresar a partir de los números dados usando las operaciones aritméticas y la raíz cuadrada “\(\sqrt{\phantom{a}}\)” se llaman constructibles; si no se da la lista de números dados, entonces solo podemos usar los enteros.
El teorema anterior traduce cualquier problema de construcción de brújula y regla en un lenguaje puramente algebraico. Por ejemplo:
- La imposibilidad de una solución para duplicar el problema del cubo indica que no\(\sqrt[3]{2}\) es un número construible. Eso\(\sqrt[3]{2}\) no se puede expresar a través de enteros usando "\(+\)","\(-\)"\(\cdot\)", "\(/\)"," y "\(\sqrt{\phantom{a}}\)".
- La imposibilidad de una solución para cuadrar el círculo establece que\(\sqrt{\pi}\), o equivalentemente\(\pi\), no es un número construible.
- El teorema de Gauss-Wantzel dice para qué enteros\(\cos\tfrac{2\cdot\pi}n\) es construible\(n\) el número.
Algunas de estas afirmaciones pueden parecer evidentes, pero las pruebas rigurosas requieren cierto conocimiento del álgebra abstracta (es decir, la teoría de campo) que está fuera del alcance de este libro.
En la siguiente sección, discutimos ejemplos similares pero más simples de construcciones imposibles con una herramienta inusual.
- Demuestre que el pentágono diagonal o regular es\(\tfrac{1+\sqrt5}2\) veces más grande que su lado.
- Use (a) para hacer una construcción de brújula y regla de un pentágono regular.
- Sugerencia
-
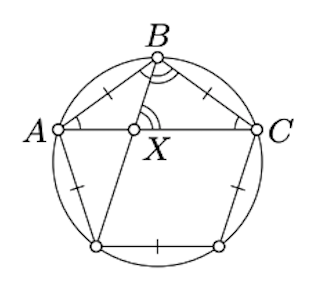
(a) Mira el diagrama del pentágono regular; mostrar que los ángulos marcados de la misma manera tienen la misma medición de ángulo. Concluir el que\(XC =BC\) y\(\triangle ABC \sim \triangle AXB\). Por lo tanto
\(\dfrac{AB}{AC} = \dfrac{AX}{AB} = \dfrac{AC - AB}{AB} = \dfrac{AC}{AB} - 1\).
Queda por resolver para\(\dfrac{AC}{AB}\).
(b) Elegir dos puntos\(P\) y\(Q\) y utilizar la calculadora de brújula y regla para construir dos puntos\(V\) y\(W\) tal que\(VW = \dfrac{1 + \sqrt{5}}{2} \cdot PQ\). Después construye un pentágono con los lados\(PQ\) y diagonales\(VW\).


