20.4: Área de fuga y subdivisiones
- Page ID
- 114498
Cualquier conjunto de un punto así como cualquier segmento en el plano euclidiano tienen área de fuga.
- Prueba
-
Fijar un segmento de línea\([AB]\). Considera un cuadrado vendido\(\blacksquare ABCD\).
Tenga en cuenta que dado un entero positivo\(n\), hay segmentos\(n\) disjuntos\([A_1B_1],\dots,[A_nB_n]\) en\(\blacksquare ABCD\), de tal manera que cada uno\([A_iB_i]\) es congruente\([AB]\) en el sentido de la Definición 20.1.1.
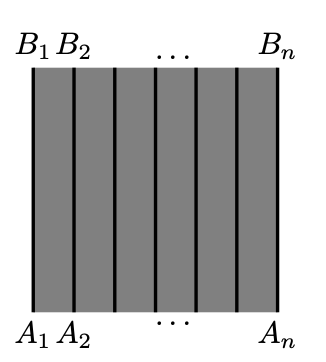
Aplicando invarianza, aditividad y monotonicidad de la función de área, obtenemos que
\(\begin{aligned} n\cdot \text{area }[AB] &=\text{area }\left([A_1B_1]\cup\dots\cup[A_nB_n]\right)\le \\ &\le \text{area }(\blacksquare ABCD) \end{aligned}\)
Es decir,
\(\text{area }[AB]\le \tfrac1n\cdot\text{area }(\blacksquare ABCD)\)
para cualquier entero positivo\(n\). Por lo tanto,\(\text{area }[AB]\le 0\). Por otra parte, por definición de área\(\text{area }[AB]\ge 0\), de ahí
\(\text{area }[AB]= 0.\)
Para cualquier conjunto de un punto\(\{A\}\) tenemos eso\(\{A\}\subset [AB]\). Por lo tanto,
\(0\le \text{area }\{A\}\le \text{area }[AB]=0.\)
De dónde\(\text{area }\{A\}=0\).
Cualquier conjunto poligonal degenerado tiene área de fuga.
- Prueba
-
\(\mathcal P\)Sea un conjunto degenerado, digamos
Dado que el área es no negativa por definición, aplicando aditividad varias veces, obtenemos que
\(\begin{aligned} \text{area }\mathcal{P}\le & \text{area }[A_1B_1]+\dots+\text{area }[A_nB_n]+ \\ &+\text{area }\{C_1\}+\dots+\text{area }\{C_k\}.\end{aligned}\)
Por Proposición\(\PageIndex{1}\), el lado derecho se desvanece.
Por otro lado\(\text{area }\mathcal{P}\ge 0\), de ahí el resultado.
Decimos que conjunto poligonal\(\mathcal{P}\) se subdivide en dos conjuntos poligonales\(\mathcal{Q}_1,\dots,\mathcal{Q}_n\) si\(\mathcal{P}=\mathcal{Q}_1\cup\dots\cup \mathcal{Q}_n\) y la intersección\(\mathcal{Q}_i\cap\mathcal{Q}_j\) es degenerada para cualquier par\(i\) y\(j\). (Recordemos que según la reivindicación 20.3.1, las intersecciones\(\mathcal{Q}_i\cap\mathcal{Q}_j\) son poligonales.)
Supongamos que los conjuntos poligonales\(\mathcal{P}\) se subdividen en conjuntos poligonales\(\mathcal{Q}_1, \dots, \mathcal{Q}_n\). Entonces
\(\text{area }\mathcal{P}=\text{area }\mathcal{Q}_1+\dots+\text{area }\mathcal{Q}_n.\)
- Prueba
-
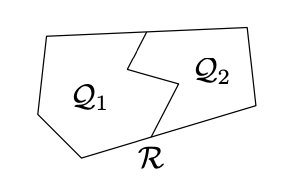
Asumir\(n=2\); por aditividad de área,
\(\text{area }\mathcal{P}=\text{area }\mathcal{Q}_1+\text{area }\mathcal{Q}_2-\text{area }(\mathcal{Q}_1 \cap\mathcal{Q}_2).\)
Dado que\(\mathcal{Q}_1\cap\mathcal{Q}_2\) es degenerado, por Corolario\(\PageIndex{1}\),
\(\text{area }(\mathcal{Q}_1\cap\mathcal{Q}_2)=0.\)
Aplicando esta fórmula algunas veces obtenemos el caso general. En efecto, si\(\mathcal{P}\) se subdivide en\(\mathcal{Q}_1,\dots,\mathcal{Q}_n\), entonces
\(\begin{aligned} \text{area }\mathcal{P}&=\text{area }\mathcal{Q}_1+\text{area }(\mathcal{Q}_2\cup\dots\cup\mathcal{Q}_n)= \\ &=\text{area }\mathcal{Q}_1+\text{area } \mathcal{Q}_2+\text{area }( \mathcal{Q}_3\cup\dots\cup\mathcal{Q}_n)= \\ &\ \ \ \vdots \\ &=\text{area }\mathcal{Q}_1+\text{area } \mathcal{Q}_2+\dots+\text{area }\mathcal{Q}_n.\end{aligned}\)
Dos conjuntos poligonales\(\mathcal{P}\) y se\(\mathcal{P}'\) denominan equidescomponibles si admiten subdivisiones en conjuntos poligonales\(\mathcal{Q}_1,\dots,\mathcal{Q}_n\) y\(\mathcal{Q}'_1,\dots,\mathcal{Q}'_n\) tal que\(\mathcal{Q}_i\cong\mathcal{Q}'_i\) para cada uno\(i\).
Según la proposición, si\(\mathcal{P}\) y\(\mathcal{P}\) son equidescomponibles, entonces\(\text{area } \mathcal{P}=\text{area }\mathcal{P}'\). También se mantiene lo contrario a esta afirmación; es decir, si dos conjuntos poligonales no degenerados tienen igual área, entonces son equidescomponibles.
El último comunicado fue probado por William Wallace, Farkas Bolyai y Paul Gerwien. La afirmación análoga en tres dimensiones, conocida como el tercer problema de Hilbert, es falsa; fue probada por Max Dehn.


