4.1: Geometría euclidiana
- Page ID
- 118039
Todo el resto de axiomas y definiciones (¡que siguen sin especificar!) de geometría neutra permanecen vigentes pero además añadimos:
Existe una línea y un punto no en esa línea tal que hay como máximo una línea en ese punto que es paralela a la línea original.
[Nota: Recordemos de geometría neutra que siempre tenemos al menos un paralelo así que ahora exactamente uno paralelo.]
Para cualquier línea y cualquier punto que no esté en esa línea, hay como máximo una línea en ese punto que es paralela a la línea original.
Estos dos axiomas son equivalentes.
Prueba: Obviamente, Global implica Local. Por el contrario, supongamos que Local es cierto. Entonces, dado que el caso de “no paralelos” no existe (estamos en geometría neutra), la negación de Global implicaría alguna línea y algún punto no en esa línea en la que había múltiples paralelos. Pero entonces la forma global del Postulado Paralelo Hiperbólico implicaría que la situación hiperbólica local dada debe ser cierta, la contradicción necesaria. QED.
La suma de los ángulos de un triángulo es igual a dos ángulos rectos. [Así que para un\(n\) -gon, exactamente\(180(n-2)\).]
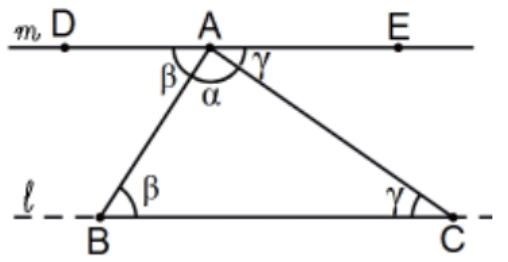
Prueba: Considera cualquier triángulo, digamos\(\triangle \mathrm{ABC}\). En A en AB, y en el lado opuesto, copie\(\angle A B C\), diga\(\angle D A B\), y en A en AC, y en el lado opuesto, copie\(\angle A C B\) para obtener\(\angle \mathrm{EAC}\). ¿Por qué la línea es\(\mathrm{DA}=\mathrm{AE}\) así\(\alpha+\beta+\gamma=180^{\circ}\)?
Si dos líneas paralelas son cortadas por una transversal, forman ángulos interiores alternados congruentes con la transversal [y alternan ángulos exteriores y ángulos correspondientes].
Prueba: PS 4, #2. Nota: Esto da otra prueba fácil del Teorema de la Suma de Ángulo: comience con el paralelo.
El área de cuadrado de longitud 1 unidad es 1 unidad cuadrada y, por extensión, el área de cualquier\(m \times n\) rectángulo es mn unidades cuadradas. El área de una región finita, acotada, simple (sin superposiciones), (en el plano) es el mayor límite inferior de las sumas de las áreas de todos los rectángulos que se pueden inscribir dentro de la región sin solapamiento de sus interiores siempre que el número sea igual al límite inferior superior de las sumas de las áreas de todos rectángulos que contienen la región sin solapamiento de sus interiores.
[Nota: Para probar que esta definición es significativa se requiere un análisis más real de lo que vamos a suponer.]
Dos triángulos son equivalentes si y sólo si tienen la misma área. De manera más general, un triángulo equivale a un\(n\) -gon iff tienen la misma área.
Prueba: No debería sorprender que el área se conservara bajo equivalencia pero ¿por qué no en geometría hiperbólica? Dicho esto, una prueba (solo para triángulos) es modificar el teorema correspondiente en geometría hiperbólica reemplazando cada ocurrencia de “suma angular” por “área” (PS 4, #28). ¿Existen pruebas menos sofisticadas? Absolutamente. Para otros polígonos, induce en el número de lados (PS 4, #33). (Esto no es cierto para la suma de ángulos en geometría hiperbólica). QED.
Fórmulas de área de polígonos ordinarios.
Si\(\triangle \mathrm{ABC}\) con lados\(\mathrm{a}, \mathrm{b}, \mathrm{c}\) es un triángulo rectángulo con ángulo recto en\(\mathrm{C}\), entonces\(\mathrm{a}^{2}+\mathrm{b}^{2}=\mathrm{c}^{2}\). Es decir, la suma de las áreas de los cuadrados en sus dos patas es igual al área del cuadrado en su hipotenusa.
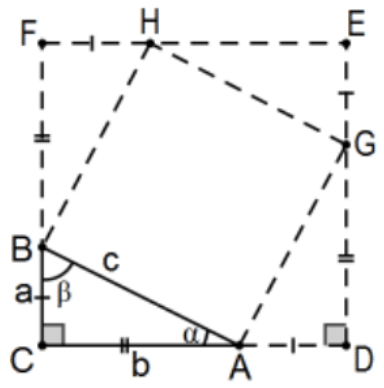
Prueba 1: Hay muchas pruebas de este resultado; algunas muy diferentes de otras. Entre los más fáciles está construir un cuadrado de lados\(a+b\) alrededor del triángulo y usar un poco de álgebra. Sumando las áreas de las piezas\((\mathrm{a}+\mathrm{b})^{2}=4((1 / 2) \mathrm{ab})+\mathrm{c}^{2}\) que tenemos que simplifica a:\(\mathrm{a}^{2}+\mathrm{b}^{2}=\mathrm{c}^{2}\). Los detalles se dejan como\(\mathrm{PS} 4\), #19. QED.
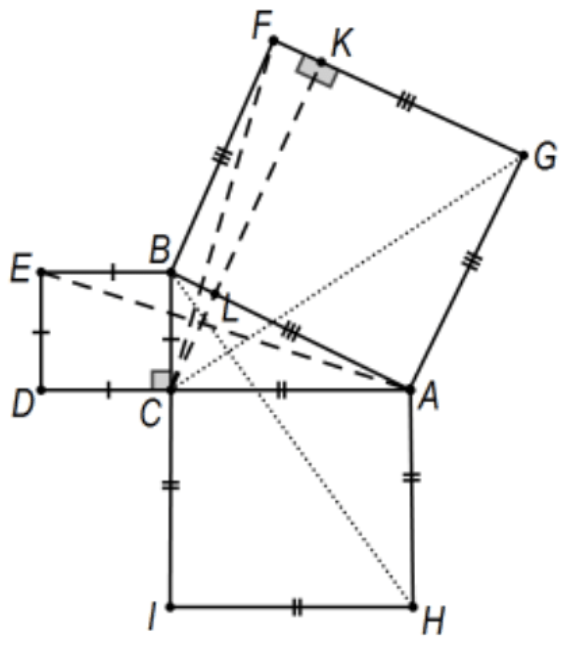
Prueba 2: Esta es la prueba tradicional de Euclides's Elements en el Libro 1, Prop 47 y todo prospectivo profesor de geometría de secundaria debe estar familiarizado con ella. Con un poco más de trabajo, se puede ajustar para probar que los cuadrados son equivalentes; es decir, los dos cuadrados más pequeños pueden ser “cortados” en un número finito de piezas y reordenados en los más grandes. En el triángulo rectángulo de la figura,\(\triangle \mathrm{ABC}\), con cuadrados a cada lado, se supone que las líneas auxiliares son como aparecen con CK determinada por la línea en\(C\) perpendicular a la hipotenusa\(A B\) del triángulo rectángulo original. El área de\(\triangle \mathrm{EBA}\) es la mitad del área del cuadrado pequeño BCDE (base BE y altura\(\mathrm{BC}\)) y, por SAS,\(\triangle \mathrm{EBA} \cong \triangle \mathrm{CBF}\) (rotar\(90^{\circ}\) aproximadamente por punto\(\mathrm{B}\)). Para el segundo triángulo, use base BF con altura BL. Así el BCDE cuadrado tiene la misma área que el rectángulo BFKL. Por simetría, (segmentos BH y\(\mathrm{CG}\)) cuadrado\(\mathrm{ACIH}\) y rectángulo\(\mathrm{AGKL}\) tienen la misma área. QED.
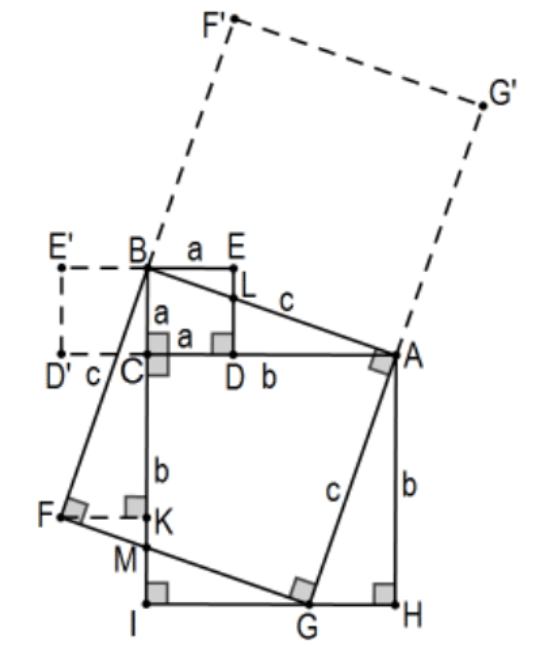
Prueba 3: Mucho más fácil es una prueba que demuestra directamente que los dos cuadrados más pequeños son equivalentes al más grande. En esta, dobla el cuadrado sobre una pata para superponer el triángulo y doblar el cuadrado sobre la hipotenusa tanto a través del triángulo como de los cuadrados adyacentes. Obsérvese eso\(\mathrm{D}^{\prime}, \mathrm{E}^{\prime}, \mathrm{F}^{\prime}\), y no\(\mathrm{G}^{\prime}\) forman parte de la prueba; sólo están ahí para ayudar a visualizar la situación en su forma tradicional. Sorprendentemente, esto requiere solo una línea auxiliar\(\mathrm{FK}\),, donde\(\mathrm{K}\) está la\(\mathrm{F}\) perpendicular en línea\(\mathrm{BC}\). La idea es mostrar que el cuadrado en\(\mathrm{BC}\left(\mathrm{a}^{2}\right)\) junto con el cuadrado en\(\mathrm{AC}\left(\mathrm{b}^{2}\right)\) es equivalente al cuadrado en\(\mathrm{AB}\left(\mathrm{c}^{2}\right)\). Dado que hay tanto solapamiento, la equivalencia sólo requiere confirmar eso\(\triangle \mathrm{AGH} \cong \triangle \mathrm{BFK}\),\(\triangle \mathrm{BLE} \cong \triangle \mathrm{FMK}\),\(\triangle \mathrm{ALD} \cong \triangle \mathrm{GMI}\) y eso\(\mathrm{G}\) es colineal con\(\mathrm{H}\) y I. Los detalles se dejan como PS 4, #20. QED.
Otras pruebas se dan en PS 4, #21 -24.
Si\(\triangle \mathrm{ABC}\) es tal que\(\mathrm{a}^{2}+\mathrm{b}^{2}=\mathrm{c}^{2}\), entonces es un triángulo rectángulo con ángulo recto en\(\mathrm{C}\).
Prueba: Construir un triángulo rectángulo con patas de tamaño a y b. según el Teorema de Pitágoras, el tercer lado es...? Entonces por SSS...? QED.
El segmento que une los puntos medios de dos lados de un triángulo es la mitad de la longitud del tercer lado y paralelo a éste.
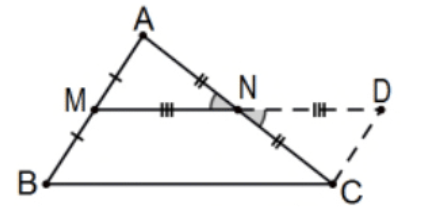
Prueba: Dejar\(\mathrm{M}\) y\(\mathrm{N}\) ser los puntos medios de los segmentos\(\mathrm{AB}\) y\(\mathrm{AC}\) de\(\triangle \mathrm{ABC}\) y doble segmento\(\mathrm{MN}\) a determinar\(\mathrm{D}\) como se indica. Con los ángulos verticales en\(\mathrm{N}\) que tenemos\(\triangle \mathrm{CND} \cong \triangle \mathrm{ANM}\) por SAS. Entonces\(\mathrm{AM} \cong \mathrm{CD}\) y\(\angle \mathrm{DCN} \cong \angle \mathrm{A}\) por cpctc y tenemos congruentes ángulos interiores alternos por lo que las líneas\(\mathrm{AM}=\mathrm{BM}\) y\(\mathrm{CD}\) son paralelas. Con\(\mathrm{AM} \cong \mathrm{BM}\) eso\(\mathrm{BM} \cong \mathrm{CD}\), tenemos BCDM cuadrilátero con un par de lados opuestos que son a la vez paralelos y congruentes. Ya que estamos en geometría euclidiana, el cuadrilátero es un paralelogramo (PS 4, #15) por lo que sus lados opuestos son congruentes (PS 4, #12). Es decir, MD\(\cong B C\) y, ya que\(\mathrm{MN} \cong \mathrm{ND}\) por construcción,\(\mathrm{N}\) es el punto medio del segmento MD conocido por ser congruente con BC. Por lo tanto, tenemos el segmento MN paralelo y la mitad del segmento BC según se requiera. QED.
Dos polígonos son similares (se indica ““), y la correspondencia una similitud, si (así iff) hay una correspondencia proporcional entre sus lados que preserva sus ángulos; es decir, una correspondencia 1-1 de los lados de uno a otro con un número real positivo r, el relación común, tal que la longitud del segundo es la longitud del primero multiplicada por\(\mathrm{r}\) y el ángulo entre dos lados correspondientes no se modifica.
Por ejemplo,\(\triangle\) MAN\(\sim \triangle B A C\) con\(r=2\) en el último teorema ya que los otros dos pares de ángulos son congruentes porque las líneas son paralelas. Aún más trivialmente, las cifras congruentes son similares con relación común\(r=1\).
Si dos triángulos son tales que las relaciones entre dos de sus lados son iguales y los ángulos entre esos dos pares de lados son congruentes, entonces los triángulos son similares.orem texto
Prueba: En primer lugar, esto parece que nuestra proporción es incorrecta porque esto habla de la relación de dos lados del mismo triángulo en lugar de la presencia de una constante de proporcionalidad para la correspondencia (longitud lateral de imagen a longitud lateral original). Este hecho se debe a la propiedad de las fracciones ordinarias:
\(a / b=x / y\)si sus\(a / x=b / y\) recíprocos están de acuerdo; es decir,\(x / a=y / b\).
Aquí, pensemos\(x\) como la longitud de la imagen del lado de longitud\(a\), y de\(y\) igual manera para\(b\), y bajo la correspondencia que, esperamos, resulta ser una correspondencia de similitud. \(r\)Sea esa relación común; es decir,\(r=x / a\) o\(x=r a\) y\(y=r\) b. A probar es que, para cualquiera\(r>0\), los otros 2 ángulos también son congruentes y los terceros lados están en la misma proporción\(\mathrm{r}\). La prueba se basa en la inducción\(\mathrm{r}=\mathrm{n}\) como números naturales y fracciones simples\(r=1 / n\) con el nuevo triángulo con dos lados y ángulo incluido superpuesto sobre el original\(\triangle \mathrm{ABC}\) (por SAS para triángulos congruentes) con los dos lados de longitud \(\mathrm{r}(\mathrm{AB})\)y\(r(\mathrm{AB})\).
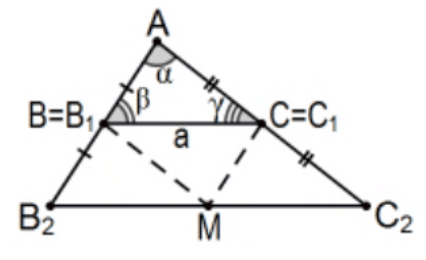
Caso\(\mathrm{r}=1\): Esto es solo Congruencia SAS como se mencionó anteriormente.
Caso\(\mathrm{r}=2\): Esto es solo una consecuencia inmediata del último teorema. Con el fin de prepararse para una prueba por inducción matemática, renombramos los vértices como se muestra en la imagen, con puntos medios\(\mathrm{B}=\mathrm{B}_{1}\) y\(\mathrm{C}=\mathrm{C}_{1}\) haciendo longitudes\(\mathrm{AB}_{2}=2 \mathrm{AB}\) y\(\mathrm{AC}_{2}=2 \mathrm{AC}\). Por el último teorema, la longitud de\(\mathrm{B}_{2} \mathrm{C}_{2}=2 \mathrm{~B}_{1} \mathrm{C}_{1}\) y la línea\(\mathrm{B}_{2} \mathrm{C}_{2}\) paralela a la línea\(\mathrm{B}_{1} \mathrm{C}_{1}\) confirmando\(\angle \mathrm{AB}_{1} \mathrm{C}_{1} \cong \angle \mathrm{AB}_{2} \mathrm{C}_{2}\) y\(\angle \mathrm{AC}_{1} \mathrm{~B}_{1} \cong \angle \mathrm{AC}_{2} \mathrm{~B}_{2}\). Dejar\(M_{2}\) ser el punto medio del segmento\(B_{2} C_{2}\) determina 3 nuevos triángulos todos congruentes con los triángulos originales\(\triangle A B C\) y\(4=2^{2}\) congruentes.
Caso\(r=1 / 2\): Esta vez, intercambiar el triángulo inicial\(B=B_{2}\) y\(C=C_{2}\) hacer longitudes\(A B_{1}=(1 / 2) A B\) y\(\mathrm{AC}_{1}=(1 / 2) \mathrm{AC}\), la situación de punto medio del teorema motivador anterior.
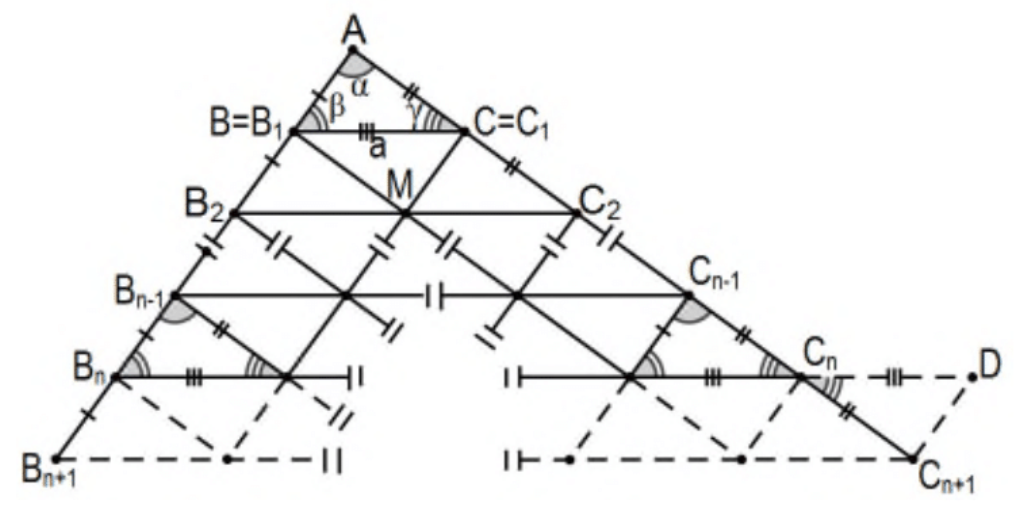
Caso\(r=n\): Para\(n\) cualquier entero positivo, induzca\(n\) más allá del caso de\(r=2\) lo siguiente:
Supongamos que el resultado (similitud\(\mathrm{r}=\mathrm{n}\) con el factor común con triángulos congruentes\(\mathrm{n}^{2}\) internos) es válido\(r=2,3, \ldots, n\) y considera cualquier triángulo\(\triangle \mathrm{AB}_{\mathrm{n}+1} \mathrm{C}_{\mathrm{n}+1}\) con longitud\(\mathrm{AB}_{\mathrm{n}+1}=(\mathrm{n}+1) \mathrm{AB}\)\(\mathrm{AC}_{\mathrm{n}+1}=(\mathrm{n}+1) \mathrm{AC}\), longitud y, por conveniencia, la misma LA. Por el Postulado Regla, identificar n puntos para determinar segmentos\(n+1\) congruentes a lo largo de cada segmento\(\mathrm{AB}_{\mathrm{n}+1}\) y\(\mathrm{AC}_{\mathrm{n}+1}\) por número de subíndice y aplicar la hipótesis inductiva a\(\triangle \mathrm{AB}_{\mathrm{n}} \mathrm{C}_{\mathrm{n}}\). Siguiendo la prueba del teorema anterior, extender segmento\(B_{n} C_{n}\), de longitud\(n B C\) por la hipótesis inductiva, por un segmento de longitud\(B C\) para determinar punto\(D\) y considerar\(\Delta C_{n+1} D C_{n}\). Este triángulo es congruente con el original,\(\Delta C_{n+1} C_{n} D \cong \Delta A C B\) por SAS. Por cpctc de segmentos y ángulos y transitividad,\(\mathrm{DC}_{n+1} \cong \mathrm{B}_{\mathrm{n}} \mathrm{B}_{\mathrm{n}+1}\) y sus líneas son paralelas por lo que el cuadrilátero\(\mathrm{B}_{\mathrm{n}} \mathrm{B}_{n+1} C_{n+1} \mathrm{D}\) tiene un par de lados opuestos que son a la vez congruentes y paralelos por lo que es un paralelogramo (PS 4, #15) y su otro par de lados opuestos también son congruentes y paralelo\((\mathrm{PS} 4, \# 12)\). Dado que\(\mathrm{B}_{\mathrm{n}} \mathrm{D}\) es de longitud\(\mathrm{nBC}+\mathrm{BC}=(\mathrm{n}+1) \mathrm{BC}\), el lado necesario también\(\mathrm{B}_{\mathrm{n}+1} C_{\mathrm{n}+1}\) está junto con la congruencia apropiada de los ángulos en\(\mathrm{B}_{\mathrm{n}+1}\) y\(\mathrm{C}_{\mathrm{n}+1}\) confirmando similitud con\(\Delta \mathrm{ABC}\). Finalmente, contando el número de los triángulos congruentes internos, tenemos los originales\(n^{2}\) más los\(n+1\) nuevos orientados con\(\triangle \mathrm{ABC}\) y\(n\) entre ellos orientados al revés:\(n^{2}+(n+1)+n=n^{2}+2 n+1=(n+1)^{2}\) y el paso inductivo es completo. (Para una mejor comprensión, siga cuidadosamente la prueba con\(n=3\); las ideas son exactamente las mismas).
Caso\(\mathrm{r}=1 / \mathrm{n}\): Para cualquier entero positivo\(\mathrm{n}\) y dos triángulos que satisfagan las condiciones SAS para Similaridad con relación común\(\mathrm{r}=1 / \mathrm{n}\) (un par de ángulos congruentes y ahí incluyendo pares de lados en la misma\(1 / \mathrm{n}\) proporción), dividir cada uno de los incluyendo los lados del triángulo más grande, digamos\(\triangle \mathrm{ABC}\) en segmentos\(\mathrm{n}\) congruentes (Postulado Regla) e indexarlos como con la prueba de cualquier número natural\(r=n ;\) que sea\(B_{n}=B\) y\(C_{n}=C\) y cada punto de esos subdivisiones como\(\mathrm{B}_{\mathrm{i}}\) y\(\mathrm{C}_{\mathrm{i}}\) a lo largo del camino. Entonces por\(\mathrm{SAS}\) Congruencia, el más pequeño de los triángulos es congruente a\(\Delta \mathrm{AB}_{1} \mathrm{C}_{1}\) partir de lo cual podemos recuperar similitud con el original\(\Delta \mathrm{ABC}\) por el caso de\(r=n\).
Caso\(r=m / n:\) Para cualquier número racional positivo: En este caso, comience ya sea con el numerador o el denominador y aplique los casos apropiados en secuencia.
Caso\(\mathrm{r}:\) Para cualquier número real positivo\(\mathrm{r}:\) Si\(\mathrm{r}\) es racional, ya se hace así que asuma\(\mathrm{r}\) es irracional. Considere cualquier secuencia de números racionales positivos que converja\(r\) y utilice la continuidad. \(Q E D\)
Si dos triángulos son tales que la relación entre los tres pares de sus lados correspondientes es la misma, entonces los triángulos son similares.
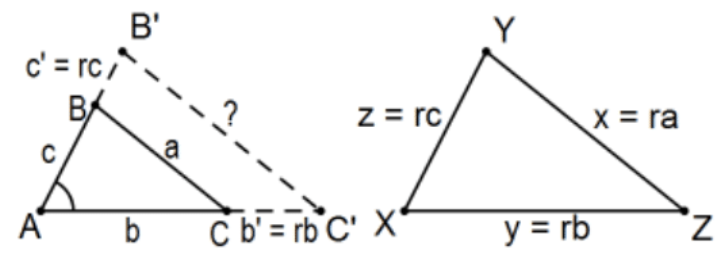
Prueba: Aquí la constante de proporcionalidad para la correspondencia es esa proporción común\(r\). Sería posible comenzar de cero como en la prueba de SAS Similitud pero no es necesario. Elige dos de los lados del primer triángulo y considera el triángulo formado por el ángulo entre ellos pero con los dos lados r veces más largos. Por SAS Similitud, el tercer lado de ese triángulo es\(r\) multiplicado por el tercer lado original, ra. Pero entonces, por Congruencia SSS,... QED.
Si dos triángulos son tales que dos de sus ángulos son congruentes, entonces los triángulos son similares.
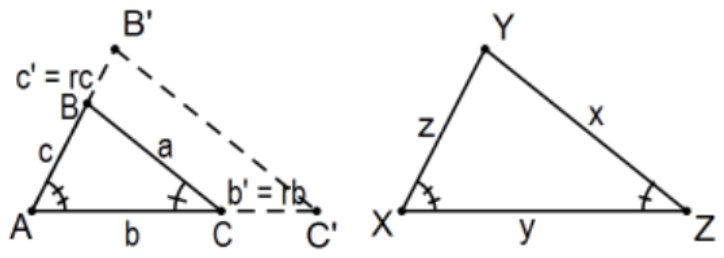
Prueba: ¿Dónde está la constante de proporcionalidad para la correspondencia? Es la relación r de los lados incluidos por los dos pares de ángulos congruentes,\(r=y / b\).
Dado que sólo hay un par de bandos bajo consideración, “ellos” todos están de acuerdo y proceden como con SSS como arriba. De manera más explícita, supongamos\(\triangle \mathrm{ABC}\) y\(\triangle \mathrm{XYZ}\) son tales que\(\angle \mathrm{A} \cong \angle \mathrm{X}\) y\(\angle \mathrm{C} \cong \angle \mathrm{Z}\) como se indica. Multiplicando los 2 lados de\(\angle A\) por el mismo factor\(r\)\(\mathrm{r}>0\),, tenemos triángulos similares\(\triangle \mathrm{ABC} \sim \triangle \mathrm{AB}^{\prime} \mathrm{C}^{\prime}\) por\(\mathrm{SAS}\) similitud. Por definición de similitud,\(\angle \mathrm{C}^{\prime} \cong \angle \mathrm{C}\) entonces, por transitividad,\(\angle \mathrm{C}^{\prime} \cong \angle \mathrm{Z}\) y tenemos\(\triangle \mathrm{AB}{ }^{\prime} \mathrm{C}^{\prime} \cong \triangle \mathrm{X} \mathrm{YZ}\) por congruencia ASA. Por último,\(\triangle \mathrm{ABC} \sim \triangle \mathrm{XYZ}\) por transitividad.
La altitud desde el ángulo recto de un triángulo rectángulo divide el triángulo en dos triángulos cada uno similar al original.
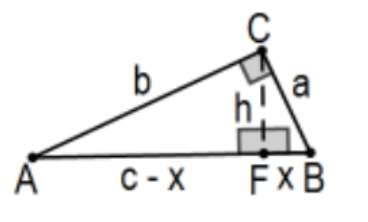
Prueba: Los ángulos agudos de un triángulo rectángulo son complementarios por lo que el resultado es inmediato por similitud AA. QED.
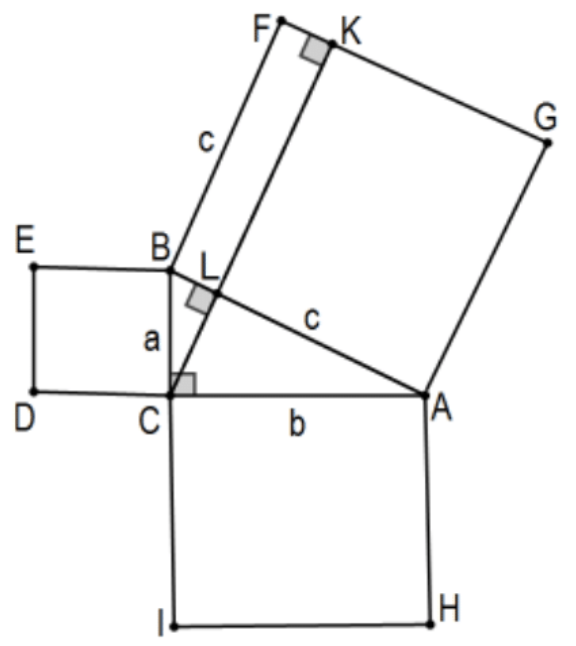
Prueba 4: Este hecho da el corazón de otra prueba más del Teorema de Pitágoras; agradable en que tiene el cuadro tradicional pero con una prueba mucho más fácil. Comenzando como antes con derecha\(\triangle \mathrm{ABC}\) con un cuadrado a cada lado, tomar la línea en el vértice de ángulo recto\(C\) perpendicular a la hipotenusa para que\(\mathrm{CL}\) sea la altitud desde el ángulo recto de derecha\(\triangle \mathrm{ABC}\). Eso implica eso\(\mathrm{BL} / \mathrm{a}=\mathrm{a} / \mathrm{c}\) para que\(\mathrm{c}(\mathrm{BL})=\mathrm{a}^{2}\). Es decir, el área de cuadrado\(\mathrm{BCDE}\) es el área del rectángulo BFKL. Del mismo modo\(\mathrm{b}^{2}\) es el área del rectángulo AGKL. QED. (ver\(\operatorname{PS} 4, \# 21)\)
[Más explícitamente, las longitudes de los segmentos de 2 transversales a 3 (o más) líneas paralelas son proporcionales (tienen las mismas proporciones)].
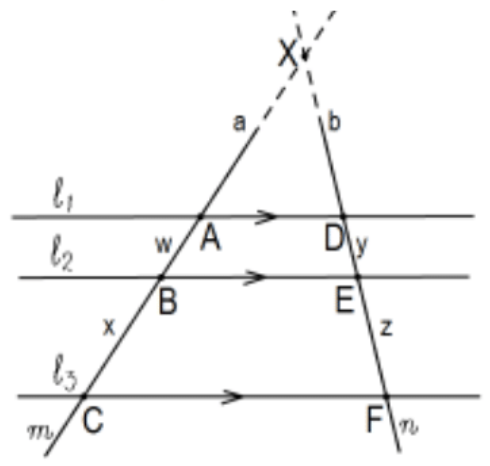
Prueba: En la figura, las 3 líneas\(\ell_{1}, l_{2}\), y\(l_{3}\) son líneas paralelas cortadas por transversales\(m\) y\(n\). Necesitamos demostrar que los segmentos determinados son proporcionales; es decir, mostrar eso\(w / x=y / z\).
Si las transversales\(m\) y\(n\) son paralelas, los cuadriláteros determinados son paralelogramos así\(\mathrm{w}=\mathrm{y}\)\(\mathrm{x}=\mathrm{z}\) y la igualdad trivial de las proporciones asumen que se cruzan. Que X sea la intersección de\(m\) y\(n\). Eso determina 3 triángulos, todos similares por similitud AA. La igualdad de las relaciones deseadas se deriva de la aplicación directa de las relaciones de similitud de estos triángulos. Los detalles se dejan como PS 4, #18.
Constructo: El producto y el cociente de dos segmentos lineales.
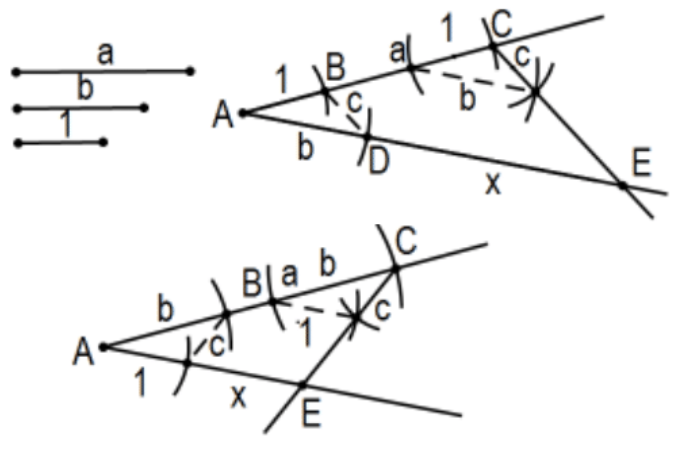
Más específicamente, dados los segmentos de línea de longitudes a\(b\), y la longitud unitaria 1, construyen segmentos de longitud ab y\(a / b\). y\(\mathrm{D}\) como se indica en la figura determina\(\triangle \mathrm{ABD}\). Copia\(\angle \mathrm{B}\) en el punto\(\mathrm{C}\) como se indica para determinar el punto\(\mathrm{E}\) en el otro rayo. Entonces\(\mathrm{x}\), la longitud del segmento\(\mathrm{DE}\), es la longitud requerida,\(x=a b\). Para a/b, es la misma construcción excepto comenzar con el b seguido de a en un rayo y el 1 en el otro rayo.
Prueba: Por construcción,\(\angle \mathrm{ABD} \cong \angle \mathrm{ACE}\) y congruentes ángulos correspondientes implica que las líneas CE y BD son paralelas. Dado que las líneas paralelas cortan segmentos proporcionales,\(1 / b=a / x\). Por lo tanto\(x=a b\).
Teorema: La bisectriz de un ángulo de un triángulo divide el lado opuesto proporcionalmente con los lados del ángulo.
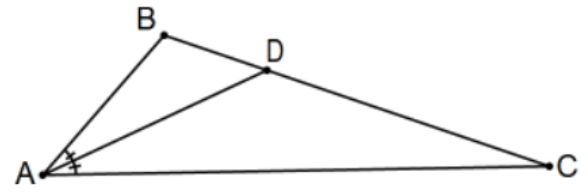
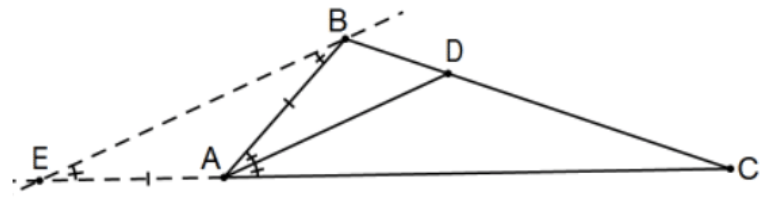
Es decir, en la figura asociada, si el rayo\(\mathrm{AD}\) es la bisectriz de\(\angle A\), entonces\(\mathrm{AB} / \mathrm{AC}=\mathrm{DB} / \mathrm{DC}\).
Prueba: Dejar\(\mathrm{E}\) ser la intersección de la línea AC con la línea en\(\mathrm{B}\) paralelo a línea\(\mathrm{AD}\) y considerar el triángulo creado:\(\triangle \mathrm{DCA} \sim \triangle \mathrm{BCE}\). QED.
Corolario: La bisectriz de un ángulo de un triángulo es una mediana si y solo si el triángulo es isósceles.
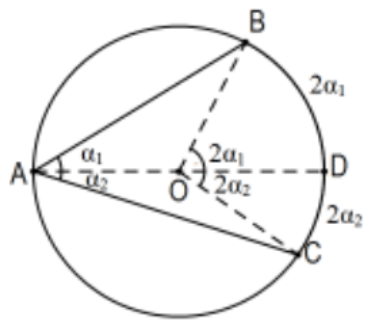
Teorema: Teorema de Ángulo Inscrito: Un ángulo inscrito en un círculo tiene medida la mitad de la medida de su arco interceptado (subtendido); es decir, la mitad de la de su ángulo central correspondiente.
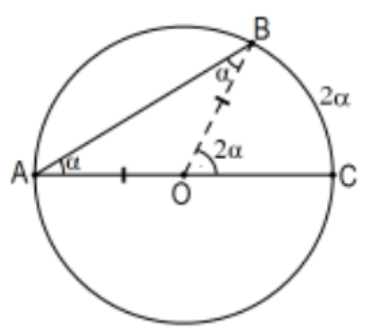
Prueba: En todos los casos, el vértice\(A\) está en el círculo con el centro en\(O\).
Caso 1: Un lado del ángulo es un diámetro. En este caso, el ángulo central es exactamente el ángulo exterior del triángulo isósceles determinado por el ángulo inscrito. De manera explícita, ya que\(\mathrm{OA}\) y\(\mathrm{OB}\) son radios del mismo círculo,\(\triangle \mathrm{AOB}\) es isósceles y sus ángulos de base (at\(A\) y\(B\)) son congruentes de manera que su suma es dos veces\(\alpha=m(\angle A)\). Por la forma euclidiana del EAT,\(2 \alpha=2 \mathrm{~m}(\angle \mathrm{A})=\mathrm{m}(\angle \mathrm{BOC})\). Dado que la medida del arco se define como la medida del ángulo central que la subtiende, se prueba la aserción.
Caso 2: El centro del círculo es interior al ángulo. Incluye diámetro OD:\(2 \alpha=2\left(\alpha_{1}+\alpha_{2}\right)=2 \alpha_{1}+2 \alpha_{2}\).
Caso 3: El centro del círculo es exterior al ángulo.
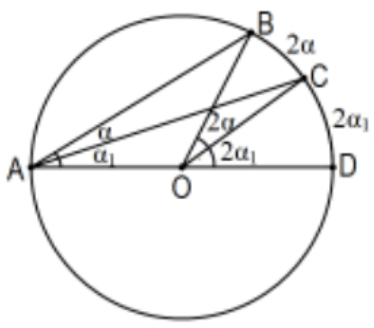
Tenga en cuenta que\(\angle B A C=\angle B A D-\angle C A D\). Esto implica que\(2 \alpha=2\left(\left(\alpha+\alpha_{1}\right)-\alpha_{1}\right)=2\left(\alpha+\alpha_{1}\right)-2 \alpha_{1}\).
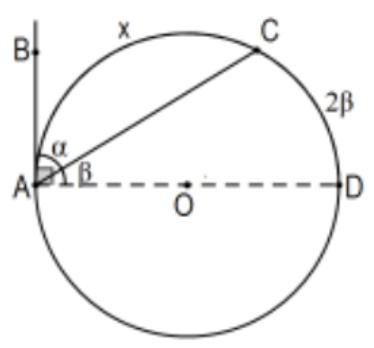
Caso 4: Un lado del ángulo es tangente al círculo. Supongamos que la línea\(\mathrm{AB}\) es tangente al círculo en\(\mathrm{A}\), y que\(\angle B A C\) es aguda. Considerar\(\angle C A D\), el ángulo complementario con el diámetro\(\mathrm{AD}\) determinado por el radio\(\mathrm{OA}\) ya que, por teorema anterior, las líneas\(\mathrm{AB}\) y\(\mathrm{AD}\) son perpendiculares. Obviamente, la medida del arco AC es\(\mathrm{x}=180^{\circ}-\mathrm{m}(\operatorname{arc} \mathrm{CD})\) así, por el Caso 1,\(x=180^{\circ}-2 \beta=2\left(90^{\circ}-\beta\right)=2 \alpha\) y ya terminamos. Si\(\angle B A C\) es obtuso, su suplemento es agudo así que usa el caso agudo y resta de\(360^{\circ}\).
Corolario: Un triángulo inscrito en un semicírculo (es decir, un lado es un diámetro) es un triángulo rectángulo.
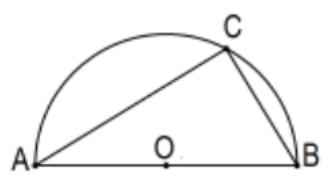
Históricamente, este hecho es conocido como el Teorema de Thales. Thales fue un matemático filósofo que vivió aproximadamente 300 años antes de Euclides y ha sido llamado el primer filósofo de la tradición griega.
Corolario: Construye las tangentes desde un punto fuera de un círculo hasta el círculo.
[Nota: Esto fue PS 2, #25, en geometría neutra. ¿Por qué volver a hacerlo? Esta construcción es la que suele enseñarse por lo que es mucho más conocida que la anterior. Esta situación es un poco extraña ya que ambas construcciones están en el Euclides original, Libro III, la geometría neutra es más fácil de probar, y se da antes (Prop. 17 versus Prop. 31). Hace un buen ejemplo, sin embargo, de una situación en la que cambiar los axiomas deja verdadera la proposición (la capacidad de construir las tangentes) pero la forma euclidiana dada aquí no es válida en geometría neutra. Los pasos de la construcción se pueden hacer pero, no solo falla la prueba, ¡nunca produce las tangentes reales!]
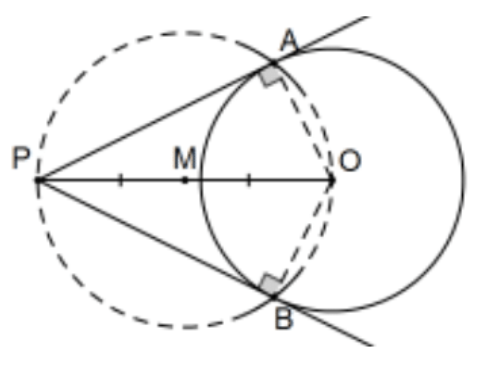
Construcción: Bisecar el segmento determinado por el punto y el centro del círculo y considerar el círculo centrado en ese punto con radio determinado por cualquiera de esos puntos, (M; MO). Sus intersecciones con el círculo son los puntos de tangencia. Más explícitamente, (si no se da el centro del círculo) construir el centro del círculo,\(\mathrm{O}\), el punto medio del segmento\(\mathrm{M}\) de línea PO, y el círculo con centro en M y radio MP = MO. Dejando\(A\) y\(B\) siendo los puntos de intersección de este círculo con el círculo original, las líneas PA y PB son las tangentes deseadas.
Prueba: Esto es inmediato del teorema sobre triángulos inscritos en semicírculos. QED.
Teorema: Construir un segmento de línea de longitud la raíz cuadrada de la longitud de un segmento:
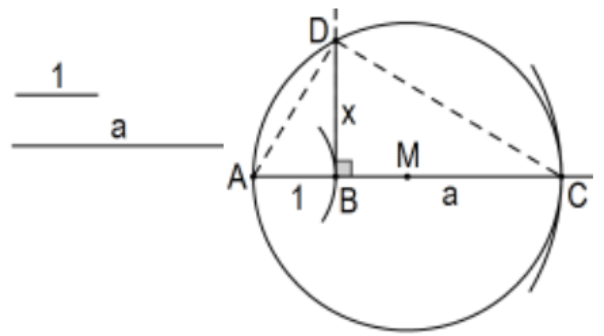
Solución: Dados segmentos de unidad de longitud y longitud a\(M\), constructo, el punto medio de un segmento de longitud\(1+\mathrm{a},(\mathrm{AB}+\mathrm{BC}=\mathrm{AC}\) en la figura\()\), y el círculo centrado en\(M\) de radio\(M C\). Finalmente, construya la perpendicular en el punto\(B\) para determinar el punto\(D\). Entonces el segmento BD es el segmento requerido.
Prueba: Se trata de un triángulo inscrito en un semicírculo así\(\triangle \mathrm{ACD}\) es un triángulo rectángulo y\(\mathrm{BD}\) es la altitud desde el ángulo recto así\(\triangle \mathrm{ADB} \sim \triangle \mathrm{DCB}\) y tenemos\(x / 1=a / x\) así que eso\(x^{2}=a\) o\(x=\sqrt{a}\). QED.
Teorema: Construir la media geométrica de las longitudes de dos segmentos de línea:
Es decir, dados los segmentos de longitudes a y\(b\), resuelven:\(x^{2}=a b\) geométricamente.
Solución: Comience con\(\mathrm{m}(\mathrm{AB})=\mathrm{a}\) y\(\mathrm{m}(\mathrm{BC})=\mathrm{b}\) en la figura anterior. QED.
Construir todas las soluciones positivas de una ecuación cuadrática: Es decir, si a, b y c son constructibles y la ecuación tiene soluciones reales, resuelva\(a x^{2}+b x+c=0\) geométricamente.
Solución: Para\(a x^{2}+b x+c=0, a \neq 0\), recordemos que la fórmula cuadrática da a sus soluciones:
\(x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a} \quad\)Cada paso del algoritmo es construible. QED.
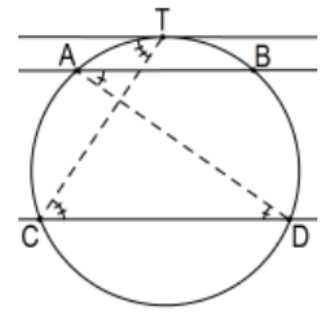
Teorema: Las líneas paralelas que intersectan un círculo determinan los arcos congruentes.
Prueba: Esto es inmediato del Teorema del Ángulo Inscrito.
Nota: Hay un problema en que nunca hemos discutido lo que significa incluso arcos congruentes; todo ha sido en términos de romper una figura en triángulos congruentes lo cual es imposible para arcos de círculos. Obviamente, los círculos congruentes son aquellos con radios congruentes. Para arcos congruentes, nos referimos a arcos de círculos congruentes que determinan ángulos centrales congruentes o equivalentemente (por congruencia SAS de triángulos) acordes congruentes.
[Nota: Esto NO es cierto en geometría hiperbólica: (arco Poincaré: DC\(\cong \mathrm{AB}<\mathrm{EB}\)).]
Teorema: El teorema del acorde: Para un punto dentro de un círculo, el producto de las longitudes de los segmentos determinados en cualquier acorde a través de él es constante (es decir,\(w x=y z\) en la figura), y la medida de un ángulo determinado por dos acordes a través del punto es la mitad de la suma de su interceptado arcos (subtendidos).
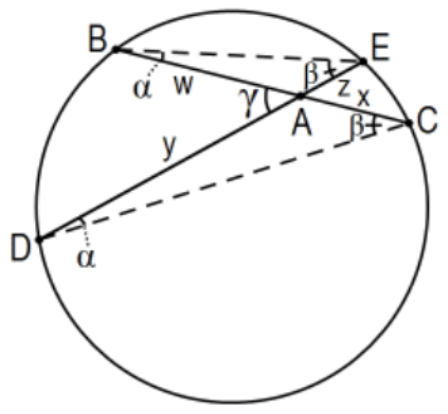
Prueba: Por el Teorema del Ángulo Inscrito,\(\angle \mathrm{E} \cong \angle \mathrm{C}\) y\(\angle \mathrm{B} \cong \angle \mathrm{D}\) así, por Similitud AA,\(\triangle \mathrm{ABE} \sim \triangle \mathrm{ADC}\) así\(\mathrm{AB} / \mathrm{AD}=\mathrm{AE} / \mathrm{AC}\) o\(\mathrm{w} / \mathrm{y}=\mathrm{z} / \mathrm{x}\). Por último,\(\mathrm{wx}=\mathrm{yz}\). Para los ángulos,\(\mathrm{m}(\angle \mathrm{BAD})=\mathrm{m}(\angle \mathrm{ABE})+\mathrm{m}(\angle \mathrm{AEB})\) por la forma euclidiana del EAT y utilizar el Teorema del Ángulo Inscrito para expresar\(\mathrm{m}(\angle \mathrm{ABE})\) y\(\mathrm{m}(\angle \mathrm{AEB})\) en términos de las medidas de arco de sus arcos subtendidos. QED.
Para un punto fuera de un círculo, el producto de las longitudes del segmento externo multiplicado por toda su secante (segmento externo más la cuerda) es constante y en el caso tangente esa constante es solo el cuadrado de la longitud del segmento. La medida del ángulo en el punto determinado por dos secantes es la mitad de la diferencia de los arcos subtendidos. Eso es y como se muestra en la foto, incluyendo el caso tangente,\(\mathrm{w}(\mathrm{w}+\mathrm{x})=\mathrm{y}(\mathrm{y}+\mathrm{z})=\mathrm{t}^{2}\).
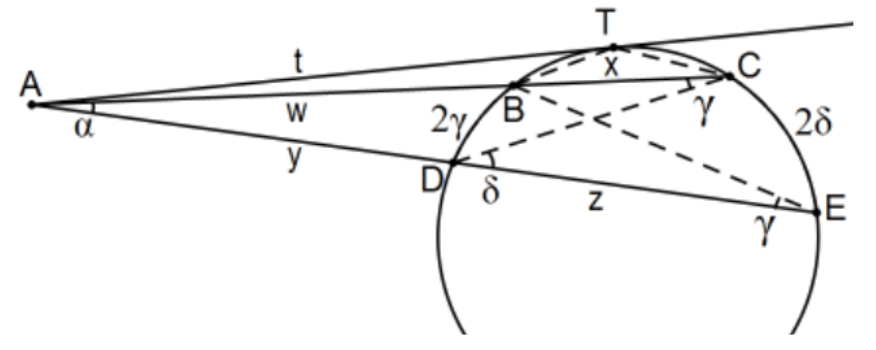
Prueba: El ángulo a\(A\) es en común y, por el Teorema del Ángulo Inscrito,\(\angle C \cong \angle \mathrm{E}\) así tenemos\(\triangle \mathrm{ABE} \sim \triangle \mathrm{ADC}\) por similitud AA. Para la conclusión constante del producto,\(\mathrm{AB} / \mathrm{AE}=\mathrm{AD} / \mathrm{AC}\) y cruzar multiplicar. Para los ángulos, use la forma euclidiana del\(\mathrm{ETA}, \mathrm{m}(\angle \mathrm{CDE})=\mathrm{m}(\angle \mathrm{DAC})+\mathrm{m}(\angle \mathrm{DCA})\), o\(\delta=\alpha+\gamma\) o\(\alpha=\delta-\gamma\). Ahora por el Teorema de Ángulo Inscrito con arcos\(C E\) y BD, tenemos\(\delta=(1 / 2)(\mathrm{m}(\mathrm{CE})-\mathrm{m}(\mathrm{BD}))\). Para el caso de tangente, ver\(\mathrm{PS} 4, \# 7\) QED.
De vuelta en el Capítulo 1, aprendimos a construir el centro de un círculo en geometría neutra; es decir, elegir tres puntos cualesquiera del círculo y los bisectores perpendiculares de dos acordes cualesquiera determinados se cruzan para determinar el centro del círculo. Esta construcción era familiar para muchos de ustedes como construcción para el círculo circular de un triángulo. Es decir, construir los bisectores perpendiculares de dos de los lados del triángulo para determinar el circuncírculo y el segmento desde ese punto a cualquiera de sus vértices es su radio. Vimos en el Capítulo 3 que no es válido en geometría neutra porque es falso en geometría hiperbólica; es decir, sabemos que algunos triángulos no tienen circuncírculo porque a veces esos bisectores perpendiculares no se cruzan. En el caso euclidiano, la falta de intersección implicaría que los dos lados elegidos formaban parte de la misma línea de manera que el triángulo no era un triángulo sino un triángulo llamado “degenerado”; es decir, tres puntos colineales. Polígonos con más de tres lados, sin embargo, no son tan claros; generalmente un polígono no tiene circuncírculo pero hay una caracterización sorprendente para cuadriláteros:
Un cuadrilátero tiene un circuncírculo si y solo si cada par de ángulos opuestos tiene la suma de\(180^{\circ}\).
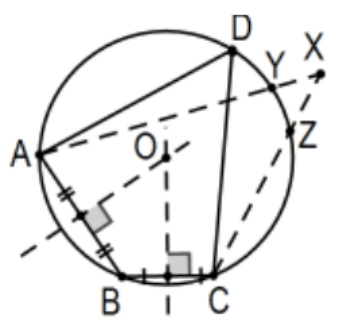
Prueba: El teorema del ángulo inscrito implica inmediatamente que si un cuadrilátero se puede inscribir en un círculo, los ángulos opuestos deben sumarse a\(180^{\circ}\). Por el contrario, supongamos que tenemos cuadriláteros con ángulos opuestos que se suman a\(180^{\circ}\). Usa cualquiera de los tres vértices para construir el circuncírculo de ese triángulo, el triángulo esos tres puntos determinan y prueban que el cuarto vértice debe estar sobre él también. En esencia, el teorema del acorde (si el punto estuviera dentro) y el teorema secante (si el punto estuviera afuera) implicarían que la suma del ángulo estaría equivocada. Los detalles se dejan como Ex\(30.\)
Constructo: El producto y el cociente de dos segmentos de línea usando el teorema de acordes:
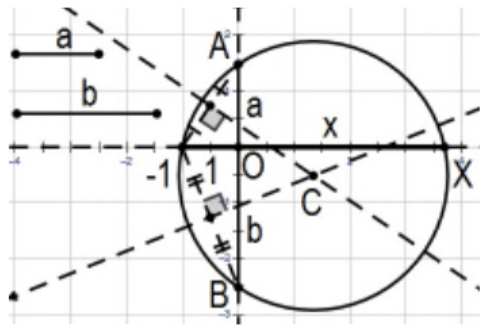
Una construcción alternativa para el producto (y para el cociente) de las longitudes de dos segmentos de línea de longitudes dadas es comenzando con dos líneas que se cruzan como las líneas de sus acordes eventuales con la suma construida de los segmentos de la intersección de las líneas como uno de los acordes y un segmento de unidad de longitud desde ese punto como un segmento de la otra cuerda. Eso determina 3 puntos del círculo deseado y utilizarlos para construir el círculo determinado. La longitud del segmento desde el punto de intersección hasta el círculo es la longitud deseada (PS 4, #31). [Nota: Usando los\(y\) ejes\(x\) y como las líneas de cuerda y las longitudes como se muestra en la imagen, el producto puede ser directamente “leído” 'el\(x\) eje positivo\((\sim(3 / 2)(5 / 2)=15 / 4).]\)