4.3: Teoremas de Ceva y Menelao
- Page ID
- 118027
Cevian (del\(17^{\text {th }}\) siglo matemático italiano Giovanni Ceva (cheh'va)) es una línea de un triángulo desde un vértice hasta un punto (no vértice) de la línea del lado opuesto. Como ejemplos, las medianas de un triángulo, sus bisectores angulares, y sus altitudes son todos cevianos, pero no necesitan ser nada tan especial. Tres de ellos juntos, sin embargo, llevan a un resultado sorprendente y poderoso. El teorema fue probado por Ceva pero también fue probado mucho antes por al-Mu'taman ibn Hüd, un rey de Zaragoza del siglo XI, España.
A este punto solo hemos utilizado medidas positivas pero este teorema utiliza también medidas negativas. No importa qué dirección en una línea llamemos positiva pero, una vez que se toma esa decisión, todas las demás medidas en esa línea son consistentes eso y revertir los puntos finales de un segmento de línea invierte su signo.
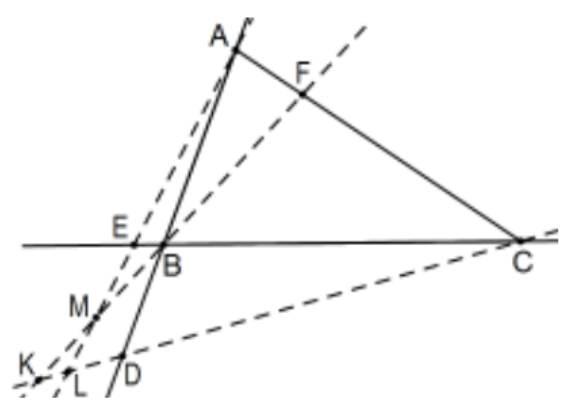
Los cevianos de cada vértice son concurrentes si y solo si el producto de las relaciones firmadas que determinan en cada línea lateral es 1. Es decir, en la figura, los cevianos\(\mathrm{AE}, \mathrm{BF}\), y\(\mathrm{CD}\) son concurrentes si y sólo si\((\mathrm{AD} / \mathrm{DB})(\mathrm{BE} / \mathrm{EC})(\mathrm{CF} / \mathrm{FA})=1\).
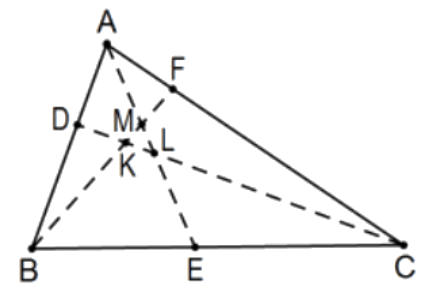
Prueba: Sea o no concurrente los cevianos, considere la línea en A paralela a la línea\(\mathrm{BC}\) y deje\(\mathrm{B}^{\prime}\) ser su intersección con la línea BF y\(\mathrm{C}^{\prime}\) su intersección con CD. Incluso sin intersección común de los cevianos, congruentes ángulos interiores alternos y ángulos verticales verifican cinco pares de triángulos similares;\(\mathrm{D}\) e\(\mathrm{F}\) implican que\(\triangle \mathrm{AC}{ }^{\prime} \mathrm{D} \sim \triangle \mathrm{BCD}\) y\(\triangle \mathrm{AB}^{\prime} \mathrm{F} \sim \triangle \mathrm{CBF}\) y los tres con las intersecciones de cada par de cevianos, AE con BF, AE con CD y BF con CD. Arbitrariamente, tomamos indicaciones en cada línea como positivas si vértice a vértice o vértice a ceviano está aumentando alfabéticamente y\(A\) hacia\(B^{\prime}\) lo largo del resto.
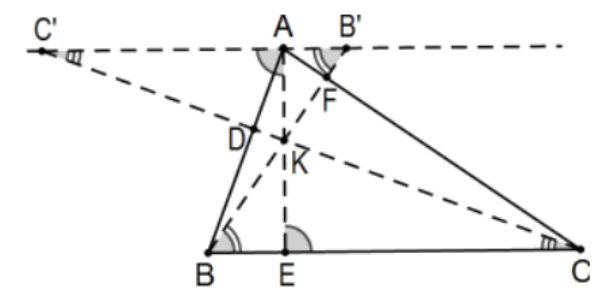
Estos conducen a muchos pares de proporciones iguales que incluyen:
- \(\left(\mathrm{AD} / \mathrm{BD}=-\mathrm{AC}^{\prime} /-\mathrm{BC}\right) \Rightarrow(\mathrm{AD} / \mathrm{DB}=\mathrm{AC} / \mathrm{CB})\)(preocupándose por las medidas firmadas) y
- \(\mathrm{CF} / \mathrm{FA}=\mathrm{CB} / \mathrm{B}^{\prime} \mathrm{A}\)(los signos de las medidas ya están de acuerdo). Supongamos que estos tres cevianos sí se cruzan en un solo punto, digamos\(K\). \(\Delta \mathrm{AC}^{\prime} \mathrm{K} \sim \Delta \mathrm{ECK}\)Entonces\(\triangle \mathrm{AB}{ }^{\prime} \mathrm{K} \sim \triangle \mathrm{EBK}\) y para que:\(\left(\mathrm{AB}^{\prime} / \mathrm{EB}=\mathrm{AK} / \mathrm{EK}=-\mathrm{AC}^{\prime} /-\mathrm{EC}\right) \Rightarrow\left(\mathrm{EB} / \mathrm{AB}^{\prime}=\mathrm{EC} / \mathrm{AC}{ }^{\prime}\right)\) (reciprocas de primero y último) y
- \(\left(\mathrm{EB} / \mathrm{EC}=\mathrm{AB}^{\prime} / \mathrm{AC}^{\prime}\right) \Rightarrow\left(\mathrm{BE} / \mathrm{EC}=\mathrm{B}^{\prime} \mathrm{A} / \mathrm{AC}\right.\)') (vuelve a firmar y también “intercambiando los medios”). Multiplicando ecuaciones\((1),(3)\), y\((2)\), respectivamente, tenemos:
\[(\mathrm{AD} / \mathrm{DB})(\mathrm{BE} / \mathrm{EC})(\mathrm{CF} / \mathrm{FA})=(\mathrm{AC} / \mathrm{CB})\left(\mathrm{B}^{\prime} \mathrm{A} / \mathrm{AC}^{\prime}\right)\left(\mathrm{CB} / \mathrm{B}^{\prime} \mathrm{A}\right)=1 \nonumber\]
Lo contrario es que, si la ecuación se mantiene, entonces\(\mathrm{AE}, \mathrm{BF}, \mathrm{CD}\) son concurrentes. Para probarlo, supongamos que\(\mathrm{K}\) es el punto de intersección de sólo dos de los cevianos,\(B F\) y\(C D\), y deja\(E^{\prime}\) ser la intersección de la línea AK con la línea\(\mathrm{BC}\). Entonces, de la parte del teorema recién probada, (AD/DB)\(\left(\mathrm{BE}^{\prime} / \mathrm{E}^{\prime} \mathrm{C}\right)(\mathrm{CF} / \mathrm{FA})=1\) y, por la hipótesis, tenemos esa (AD/DB) (BE/EC)\((\mathrm{CF} / \mathrm{FA})=1\). El álgebra simple rinde\(\mathrm{BE}^{\prime} / \mathrm{E}^{\prime \prime} \mathrm{C}=\mathrm{BE} / \mathrm{EC}\) y, sumando 1 a cada lado y sumando las fracciones mixtas resultantes, tenemos\(\left(\mathrm{BE}^{\prime}+\mathrm{E}^{\prime} \mathrm{C}\right) / \mathrm{E}^{\prime} \mathrm{C}=(\mathrm{BE}+\mathrm{EC}) / \mathrm{EC}\). Al darse cuenta de que\(\mathrm{E}^{\prime}\) es entre\(\mathrm{B}\)\(\mathrm{C}\) y y así es\(\mathrm{E}\), los numeradores ambos simplifican a BC. Es decir,\(\mathrm{BC} / \mathrm{E}^{\prime} \mathrm{C}=\mathrm{BC} / \mathrm{EC}\). De esto se deduce inmediatamente que\(\mathrm{E}^{\prime} \mathrm{C}=\mathrm{EC}\) y, de su colinealidad y del Postulado Gobernante, E' = E lo que demuestra que los cevianos son concurrentes. QED.
¿Es necesario el detalle “firmado”? ¿Es posible tener el producto de estas proporciones para ser\(-1\)? No sólo la respuesta es “sí”, el resultado es un teorema importante por derecho propio. Hay algunas consecuencias agradables del Teorema de Ceva. Un par de estos ya los hemos visto pero son consecuencias casi triviales de este teorema. Verdaderamente trivial es que las medianas de un triángulo son concurrentes. PS 4, #26 es una prueba no trivial pero también da más información.
Un poco más involucrado es otra prueba de que los bisectores angulares de un triángulo son concurrentes. Esta vez, el teorema de proporcionalidad para bisectores angulares proporciona la respuesta (Ver PS 4, #33). Más complicado, pero indicativo del poder del teorema:
Las altitudes de un triángulo son concurrentes (el punto de intersección se llama ortocentro).
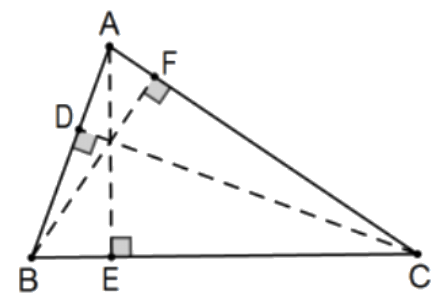
Prueba: Considera aguda\(\triangle \mathrm{ABC}\) y deja que E, F y D sean los pies de las altitudes desde los vértices A, B y C, respectivamente. Por similitud AA:\(\triangle \mathrm{CAD} \sim \triangle \mathrm{BAF}\) (\(\angle \mathrm{A}\)en común)\(\triangle \mathrm{ABE} \sim \triangle \mathrm{CBD}\) (\(\angle \mathrm{B}\)en común)\(\triangle \mathrm{BCF} \sim \triangle \mathrm{ACE}(\angle \mathrm{C}\) en común)
Como antes, asignando signo positivo de\(A\) a\(B, B\) a\(C\), y\(A\) a\(C\):
\([\mathrm{AD} / \mathrm{CA}=\mathrm{AF} / \mathrm{BA}] \Rightarrow[(\mathrm{AD} / \mathrm{CA})(\mathrm{BA} / \mathrm{AF})=1]\)
\([\mathrm{BE} / \mathrm{AB}=-\mathrm{BD} /-\mathrm{CB}] \Rightarrow[(\mathrm{BE} / \mathrm{AB})(\mathrm{CB} / \mathrm{BD})=1]\)
\([\mathrm{CF} / \mathrm{BC}=-\mathrm{CE} /-\mathrm{AC}] \Rightarrow[(\mathrm{CF} / \mathrm{BC})(\mathrm{AC} / \mathrm{CE})=1]\)
Al multiplicar estos tres se obtiene la ecuación:
\ [\ begin {align*} 1 &= [(\ mathrm {AD}/\ mathrm {CA}) (\ mathrm {BA}/\ mathrm {AF})] [(\ mathrm {BE}/\ mathrm {AB}) (\ mathrm {CB}/\ mathrm {BD})] [(\ mathrm {CF}/\ mathrm {BC}) (\ mathrm {BD}) (\ mathrm {BD}) (\ mathrm {BD}) (\ mathrm {BD}) (\ rm {AC}/\ mathrm {CE})]\\ [4pt]
&= [(\ mathrm {AD}\ cdot\ mathrm {BE}\ cdot\ mathrm {CF}) (\ mathrm {BA}\ cdot\ mathrm {CB} \ cdot\ mathrm {AC})/[(\ mathrm {BD}\ cdot\ mathrm {CE}\ cdot\ mathrm {AF}) (\ mathrm {CA}\ cdot\ mathrm {AB}\ cdot\ mathrm {BC})]\\ [4pt]
&= [(\ mathrm {AD}\ cdot\ mathrm {BE}\ cdot\ cdot mathrm {CF}) (\ mathrm {BA}\ cdot\ mathrm {CB}\ cdot\ mathrm {AC})/[(\ mathrm {DB}\ cdot\ mathrm {EC}\ cdot\ mathrm {FA}) (\ mathrm {AC}) (\ mathrm {AC} \ cdot\ mathrm {BA}\ cdot\ mathrm {CB})]\\ [4pt]
&= [(\ mathrm {AD}/\ mathrm {DB}) (\ mathrm {BE}/\ mathrm {EC}) (\ mathrm {CF}/\ mathrm {FA})] [(\ mathrm {BA}/\ mathrm {BA}) (\ mathrm {BA}) (\ mathrm {FA}) (\ mathrm {BA}) (\ mathrm {BA}) (\ rm {CB}/\ mathrm {CB}) (\ mathrm {AC}/\ mathrm {AC})]\\ [4pt]
& =(\ mathrm {AD}/\ mathrm {DB}) (\ mathrm {BE}/\ mathrm { EC}) (\ mathrm {CF}/\ mathrm {FA})\ end {align*}\]
Por el Teorema de Ceva, las líneas AE, BF y CD son concurrentes.
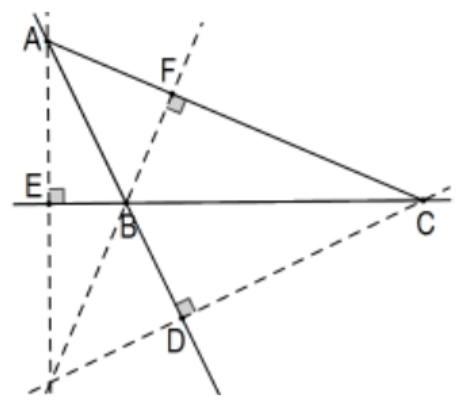
Sin embargo, como lo implica la segunda figura, sí necesitamos extender el resultado a triángulos obtusos. Mirando hacia atrás a los triángulos similares utilizados en el caso agudo, los triángulos indicados siguen siendo similares pero hay un giro, el que usa\(\angle\) B común usa ángulos verticales en lugar del ángulo común. Así los ratios en sí mismos, aún se mantienen y, comprobando, también lo hacen los signos de los ratios. Por ese hecho, la misma prueba de congruencia de las altitudes aún funciona siempre que el Teorema de Ceva también se mantenga para triángulos obtusos. Afortunadamente, lo hace. Si dos de los puntos cevianos están fuera de sus lados correspondientes del triángulo, el Teorema de Ceva aún se mantiene:
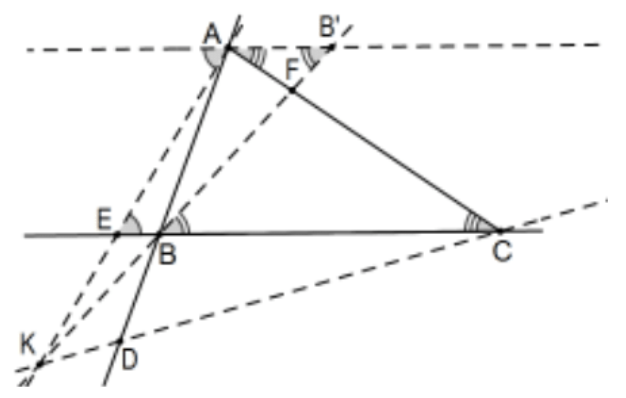
En la figura, D está fuera del segmento\(\mathrm{AB}\) y\(\mathrm{E}\) está fuera del segmento BC. Asumiendo las asignaciones de dirección como antes, esta vez\(\mathrm{DB}\) y\(\mathrm{BE}\) son negativas mientras que todavía\(\mathrm{F}\) está entre\(\mathrm{A}\) y\(\mathrm{C}\) así\(\mathrm{CF}\) es de la misma señal. Entonces, si las líneas se cruzan en un solo punto o no,\((AD/DB)(BE/EC)(CF/FA)\) es positivo. Ese hecho podría simplificar un poco la mecánica de la prueba en el sentido de que podríamos ignorar sus señales y considerar todas las longitudes como positivas, observación que habría significado que no hubiéramos tenido que preocuparnos por dos reversiones a la vez en el caso interno. Procediendo exactamente como antes, considere el paralelo en A a la línea lateral opuesta\(B C\) con\(B^{\prime}\) y\(C^{\prime}\) (\(C^{\prime}\)está fuera de la página a la derecha) como antes y la dirección positiva de\(A\) hacia \(B^{\prime}\)para que, esta vez,\(A C^{\prime}\) sea positivo. Todos los triángulos identificados siguen siendo similares (vértice común en D y en\(\mathrm{K}\) lugar de ángulos verticales) de manera que\(\triangle \mathrm{AC}{ }^{\prime} \mathrm{D} \sim \triangle \mathrm{BCD}\) y\(\triangle \mathrm{AB}{ }^{\prime} \mathrm{F} \sim \triangle \mathrm{CBF}\) y por lo tanto:
- \(\left(\mathrm{AD} / \mathrm{BD}=\mathrm{AC}^{\prime} / \mathrm{BC}\right) \Rightarrow(\mathrm{AD} / \mathrm{DB}=\mathrm{AC} / \mathrm{CB})\)(preocupándose por las medidas firmadas) y
- \(\left(\mathrm{AF} / \mathrm{CF}=\mathrm{AB}^{\prime} / \mathrm{CB}\right) \Rightarrow\left(\mathrm{CF} / \mathrm{FA}=\mathrm{CB} / \mathrm{B}^{\prime} \mathrm{A}\right.\)) (tomar reciprocidades y revertir dos medidas firmadas). Supongamos que estos tres cevianos sí se cruzan en un solo punto, digamos\(K\). \(\Delta \mathrm{AC}{ }^{\prime} \mathrm{K} \sim \Delta \mathrm{ECK}\)Entonces\(\triangle A B^{\prime} K \sim \Delta E B K\) y para que\(\left(\mathrm{AB}^{\prime} / \mathrm{EB}=\mathrm{AK} / \mathrm{EK}=\mathrm{AC}^{\prime} / \mathrm{EC}\right) \Rightarrow\left(\mathrm{EB} / \mathrm{AB}^{\prime}=\mathrm{EC} / \mathrm{AC}^{\prime}\right)\) y
- \(\left(\mathrm{EB} / \mathrm{EC}=\mathrm{AB}^{\prime} / \mathrm{AC}^{\prime}\right) \Rightarrow\left(\mathrm{BE} / \mathrm{EC}=\mathrm{B}^{\prime} \mathrm{A} / \mathrm{AC}{ }^{\prime}\right)\)(“intercambiando medios” y vuelve a firmar). Estas son exactamente las mismas tres ecuaciones que teníamos antes para que, si los cevianos sí se cruzan, entonces el producto de las proporciones es 1. Por el contrario, si asumimos que\(K\) es el punto de intersección de los dos cevianos BF\(\mathrm{CD}\) y y dejamos\(\mathrm{E}^{\prime}\) ser la intersección de línea\(\mathrm{AK}\) con línea\(\mathrm{BC}\), podemos proceder exactamente como antes. QED
Dado que el Teorema de Ceva es relativamente nuevo, resulta algo sorprendente descubrir que el caso de\(-1\) data de la antigüedad con su descubrimiento y primera prueba desconocida. El teorema se llama Teorema de Menelao pero Menelao era una figura de la mitología griega, no uno de los grandes geometros griegos. Al igual que con el teorema de Ceva, hay muchas pruebas de este famoso teorema.
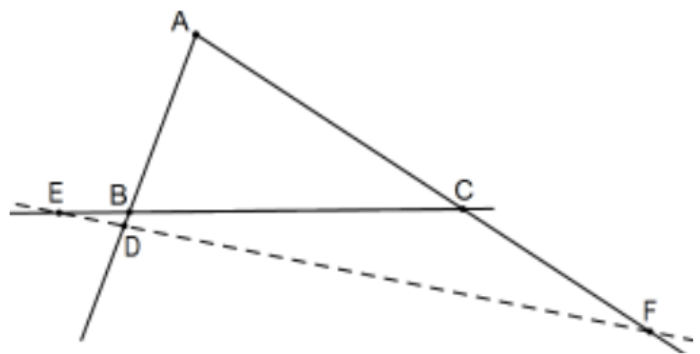
Tres puntos, un punto no vértice de cada línea lateral de un triángulo, son colineales si y solo si el producto de las relaciones firmadas que determinan en las tres líneas laterales es\(-1\). Es decir, en la figura,\(\mathrm{D}, \mathrm{E}\), y\(\mathrm{F}\) son colineales si y sólo si\((\mathrm{AD} / \mathrm{DB})(\mathrm{BE} / \mathrm{EC})(\mathrm{CF} / \mathrm{FA})=-1\).
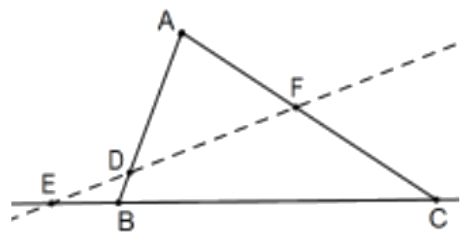
Prueba: Si aún no te has dado cuenta, estas proporciones son positivas si y solo si el punto está dentro del interior de su lado (numerador y denominador positivo o negativo juntos). Además, si uno de estos está en el triángulo mismo, dos deben estarlo. Es decir, si los tres puntos son colineales, la línea que determinan cruza el interior de los lados del triángulo en dos o ningún punto y ambos son posibles como indican las cifras.
Es decir, si los puntos son colineales, o una relación es negativa o los tres son negativos y, en cualquier caso, el producto de ratios es negativo por lo que realmente no necesitamos preocuparnos por medidas firmadas; el producto será negativo.
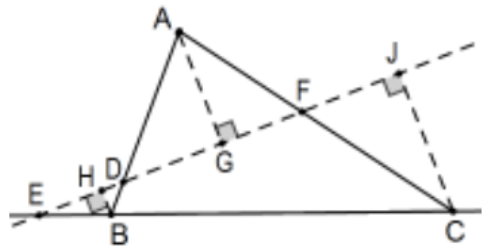
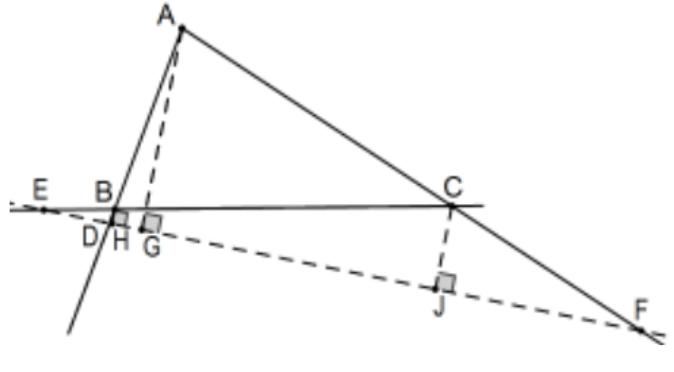
Para iniciar la prueba del caso de dos intersecciones, asumir\(\mathrm{D}, \mathrm{E}\), y\(F\) son colineales y dejar caer la perpendicular de cada vértice. La similitud AA produce varios triángulos similares (E en ángulos comunes y verticales en\(\mathrm{D}\) y\(\mathrm{F}\) en el caso de dos lados y, en el caso del lado cero, ángulos comunes en\(\mathrm{E}\)\(\mathrm{F}\) y ángulos verticales en\(\mathrm{D})\):
\([(\mathrm{AD} / \mathrm{AG}=\mathrm{BD} / \mathrm{BH})] \Rightarrow[(\mathrm{AD} / \mathrm{BD}=\mathrm{AG} / \mathrm{BH})]\)(medios de intercambio)\([(\mathrm{BE} / \mathrm{BH}=\mathrm{CE} / \mathrm{CJ})] \Rightarrow[(\mathrm{BE} / \mathrm{CE}=\mathrm{BH} / \mathrm{CJ})]\) (medios de intercambio)\([(\mathrm{CF} / \mathrm{CJ}=\mathrm{AF} / \mathrm{AG})] \Rightarrow[(\mathrm{CF} / \mathrm{AF}=\mathrm{CJ} / \mathrm{AG})]\) (medios de intercambio) De estos tres tenemos:
\((\mathrm{AD} / \mathrm{DB})(\mathrm{BE} / \mathrm{EC})(\mathrm{CF} / \mathrm{FA})=(\mathrm{AG} / \mathrm{HB})(\mathrm{BH} / \mathrm{JC})(\mathrm{CJ} / \mathrm{GA})\)\(=(\mathrm{AG} / \mathrm{GA})(\mathrm{BH} / \mathrm{HB})(\mathrm{CJ} / \mathrm{JC})=(-1)^{3}=-1\)
y el Teorema de Menelaus se demuestra en una dirección.
Prueba de lo contrario se desprende de este resultado al igual que con Ceva. Es decir, supongamos que este producto es\(-1\) y deja\(\mathrm{E}^{\prime}\) ser la intersección de la línea DF con la línea BC. Por el teorema recién probado, tenemos:
\[(\mathrm{AD} / \mathrm{DB})(\mathrm{BE} / \mathrm{EC})(\mathrm{CF} / \mathrm{FA})=(\mathrm{AD} / \mathrm{DB})\left(\mathrm{BE}^{\prime} / \mathrm{E}^{\prime} \mathrm{C}\right)(\mathrm{CF} / \mathrm{FA}) \nonumber\]
y el hecho que\(\mathrm{E}=\mathrm{E}^{\prime}\) sigue exactamente como antes. QED.


