4.4: Conjunto de problemas 4

A menos que se indique lo contrario, asuma todos los axiomas de geometría neutra (aunque no declarada) y también la forma global del Postulado Paralelo Euclideano.

1. Demostrar que la suma de los ángulos interiores de cualquier triángulo es de dos ángulos rectos$\left(180^{\circ}\right)$.
2. Demostrar que si dos líneas paralelas son cortadas por una transversal, forman ángulos interiores alternados congruentes con la transversal.
3. Demostrar que un cuadrilátero Saccheri o Lambert es un rectángulo.
4. Construir y probar la construcción euclidiana estándar de las tangentes de un punto a un círculo.
5. Demostrar los cuatro casos del Teorema del Ángulo Inscrito. Es decir:

a. El centro del círculo en un rayo.

b. El centro del círculo en el interior del ángulo.

c. El centro del círculo fuera del ángulo.

d. El caso límite; es decir, el caso donde un rayo del ángulo no es una cuerda sino tangente al círculo.

6. Demostrar el teorema del acorde.

7. Demostrar el Caso Tangente del Teorema de la Secante.
8. Supongamos en el boceto que todos los puntos y líneas son como se indica junto con el círculo aparente con su centro en$\mathrm{O}$ y asumir$\mathrm{AB}=9, \mathrm{AF}=8, \mathrm{BC}=6, \mathrm{~GB}=4, \mathrm{GC}=7 / 2$, y$\mathrm{GD}=6$. Encuentra cada uno y (brevemente) explica tu respuesta.

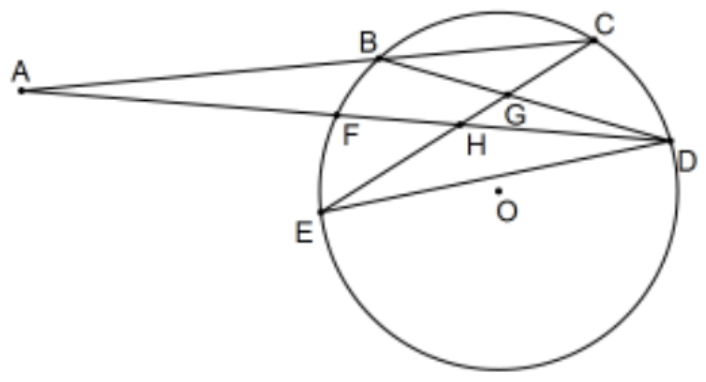
a.$\mathrm{AC}=$

b.$\mathrm{AD}=$

c.$\mathrm{ED}=$

d.$F D=$

e.$E G=$

9. Como #8 pero$m(\angle A)=5^{\circ}, m(\angle E)=30^{\circ}$ asumamos, y$A B \| D E$. Encuentra cada uno y (brevemente) explica por qué. [Nota: ¡NUEVOS DATOS!]

a.$\mathrm{m}(\angle \mathrm{C})=$

b.$\mathrm{m}(\angle \mathrm{CBD})=$

c.$\mathrm{m}(\angle \mathrm{BDA})=$

d.$\mathrm{m}(\angle \mathrm{FDE})=$

e.$\mathrm{m}(\angle \mathrm{BGE})=$

f. probar que los datos de #9 son inconsistentes con los datos de #8.

10. Demostrar que, en geometría hiperbólica, un ángulo inscrito es menor a la mitad de su arco subtendido (ángulo central determinado) si el centro del círculo está sobre o en el interior del ángulo. La prueba falla (puede o no ser cierta) si el centro está fuera del ángulo.

11. Concluimos del Ex 10 que, en geometría hiperbólica, un triángulo inscrito en un semicírculo nunca es un triángulo rectángulo. No olvides confirmar los 3 ángulos.
12. Demostrar que un cuadrilátero es un paralelogramo si sus lados opuestos son congruentes.
13. Demostrar que un cuadrilátero es un paralelogramo si sus ángulos opuestos son congruentes.
14. Demostrar que un cuadrilátero es un paralelogramo si sus diagonales se bisecan entre sí.
15. Demostrar que un cuadrilátero es un paralelogramo si tiene un par de lados opuestos que son paralelos y congruentes.
16. Demostrar que si un segmento de línea une los puntos medios de dos lados de un triángulo, entonces es paralelo a y la mitad de su tercer lado.

[Nota: Aunque es un enfoque mucho más sofisticado, esto es inmediato a partir de una mirada cuidadosa al determinado cuadrilátero asociado.]

17. Dado el segmento de línea unitaria (por ejemplo, el de #18), construya segmentos de las longitudes de todas las soluciones positivas a la ecuación:$x^{2}-2 x-1=0$.

18. Demostrar que las líneas paralelas cortan segmentos proporcionales. [Más explícitamente, las longitudes de los segmentos de 2 transversales a 3 (o más) líneas paralelas son proporcionales (tienen las mismas proporciones)].
19. Demostrar la Prueba algebraica 1 del Teorema de Pitágoras tal como se describe en el texto (hay otros). Si hay conceptos erróneos en cuanto a qué detalles deben probarse, son que la cifra resultante es efectivamente un cuadrado de longitud lateral$\mathrm{a}+\mathrm{b}$, que las cuatro esquinas son triángulos congruentes y que la figura en el medio es de hecho un cuadrado de longitud lateral c. “Obvio” puede ser tentador pero no lo es prueba. Eso sólo funciona para profesores y autores de libros de texto.
20. Demostrar el “triángulo equivalente” Prueba 3 del Teorema de Pitágoras tal como se describe en el texto.
21. Demostrar el “triángulo similar” Prueba 4 del Teorema de Pitágoras tal como se describe en el texto.

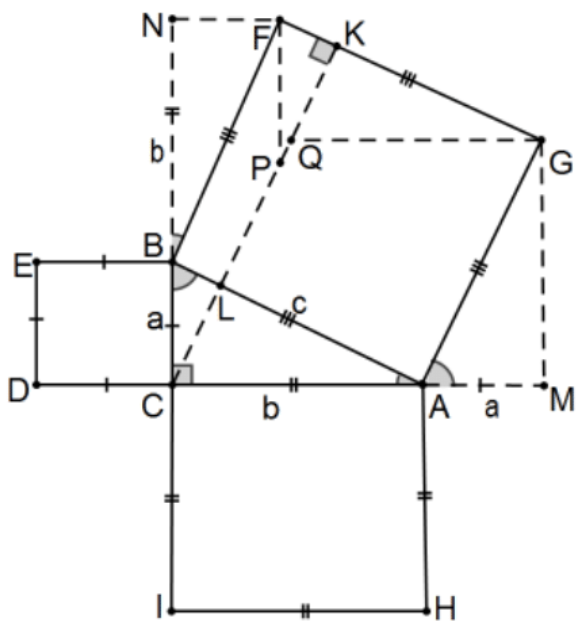
22. Demostrar esta prueba alternativa del Teorema de Pitágoras indicó que evita áreas de triángulos pero en su lugar utiliza los paralelogramos BCPF y ACQG. Explícitamente, extender el rayo CB para determinar$\mathrm{N}$ con BN de longitud$b$ y$M$ a lo largo del rayo CA con AM de longitud$a$ y$K$ es el pie de la$\mathrm{C}$ perpendicular sobre la línea$\mathrm{FG}$. Finalmente, dejar$\mathrm{P}$ y$\mathrm{Q}$ ser determinado por las intersecciones con la línea CK y las líneas paralelas a BC y AC.

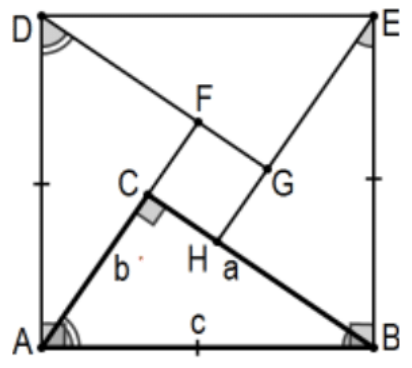
23. Demostrar la prueba algebraica de Bhāshkara (India, b. 1114 d.C.) del Teorema de Pitágoras como se muestra aquí. (“¡He aquí!” fue toda su prueba!) Como es habitual,$\triangle \mathrm{ABC}$ es un triángulo rectángulo con ángulo recto en$\mathrm{C}$ con$a \geq b$. Deje que el segmento AD sea la perpendicular a A de longitud$c$ y, de manera similar, que el segmento$B E$ sea la perpendicular a$B$, también de longitud$c$ para establecer ADEB cuadrilátero. Copiar el original$\angle \mathrm{A}$$\mathrm{D}$ como se indica y el original$\angle \mathrm{B}$ en$\mathrm{E}$ para establecer CFGH cuadrilátero. Demostrar el Teorema de Pitágoras demostrando que ADEB es un cuadrado con área$c^{2}$, CFGH es un cuadrado con área$(a-b)^{2}$, y los cuatro triángulos son todos congruentes con el área$(1 / 2) a b$. Concluir:$c^{2}=a^{2}+b^{2}$. [Nota: ¿Cuál es el grave error lógico en la deliciosa presentación de Khan? https://www.khanacademy.org/, regístrate e ingresa a Bhashkar en “Buscar”.]

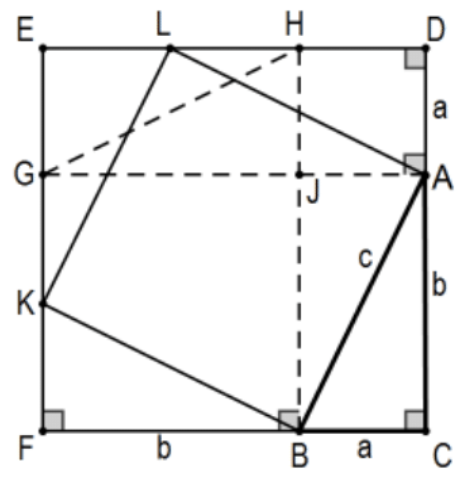
24. Aquí hay otro “¡He aquí!” prueba pero no sé a quién se le ocurrió. Esta vez, comience con el triángulo rectángulo$\triangle \mathrm{ABC}$ y extiéndalo, equivalente a #19, para obtener el cuadrado más grande como lo indican las longitudes y los indicadores perpendiculares. El cuadrado resultante consiste en las 4 esquinas más un cuadrado de longitud lateral c. Emparejando las piezas de esquina y reordenándolas como indican las líneas discontinuas, ¡tenemos la región “sobrante” como un cuadrado de longitud lateral a y otro cuadrado de longitud lateral$b$! Completar los datos de una prueba válida.

25. Considera el siguiente problema: La hipotenusa de un triángulo rectángulo es de 10 pulgadas y la altitud correspondiente del triángulo es de 6 pulgadas. Encuentra el área del triángulo.

i. Explique por qué$\mathrm{A}=(1 / 2) \mathrm{bh}=(1 / 2)(10)(6)=30$ está mal.

ii. Encontrar y verificar el rango de posibles altitudes a una hipotenusa de 10 en un triángulo rectángulo.

26. Demostrar que las medianas de un triángulo son concurrentes y se cruzan en un punto$2 / 3$ de la distancia desde cualquier vértice a su lado opuesto. Este punto se llama el centroide del triángulo y es su centro de gravedad (es decir, se equilibraría en ese punto si fuera una placa de espesor y densidad uniformes).

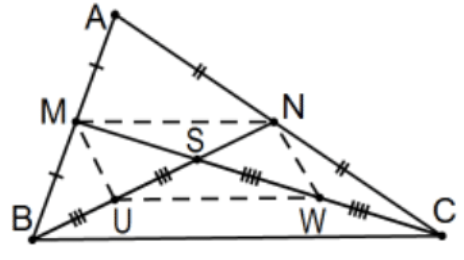
[Pista: Con el boceto dado, use los resultados de los Exs. 14, 15 para demostrar que$S$ es$2 / 3$ del camino de$C$ ida$M$ y vuelta$B$ a$N$. Para probar la concurrencia, dejemos$\mathrm{T}$ ser la intersección de la tercera mediana con una de estas dos y considerar cómo se cruzan a partir de lo que ya se ha probado; es decir, usar eso para probar que$\mathrm{T}=\mathrm{S} .]$

Nota: La intención era una prueba llamada “sintética” (como se indica) pero, en geometría euclidiana, también están disponibles pruebas llamadas “analíticas” para teoremas más avanzados después de que se hayan probado triángulos similares y el Teorema de Pitágoras (necesario para la fórmula de distancia) y asumiendo que los axiomas de geometría euclidiana son “categóricas”. Es decir, probar el teorema en un modelo equivale a probar el teorema en todos los modelos. Aunque cualquier asignación (general) de coordenadas será suficiente, la aritmética algebraica (y por lo tanto, la claridad) se simplifica inmensamente al elegir sabiamente la asignación de coordenadas a los puntos necesarios en la prueba.

27. Dar una prueba analítica del resultado de Ej. $26 .$

[Pista: Una buena manera de comenzar a dejar que un vértice esté en el origen y un lado esté a lo largo del$x$ eje -para que el triángulo general$\triangle \mathrm{ABC}$ tenga coordenadas$A=(0,0), \mathrm{B}=(\mathrm{b}, 0)$, y$\mathrm{C}=(\mathrm{c}, \mathrm{d}) .]$

28. Prueba la Ley del Paralelogramo: En un paralelogramo, la suma de los cuadrados de las diagonales es igual a la suma de los cuadrados de los cuatro lados.

[Nota: La prueba más fácil (no vectorial) que conozco es analítica. Que ABCD sea el paralelogramo. Coordinatizar con el origen en$\mathrm{A}=(0,0), \mathrm{B}=(\mathrm{b}, 0), \mathrm{D}=(\mathrm{c}, \mathrm{d})$ y confirmarlo$\mathrm{C}=(\mathrm{b}+\mathrm{c}, \mathrm{d})$. Ahora calcula la longitud de cada uno de los segmentos involucrados.]

29. Completar la prueba de que dos triángulos de la misma área son equivalentes modificando el teorema correspondiente sobre triángulos de la misma suma de ángulos en geometría hiperbólica.

[Nota: Esta no es la prueba tradicional del hecho que se ha conocido desde la antigüedad sino que es natural a partir de nuestra presentación.]

30. Completar la prueba de que un cuadrilátero tiene un circuncírculo si y sólo si cada par de ángulos opuestos son suplementarios (tiene suma de$180^{\circ}$). [Pista: La figura en el texto es útil. ¿Teorema secante? ¿Teorema de acordes?]

31. Construir el producto de las longitudes de dos segmentos de línea de longitudes dadas comenzando con dos líneas que se cruzan como las líneas de sus acordes eventuales con la suma construida de los segmentos de la intersección de las líneas como uno de los acordes y un segmento de unidad de longitud desde ese punto como uno segmento del otro acorde. Eso determina 3 puntos del círculo deseado y utilizarlos para construir el círculo determinado. La longitud del segmento desde el punto de intersección hasta el círculo es la longitud deseada. Utilizar el Teorema de Acorde para probar que la construcción es válida. Finalmente, hacer los ajustes apropiados para construir el cociente de las longitudes (la prueba es esencialmente la misma).

32. Griego Diámetro de la Tierra Los antiguos griegos no sólo sabían que la tierra era una esfera, sabían su tamaño con una precisión razonable. En$240 \mathrm{BC}$, Eratóstenes estimó el diámetro de la tierra midiendo el ángulo formado en la parte superior de un polo vertical que subtendía su sombra en un punto a una distancia conocida directamente al norte de otro punto cuando el sol estaba directamente sobre el primer punto donde un polo no tendría visible sombra (usó el sol brillando en el fondo de un pozo). Hay un par de enfoques que utilizan esta idea para aproximar la circunferencia (equivalentemente, el diámetro o radio) de la tierra y ambos comienzan con la misma configuración descrita de la siguiente manera.

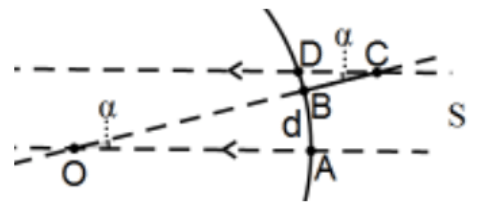
Solo se necesita el punto norte si se encuentra a una distancia conocida directamente al norte del gran círculo determinada por un punto con sol directamente sobre la cabeza a una hora determinada en un día determinado. Supongamos que la figura adjunta es la sección transversal de la tierra determinada por el plano de$\mathrm{O}, \mathrm{S}$ y$\mathrm{B}$; respectivamente, el centro de la tierra, el centro del sol (demasiado lejos a la derecha para ser visible), y un punto a una distancia conocida$\mathrm{d}$ directamente al norte del punto A en el que el sol está directamente sobre la cabeza (por simplicidad, en el ecuador, al mediodía en un equinoccio). Ambas ideas asumen que el sol está tan lejos que podemos considerar que los rayos del sol son paralelos en lugar de irradiar desde la fuente puntual$S$. Piense en la línea$S O=A O$ como un rayo de luz del sol y la otra línea es el rayo paralelo a través$C$, la parte superior de un poste vertical erigido en$B$. Que D sea el punto donde ese rayo golpea la tierra. Dado que la línea OC es una transversal a dos líneas paralelas,$\angle \mathrm{AOB} \cong \angle \mathrm{BCD}$ debido a que son ángulos interiores alternados formados por un transversal a líneas paralelas y dejar$\alpha=\mathrm{m}(\angle \mathrm{AOB})=\mathrm{m}(\angle \mathrm{BCD})$.

32a. Eratóstenes utilizó la simple observación de que la medida del ángulo central$\alpha^{\circ}$ comparada con el círculo completo$360^{\circ}$ es proporcional a la longitud del arco$\mathrm{d}$ en comparación con la circunferencia de la Tierra (el círculo) c. Simbólicamente, tenemos$\alpha / 360=\mathrm{d} / \mathrm{c}$ así eso$\mathrm{c}=360 \mathrm{~d} / \alpha$. Siguiendo a Eratóstenes, aproximar la circunferencia de la tierra para$\mathrm{d} \sim 575 \mathrm{mi}$ y$\alpha \sim 7.2^{\circ}$ (es difícil medir el ángulo con$\alpha$ tanta precisión).

32b. Asumiendo que el punto no$B$ está muy lejos de$A$ (relativamente pequeño$\alpha$), es razonable considerar que la tierra es plana (¡ciertamente se siente plana!) y reemplazamos el arco AD por la perpendicular común a las dos líneas paralelas a través del punto B produciendo los puntos A', D', y, con el radio de la Tierra$r$, dos similares,$\mathrm{r} / \mathrm{BA}^{\prime}=\mathrm{BC} / \mathrm{BD}^{\prime}$ de los cuales tenemos la obvia aproximación:$\mathrm{r} / \mathrm{m}(\operatorname{arc}(\mathrm{BA})) \sim \mathrm{BC} / \mathrm{m}(\operatorname{arc}(\mathrm{BD})$ y finalmente:

$\mathrm{r} \sim(\mathrm{m}(\operatorname{arc}(\mathrm{BA})))\left(\mathrm{BC} / \mathrm{m}\left(\operatorname{arc}\left(\mathrm{BD}^{\prime}\right)\right)\right)$con todo a la derecha fácilmente medido (fácil de medir$\mathrm{m}(\operatorname{arc}(\mathrm{BD} \mathrm{m}(\operatorname{arc}(\mathrm{BD}) \sim 11 / 2 \mathrm{ft}$ para la longitud del poste$\mathrm{BC}=10 \mathrm{ft}$. Esbozar la situación y aproximar el radio de la tierra$r$ y su circunferencia C.

33. Usa el Teorema de Ceva para demostrar que las medianas de un triángulo son concurrentes. [Pista: ¡Absolutamente trivial!]

34. Usa el Teorema de Ceva para demostrar que los bisectores angulares de un triángulo son concurrentes. [Pista: Usa el teorema de que un ángulo bisectriz de un triángulo divide el lado opuesto proporcionalmente con los lados del ángulo.]
35. En geometría euclidiana, dos polígonos son iguales en área si y sólo si son equivalentes. [La prueba formal es por inducción en$n$, los lados numéricos en el polígono, como equivalente a algún triángulo, así entonces el caso del triángulo completa la solución. Es decir, para dos polígonos de número de lados m y$n$ de la misma área, reducirlos ambos a triángulos de una misma área, usar el hecho de que estos dos son equivalentes y luego, por simetría y transitividad, concluyen que los polígonos originales son equivalentes. En lugar de probar esto formalmente, explique la reducción de este hexágono ABCDEF al triángulo FHJ, reemplazando uno por uno un vértice con un borde mientras se mantiene la misma área debido a la equivalencia (es decir, “cortar” y mover triángulos congruentes).]

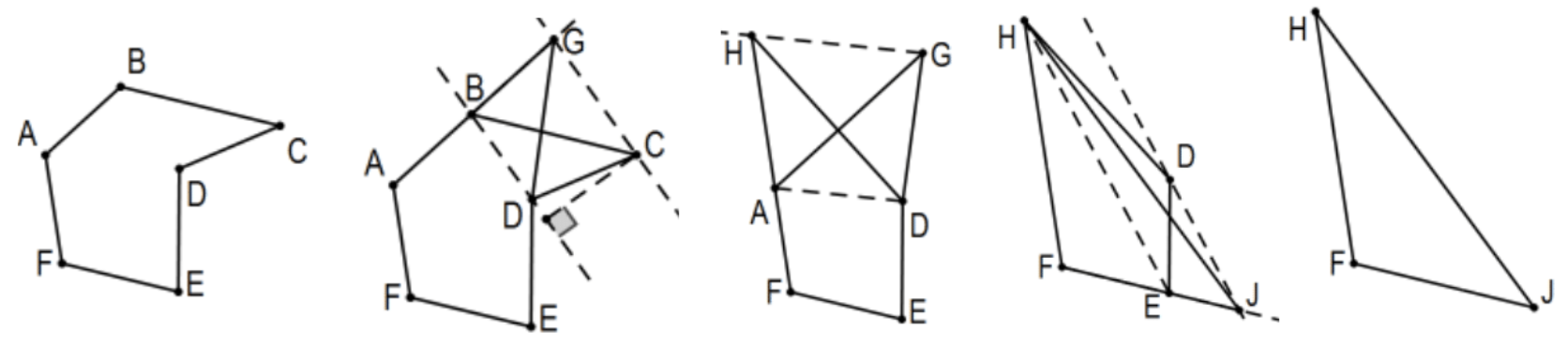
Aunque la suma de ángulos reemplaza área por triángulos en el teorema correspondiente en geometría hiperbólica, la generalización natural a polígonos no es cierta. La idea parece que podría funcionar “cortando” un triángulo para reducir el número de vértices mediante el uso de la línea de puntos medios y cuadriláteros Saccheri. Es decir, en el primer paso anterior, en lugar del paralelo en C a la línea BD (eso no es único), comenzar con la intersección de línea$A B$ y la línea de puntos medios de segmentos$B C$ y$D C$ y duplicar el segmento desde$B$ hasta el punto de intersección para establecer punto$\mathrm{G}$ eliminando así el vértice B. En el caso euclidiano, ese enfoque determina exactamente el mismo punto G. Eliminar un vértice con un polígono equivalente reduce la suma del ángulo exactamente$180^{\circ}$, la importancia de la construcción. ¿Problema? Puede que no haya$180^{\circ}$ “de sobra”. Para ver por qué esto es así, considera el cuadrilátero regular ABCD que se muestra en este modelo de Poincaré, la suma del ángulo es mucho menor que$180^{\circ}$ (cada ángulo es menor que$45^{\circ}$) por lo que no se puede eliminar ningún vértice para obtener un triángulo equivalente porque tendría que tener suma de ángulo exactamente$180^{\circ}$ menos pero esto es imposible.

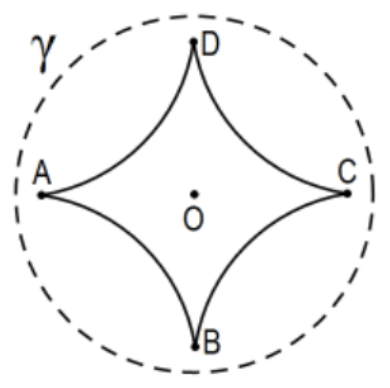
36. ¿Qué pasa con la prueba euclidiana en la situación hiperbólica?