4.2: Prueba de Geometría Analítica
- Page ID
- 118028
Hemos estado haciendo lo que se conoce como prueba “sintética”, probando teoremas directamente desde los axiomas enteramente en abstracto (a pesar del enfoque un tanto poco ortodoxo de reconocer que nunca declaramos formalmente estos axiomas en lugar de lo habitual, mintiendo al respecto). Las imágenes que dibujamos son útiles pero sin sentido a menos que aceptemos el plano idealizado de una pizarra u hoja de papel (y puntos asociados, líneas y similares) como modelo para la geometría abstracta que pretende ser estrictamente conceptual. Otro modelo que nos han entrenado para creer es exactamente lo mismo es el plano cartesiano. De hecho, se trata de un modelo completamente separado que no tiene nada en común con nuestro plano habitual salvo nuestra convicción de que son uno y lo mismo. De hecho, son muy diferentes. En otro sentido, sin embargo, son los mismos; esa es la naturaleza de los axiomas para que la geometría euclidiana sea “categórica” introducida en la Introducción. La idea es que una prueba en un modelo de geometría euclidiana pueda identificarse completamente (lo que son puntos, líneas, etc.) en cualquier otro modelo o en la situación abstracta “libre de modelos” y la prueba será igualmente válida. Es decir, una prueba de avión cartesiano realmente es una prueba válida. Aunque parte de la geometría completa (especialmente en el espacio euclidiano n-dimensional) se maneja mejor con notación vectorial (congruencia angular por ejemplo), estamos tratando de presentar la situación en el nivel más bajo posible para la comprensión más básica.
Recordemos que al introducir el modelo de disco de Poincaré para geometría hiperbólica, comenzamos con el modelo siendo un triple,\(\mathcal{L}=(\theta, L, C)\), para el conjunto de puntos de la geometría, los subconjuntos que se llamarían líneas, y los subconjuntos a llamarse círculos. Estábamos “fudging” un poco en que el concepto de longitud de segmento (distancia entre 2 puntos necesarios para probar el Postulado Gobernante) significaba que los “círculos” ya tenían una definición como conjunto de todos los puntos equidistantes de algún punto llamado su centro. El problema era que no habíamos desarrollado mucho sentimiento por la distancia Poincaré (todavía no lo han hecho, ¡la verdad sea dicha!). En esta “nueva” situación, la distancia euclidiana no es un problema, la fórmula tradicional de distancia, entonces\(l=(0, L)\) donde:
\(p=\left\{(\mathrm{x}, \mathrm{y}) \mid \mathrm{x}, \mathrm{y}\right.\)el conjunto de todos los pares ordenados,\(\left.\mathbf{R} \times \mathbf{R}=\mathbf{R}^{2}\right\}\)
\(\mathcal{L}=\left\{\ell \mid l=\{(x, y) \mid a x+b y=c\}\right.\)para algunos\(\left.a, b, c \in \mathbf{R}, a^{2}+b^{2}>0\right\}\) (es decir, no ambos\(a=0\) y\(\left.b=0\right)\).
Es decir, una línea es solo el conjunto de todas las soluciones a cualquier “ecuación lineal” (¡incluso las palabras que usamos están inclinando la mesa de pinball!). En esta configuración de producto cartesiano, estamos tan acostumbrados a identificar cada par ordenado como un punto único en el plano de coordenadas que tenemos que obligarnos a pensar que no es más que un paréntesis izquierdo “(” seguido de dos números reales separados por una coma y un paréntesis derecho. Incluso el espacio euclidiano 3 hace que la identificación sea obvia, aunque más difícil de esbozar. Para tener una mejor idea, piense en un punto\(\mathbf{R}^{\mathrm{n}}\) por dentro\(\mathrm{n} \geq 4\) y vea si la identificación sigue siendo tan clara. Para confirmar que se trata de un modelo para geometría plana euclidiana cuando\(n=2\), tendríamos que probar todos los axiomas como teoremas pero, de hecho, algunos de ellos los hemos estado haciendo desde Álgebra 1! Por ejemplo, la prueba del Axioma 1 no es más que encontrar la ecuación (siendo más cuidadosos, “an”) que es satisfecha por dos pares dados de pares ordenados y confirmar que cualquier ecuación lineal que sea satisfecha por estos dos pares tiene exactamente el mismo conjunto de soluciones (mismo conjunto de soluciones). Eso es sólo un problema estándar de Álgebra I si se hace en términos de coeficientes generales\(\mathrm{P}_{1}\left(\mathrm{x}_{1}, \mathrm{y}_{1}\right) \neq \mathrm{P}_{2}\left(\mathrm{x}_{2}, \mathrm{y}_{2}\right)\) tomando en cuenta los casos especiales de\(\mathrm{x}_{1}=\mathrm{x}_{2}\) exclusividad o\(\mathrm{y}_{1}=\mathrm{y}_{2}\). Sin embargo, considerar este modelo para la geometría euclidiana de una manera tan formal frustraría el propósito. La idea es utilizar nuestra estrecha identificación del plano cartesiano (ejes de coordenadas en el plano convencional) para dar una prueba alternativa, a veces más simple.
La distancia entre dos puntos es solo la fórmula de distancia basada en el teorema de Pitágoras. Los ángulos son un poco más complicados pero generalmente no aparecen en los tipos de pruebas que se construyen fácilmente “analíticamente”. Para líneas que no son ni paralelas al\(\mathrm{x}\) eje -eje ni al\(\mathrm{y}\) eje -eje, es fácil probar que líneas distintas son paralelas (no hay puntos en común) si y solo si tienen la misma pendiente siempre y cuando nos extendamos paralelas para incluir la idea de propiedad de equivalencia “reflexividad” que una línea se defina para que sea paralela a sí misma. De igual manera, es fácil demostrar que las líneas son perpendiculares si y sólo si sus pendientes son recíprocas negativas entre sí (producto es -1) junto con el caso especial de paralelos a los ejes de coordenadas. Nota: Esta no es una definición perpendicular ya tiene significado definido - esto es un teorema. La medida de los ángulos se realiza más fácilmente con notación vectorial. No lo necesitaremos sino por el bien de la integridad:
La medida del ángulo entre dos vectores\(u\) y\(v\) en el origen es\(\alpha=\cos ^{-1}(u \cdot v /\|u\|\|V\|)\), el tamaño de un ángulo siendo el coseno el producto de punto de los vectores dividido por el producto de sus longitudes así que para general\(\angle \mathrm{BAC}\) con \(\mathrm{B}\left(\mathrm{x}_{\mathrm{B}}, \mathrm{y}_{\mathrm{B}}\right), \mathrm{A}\left(\mathrm{x}_{\mathrm{A}}, \mathrm{y}_{\mathrm{A}}\right)\), y\(C\left(\mathrm{x}_{\mathrm{C}}, \mathrm{y}_{\mathrm{C}}\right)\):
\[m(\angle B A C)=\cos ^{-1}\left(\frac{\left(x_{B}-x_{A}\right)\left(x_{C}-x_{A}\right)+\left(y_{B}-x_{A}\right)\left(y_{C}-x_{A}\right)}{\left(\sqrt{\left(x_{B}-x_{A}\right)^{2}+\left(y_{B}-x_{A}\right)^{2}}\right)\left(\sqrt{\left(x_{C}-x_{A}\right)^{2}+\left(y_{C}-x_{A}\right)^{2}}\right)}\right) \nonumber \]
Esto se expresó en términos del plano\(\left(\mathbf{R}^{n}\right.\) donde\(\left.n=2\right)\) pero el mismo enfoque vectorial es válido para cualquiera\(n\). Es decir, la misma fórmula vectorial para la medida de un ángulo\(\mathbf{R}^{\mathrm{n}}\) para cualquier\(\mathrm{n}\).
En lugar de más de los detalles, aquí hay un ejemplo de un teorema probado sintéticamente ahora usando una prueba analítica. Ejemplos de otros teoremas se dan en PS 4, #27 y #28.
La línea determinada por los puntos medios de dos lados de un triángulo es paralela al tercer lado y la longitud de su segmento es la mitad de ese tercer lado.
Prueba: Para minimizar la complejidad algebraica, es muy útil coordinar el plano de tal manera que la aritmética algebraica sea lo más fácil posible teniendo cuidado, por supuesto, de ser completamente general en la asignación. Una simplificación común es con un lado de una figura que se estudia a lo largo del\(x\) eje y un punto importante\((0,0)\). En este caso, un lugar razonable para comenzar sería que nuestro triángulo general estuviera\(\triangle \mathrm{ABC}\) con vértices de par ordenados\(\mathrm{A}(0,0), \mathrm{B}(\mathrm{a}, \mathrm{b})\), y\(\mathrm{C}(\mathrm{c}, 0)\) con\(\mathrm{b} \neq 0\) y\(\mathrm{c} \neq 0\) como se muestra en la imagen. [Aún más fácil hubiera sido\(\mathrm{A}(\mathrm{a}, 0), \mathrm{B}(0, \mathrm{~b})\), y\(\mathrm{C}(\mathrm{c}, 0)\) con\(\mathrm{b} \neq 0\) y\(\mathrm{a} \neq \mathrm{c}\).] Por supuesto, esto supone que el cálculo del punto medio de un segmento es conocido pero escribir una ecuación para la línea MN\((\mathrm{y}=\mathrm{b} / 2)\) para confirmar que es paralela al\(\mathrm{x}\) eje\((\mathrm{y}=0)\) -es una trivialidad como lo es calcular la longitud del segmento\(M N\) y confirmando que es la mitad de la longitud del segmento AC. QED.
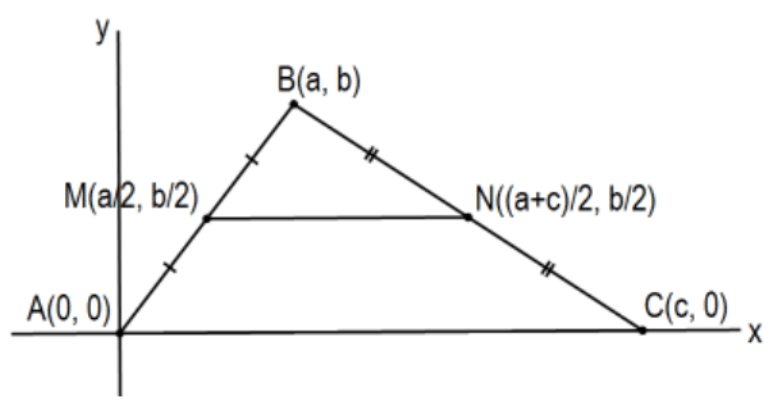
Nota: Esto es tan sencillo que casi parece que estamos engañando pero es una prueba perfectamente válida asumiendo el hecho de que los axiomas para la geometría euclidiana son categóricos y que este es un modelo para la geometría euclidiana.