1.3: Clasificaciones de ángulo
- Page ID
- 114554
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
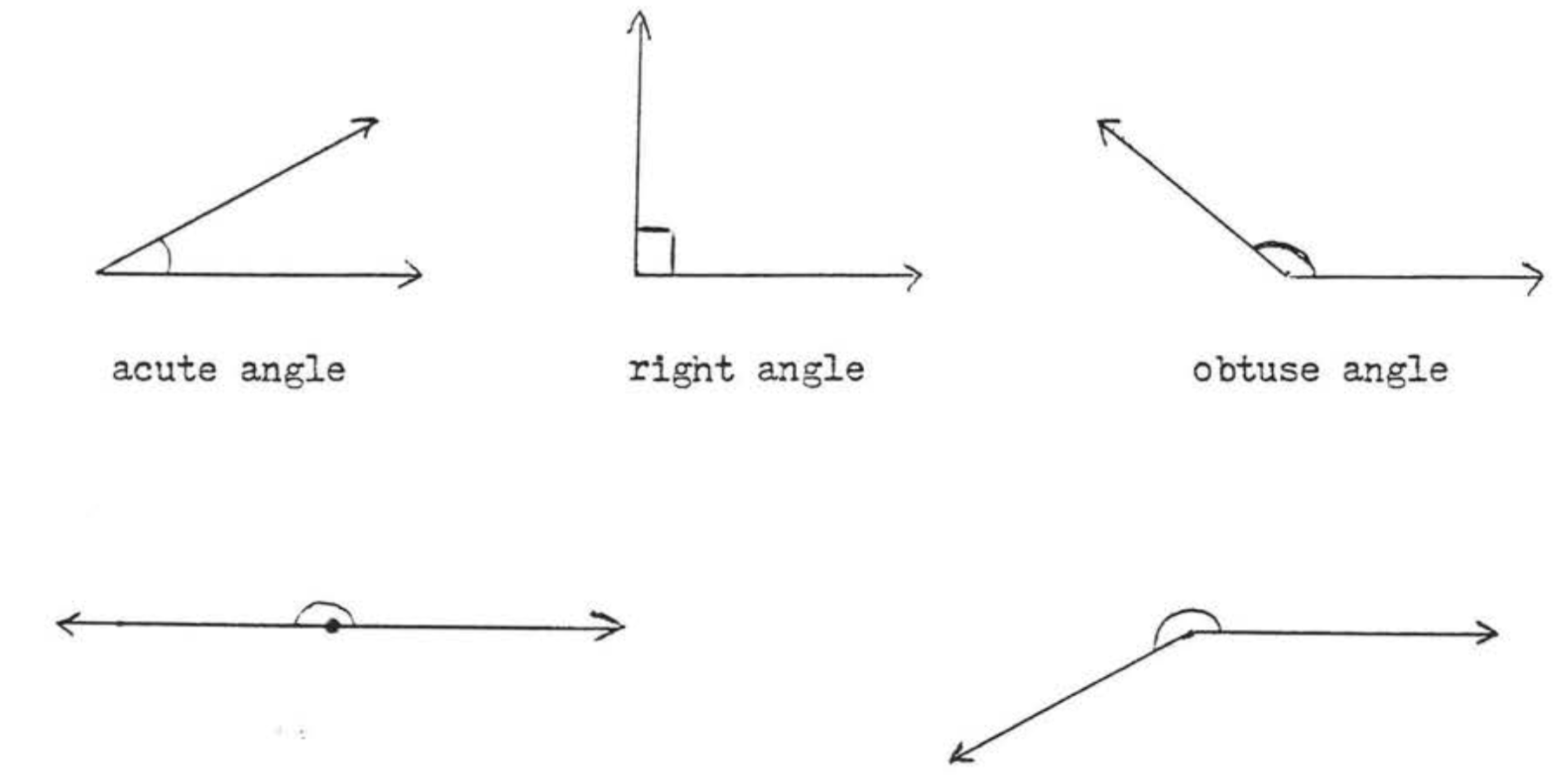
Los ángulos se clasifican de acuerdo a sus medidas de la siguiente manera:
- Un ángulo agudo es un ángulo cuya medida es entre\(0^{\circ}\) y\(90^{\circ}\).
- Un ángulo recto es un ángulo cuya medida es\(90^{\circ}\). A menudo usamos un pequeño cuadrado para indicar un ángulo recto.
- Un ángulo obtuso es un ángulo cuya medida es entre\(90^{\circ}\) y\(180^{\circ}\).
- Un ángulo recto es un ángulo cuya medida es\(180^{\circ}\). Un ángulo recto es solo una línea recta con uno de sus puntos designado como vértice.
- Un ángulo reflejo es un ángulo cuya medida es mayor que\(180^{\circ}\).
Observe que un ángulo se puede medir de dos maneras. En la Figura\(\PageIndex{2}\),\(\angle ABC\) es un reflejo de\(240^{\circ}\) o un ángulo obtuso de\(120^{\circ}\) dependiendo de cómo se mide. A menos que se indique lo contrario, siempre asumiremos que el ángulo tiene una medida menor que\(180^{\circ}\).

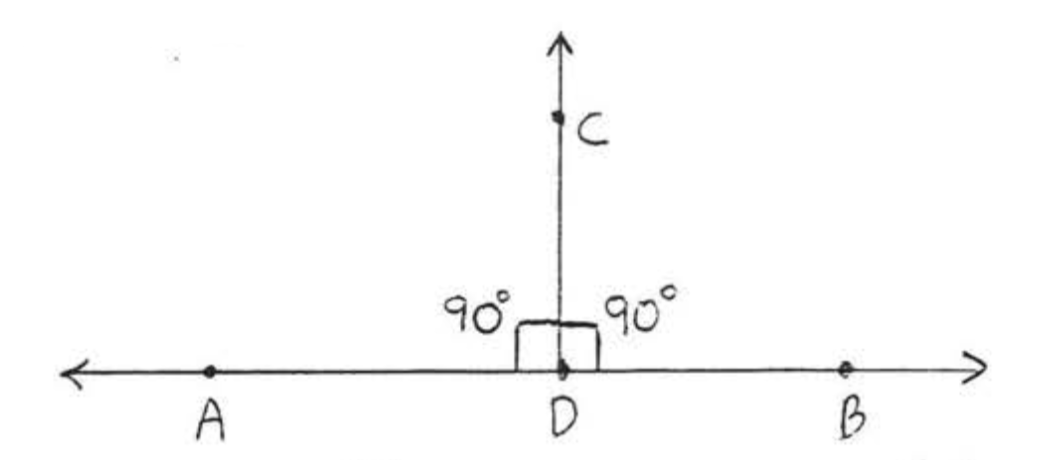
Las líneas son perpendiculares si se encuentran para formar ángulos rectos. En la Figura\(\PageIndex{3}\),\(\overleftrightarrow{AB}\) es perpendicular a\(\overleftrightarrow{CD}\). El símbolo para perpendicular es\(\perp\) y escribimos\(\overleftrightarrow{AB} \perp \overleftrightarrow{CD}\).
La bisectriz perpendicular de un segmento de línea es una línea perpendicular al segmento de línea en su punto medio, En la Figura\(\PageIndex{4}\),\(\overleftrightarrow{CD}\) es una bisectriz perpendicular de\(AB\).

Dos ángulos se llaman complementarios si la suma de sus medidas es\(90^{\circ}\). Cada ángulo se llama el complemento del otro. Por ejemplo, los ángulos de\(60^{\circ}\) y\(30^{\circ}\) son complementarios.

Encuentra el complemento de un\(40^{\circ}\) ángulo.
Solución
\(90^{\circ} - 40^{\circ} = 50^{\circ}\).
Respuesta:\(50^{\circ}\).
Encontrar\(x\) y los ángulos complementarios:

Solución
Dado que\(\angle BAD = 90^{\circ}\),
\[\begin{array} {rcl} {x^2 + x} & {90^{\circ}} \\ {x^2 + x - 90} & {0} \\ {(x - 9)(x + 10)} & {0} \end{array}\]
\[\begin{array} {rcl} {x - 9} & = & {0} \\ {x} & = & {9} \end{array}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \begin{array} {rcl} {x + 10} & = & {0} \\ {x} & = & {-10} \end{array}\]
\(\angle CAD = x = 90^{\circ}\). \(\angle CAD = x = -10^{\circ}.\)
\(\angle BAC = x^2 = 9^2 = 81^{\circ}\).
\(\angle BAC = \angle CAD = 81^{\circ} + 9^{\circ} = 90^{\circ}\).
Rechazamos la respuesta\(x = -10\) porque la medida de un ángulo siempre es positiva. (En trigonometría, cuando se introducen ángulos dirigidos, los ángulos pueden tener medida negativa. En este libro, sin embargo, se pensará que todos los ángulos tienen una medida positiva,)
Comprobar,\(x = 9\):

Respuesta:\(x = 9\),\(\angle CAD = 9^{\circ}\),\(\angle BAC = 81^{\circ}\).
Dos ángulos se llaman suplementarios si la suma de sus medidas es\(180^{\circ}\). Cada ángulo se llama el suplemento del otro. Por ejemplo, ángulo de\(150^{\circ}\) y\(30^{\circ}\) son suplementarios.

Encuentra el suplemento de un ángulo de\(40^{\circ}\).
Solución
\(180^{\circ} - 40^{\circ} = 140^{\circ}\).
Respuesta:\(140^{\circ}\).
Encuentra\(x\) y los ángulos suplementarios:

Solución
Dado que\(\angle ADB = 180^{\circ}\),
\[\begin{array} {rcl} {4x - 20 + x} & = & {180^{\circ}} \\ {5x} & = & {180 + 20} \\ {5x} & = & {200} \\ {x} & = & {40} \end{array}\]
\(\angle ADC = 4x - 20 = 4(40) - 20 = 160 - 20 = 140^{\circ}\)
\(\angle BDC = x = 40^{\circ}\),
\(\angle ADC + \angle BDC = 140^{\circ} + 40^{\circ} = 180^{\circ}\).
Comprobar:

Responder
\(x = 40, \angle ADC = 140^{\circ}, \angle BDC = 40^{\circ}\).
Encuentra\(x, y, z\):

Solución
\(x^{\circ} = 180^{\circ} - 80^{\circ} = 100^{\circ}\)porque\(x^{\circ}\) y\(80^{\circ}\) son las medidas de ángulos suplementarios.
\[\begin{array} {l} {y^{\circ} = 180^{\circ} - x^{\circ} = 180^{\circ} - 100^{\circ} = 80^{\circ}.} \\ {z^{\circ} = 180^{\circ} - 80^{\circ} = 100^{\circ}.} \end{array}\]
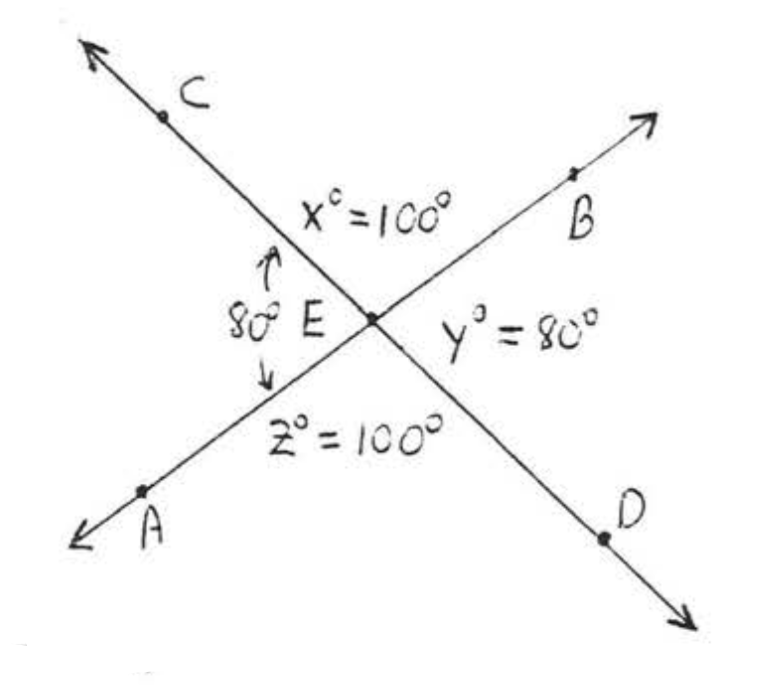
Respuesta:\(x = 100\),\(y = 80\),\(z = 100\).
Cuando dos líneas se cruzan como en el EJEMPLO E, forman dos pares de ángulos que son opuestos entre sí llamados ángulos verticales, En la Figura\(\PageIndex{7}\),\(\angle x\) y\(\angle x'\) son un par de ángulos verticales. \(\angle y\)y\(\angle y'\) a.re el otro par de ángulos verticales, Como sugiere el Ejemplo\(\PageIndex{5}\), \(\angle x = \angle x'\) and \(\angle y = \angle y'\). To see this in general, we can reason as follows: \(\angle x\) is the supplement of \(\angle y\) so \(\angle x = 180^{\circ} - \angle y\). \(\angle x'\) is also the supplement of \(\angle y\) so \(\angle x' = 180 - \angle y\). Therefore \(\angle x = \angle x'\). Similarly, we can show \(\angle y = \angle y'\). Therefore vertical angles are always equal.

Ahora podemos usar “los ángulos verticales son iguales” para resolver problemas:
Buscar\(x, y\), y\(z\):

Solución
\(\angle x = 180^{\circ} - 80^{\circ} = 100^{\circ}\)porque\(\angle x\) es el suplemento de\(80^{\circ}\).
\(\angle y = 80^{\circ}\)porque los ángulos verticales son iguales.
\(\angle z = \angle x = 100^{\circ}\)porque los ángulos verticales son iguales.
Respuesta:\(x = 100\),\(y = 80\),\(z = 100\).
Encuentra\(x\):

Solución
Dado que los ángulos verticales son iguales,\(10x^2 = 40^{\circ}\).
\(\begin{array} {rclcrcl} {\text{Method 1:} \ \ \ \ \ \ 10x^2} & = & {40} & \ \ \ \ \ \ \ \ \ & {\text{Method 2:} \ \ \ \ \ \ 10x^2} & = & {40} \\ {10x^2 - 40} & = & {0} & \ \ \ \ \ \ \ \ \ & {\dfrac{10x^2}{10}} & = & {\dfrac{40}{10}} \\ {(10)(x^2 - 4)} & = & {0} & \ \ \ \ \ \ \ \ \ & {x^2} & = & {4} \\ {x^2 - 4} & = & {0} & \ \ \ \ \ \ \ \ \ & {x} & = & {\pm 2} \\ {(x + 2)(x - 2)} & = & {0} & \ \ \ \ \ \ \ \ \ & {} & & {} \end{array}\)
\(\begin{array} {rcl} {x + 2} & = & {0} \\ {x} & = & {-2} \end{array}\)\(\begin{array} {rcl} {x - 2} & = & {0} \\ {x} & = & {2} \end{array}\)
Si\(x = 2\) entonces\(\angle AEC = 10x^2 = 10(2)^2 = 10(4) = 40^{\circ}\).
Si\(x = -2\) entonces\(\angle AEC = 10x^2 = 10(-2)^2 = 10(4) = 40^{\circ}\).
Aceptamos la solución\(x =-2\) aunque\(x\) sea negativa porque el valor del ángulo\(10x^2\) sigue siendo positivo.
Comprobar:

Respuesta:\(x = 2\) o\(x = -2\).
En el diagrama,\(AB\) representa un espejo,\(CD\) representa un rayo de luz que se aproxima al espejo desde\(C\), y\(E\) representa el ojo de una persona que observa el rayo tal como se refleja desde el espejo en\(D\). De acuerdo con una ley de la física\(\angle CDA\),, llamada el ángulo de incidencia, es igual\(\angle EDB\), llamado el ángulo de reflexión. Si\(\angle CDE = 60^{\circ}\), ¿cuánto es el ángulo de incidencia?

Solución
Vamos\(\x^{\circ} = \angle CDA = \angle EDB\).
\[\begin{array} {rcl} {x + x + 60} & = & {180} \\ {2x + 60} & = & {180} \\ {2x} & = & {120} \\ {x} & = & {60} \end{array}\]
Respuesta:\(60^{\circ}\)
La afirmación “los ángulos verticales son siempre iguales” es un ejemplo de un teorema. Un teorema es una afirmación que podemos demostrar que es cierta, Una prueba es un proceso de razonamiento que utiliza declaraciones ya conocidas como verdaderas para mostrar la verdad de una nueva afirmación, Un ejemplo de una prueba es la discusión que precede a la afirmación “los ángulos verticales son siempre iguales”. Utilizamos hechos sobre ángulos suplementarios que ya se conocían para establecer la nueva afirmación, que “los ángulos verticales son siempre iguales”.
Idealmente nos gustaría probar todas las afirmaciones en matemáticas que creemos que son ciertas. Sin embargo antes de que podamos comenzar a probar algo necesitamos algunas afirmaciones verdaderas con las que comenzar. Tales afirmaciones deben ser tan evidentes como para no requerir pruebas por sí mismas, Una declaración de este tipo, que suponemos que es verdadera sin pruebas, se llama postulado o axioma. Un ejemplo de un postulado es la suposición de que todos los ángulos se pueden medir en grados. Esto se utilizó sin que en realidad se dijera en nuestra prueba que “los ángulos verticales son siempre iguales”,
Teoremas, pruebas y postulados constituyen el corazón de las matemáticas y nos encontraremos con muchos más de ellos a medida que continuemos nuestro estudio de la geometría.
Problemas
1. Encuentra el complemento de un ángulo de
- \(37^{\circ}\)
- \(45^{\circ}\)
- \(53^{\circ}\)
- \(60^{\circ}\)
2. Encuentra el complemento de un ángulo de
- \(30^{\circ}\)
- \(40^{\circ}\)
- \(50^{\circ}\)
- \(81^{\circ}\)
3 - 6. Encontrar\(x\) y los ángulos complementarios:
3. 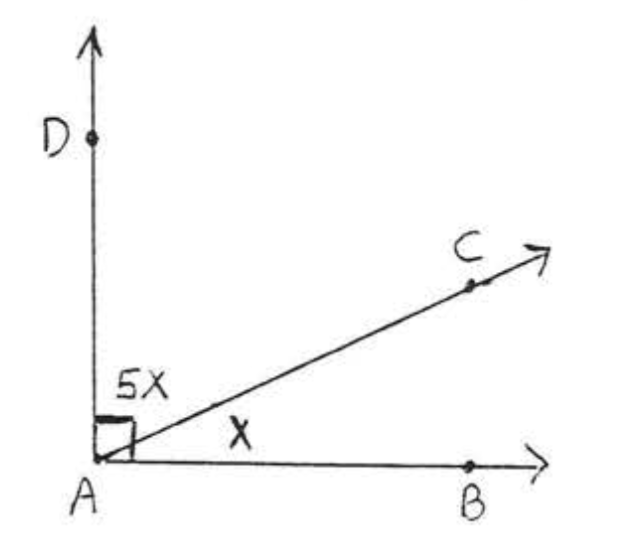 4.
4. 
5.  6.
6. 
7. Encuentra el suplemento de un ángulo de
- \(30^{\circ}\)
- \(37^{\circ}\)
- \(90^{\circ}\)
- \(120^{\circ}\)
8. Encuentra el suplemento de un ángulo de
- \(45^{\circ}\)
- \(52^{\circ}\)
- \(85^{\circ}\)
- \(135^{\circ}\)
9 - 14. Encuentra\(x\) y los ángulos suplementarios:
9. 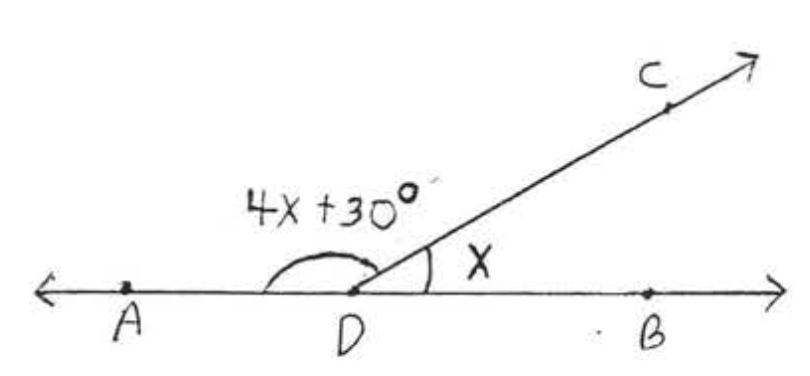 10.
10. 
11.  12.
12. 
13. 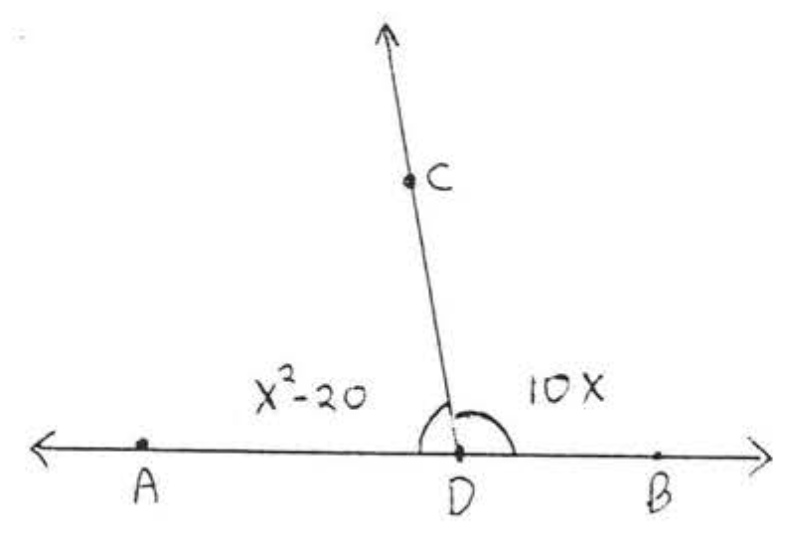 14.
14. 
15 - 22. Buscar\(x, y\), y\(z\):
15.  16.
16. 
17.  18.
18. 
19.  20.
20. 
21.  22.
22. 
23 - 26. Encuentra\(x\):
23.  24.
24. 
25.  26.
26. 
27. Encuentra el ángulo de incidencia,\(\angle CDA\):

28. \(x\)Averigua si el ángulo de incidencia es\(40^{\circ}\):



