1.2: Ángulos
- Page ID
- 114543
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
Un ángulo es la figura formada por dos rayos con un punto final común, Los dos rayos se llaman los lados del ángulo y el punto final común se llama el vértice del ángulo, El símbolo para ángulo es\(\angle\)

El ángulo en Figura\(\PageIndex{1}\) tiene vértice\(A\) y lados\(AB\) y\(AC\), Se denota por\(\angle BAC\) o\(\angle CAB\) o simplemente\(\angle A\). Cuando se usan tres letras, la letra media es siempre el vértice, En Figura no\(\PageIndex{2}\) usaríamos la notación\(\angle A\) como abreviatura\(\angle BAC\) porque también podría significar\(\angle CAD\) o\(\angle BAD\), Sin embargo podríamos usar el nombre más simple\(\angle x\) para\(\angle BAC\) si "\(x\)" es marcado como se muestra,
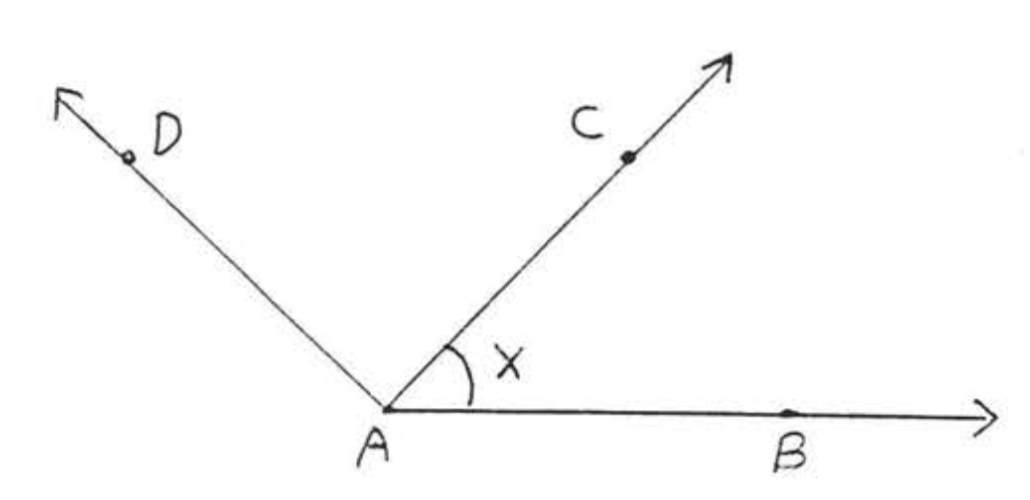
Los ángulos se pueden medir con un instrumento llamado un traslador. La unidad de medida se llama grado y el símbolo para grado es\(^{\circ}\).
Para medir un ángulo, coloca el centro del traslador (a menudo marcado con una cruz o un círculo pequeño) en el vértice del ángulo, Coloca el traslador de manera que un lado del ángulo corte a través de 0, al comienzo de la escala, y para que el otro lado corte a través de un punto más arriba en la escala, Utilizamos ya sea la escala superior o la escala inferior, lo que sea más conveniente, Por ejemplo, en la Figura\(\PageIndex{3}\), un lado de\(\angle BAC\) cruces 0 en la escala inferior y el otro lado cruza 50 en la escala inferior. La medida de\(\angle BAC\) es por lo tanto\(50^{\circ}\) y escribimos\(\angle BAC\) =\(50^{\circ}\).

En la Figura\(\PageIndex{4}\), lado\(\overrightarrow AD\) de\(\angle DAC\) cruces 0 en la escala superior. Por lo tanto, miramos en la escala superior el punto en el que\(\overrightarrow{AC}\) cruza y concluimos que\(\angle DAC = 130^{\circ}\).

Dibuja un ángulo de\(40^{\circ}\) y etiquételo\(\angle BAC\).
Solución
Dibuja rayos\(\overrightarrow{AB}\) usando un borde recto:

Coloca el traslador de manera que su centro coincida\(A\) y\(\overrightarrow{AB}\) cruce la escala a 0:

Marcar el lugar en el traslador correspondiente a\(40^{\circ}\). Marque este punto\(C\):

Conectar\(A\) con\(C\):

Se dice que dos ángulos son iguales si tienen la misma medida en grados. A menudo indicamos que dos ángulos son iguales marcándolos de la misma manera. En Figura\(\PageIndex{5}\),\(\angle A = \angle B\).

Un ángulo bisectriz es un rayo que divide un ángulo en dos ángulos iguales. En la Figura\(\PageIndex{6}\),\(\overrightarrow{AC}\) es un ángulo bisectriz de\(\angle BAD\). También decimos\(\overrightarrow{AC}\) bisectos\(\angle BAD\).

Encuentra\(x\) si\(\overrightarrow{AC}\) bisectas\(\angle BAD\) y\(\angle BAD = 80^{\circ}\):

Solución
\(x^{\circ} = \dfrac{1}{2} \angle BAD = \dfrac{1}{2} (80^{\circ}) = 40^{\circ}\)
Respuesta:\(x = 40\).
\(x\)Averiguar si\(\overrightarrow{AC}\) bisectas\(\angle BAD\):

Solución
\[\begin{array} {rcl} {\angle BAC} & = & {\angle CAD} \\ {\dfrac{7}{2} x} & = & {3x + 5} \\ {(2) \dfrac{7}{2} x} & = & {(2) (3x + 5)} \\ {7x} & = & {6x + 10} \\ {7x - 6x} & = & {10} \\ {x } & = & {10} \end{array}\]
Comprobar:

Respuesta:\(x = 10\).
Problemas
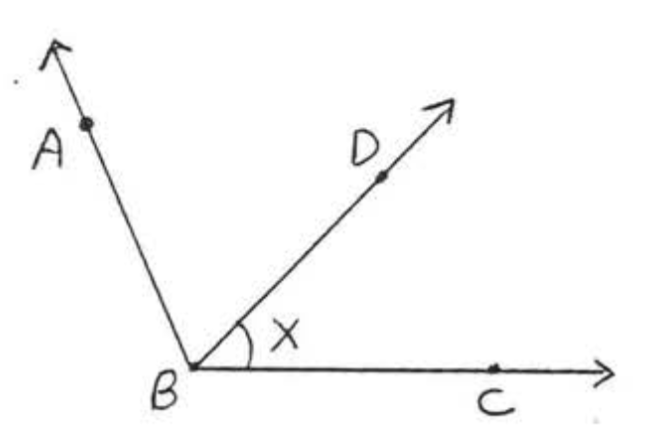
1 - 6. Para cada figura, da otro nombre para\(\angle x\):
1. 
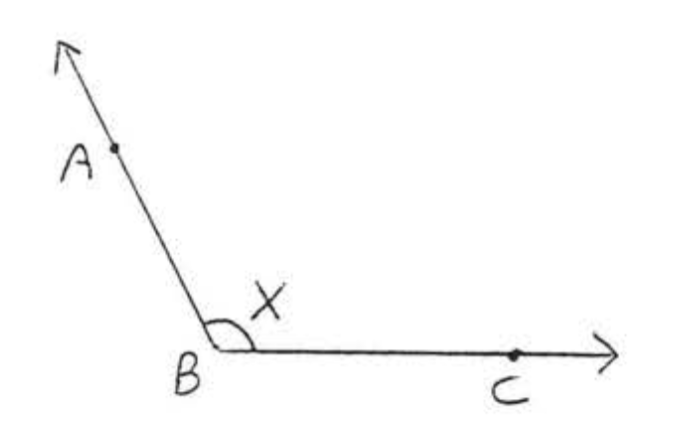
2. 
3. 
4. 
5. 
6. 
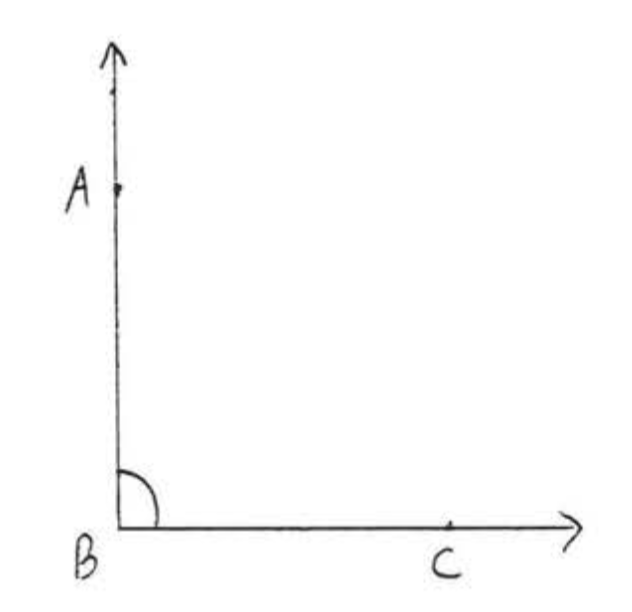
7 - 16, Mida cada uno de los ángulos indicados:
7. 
8. 
9. 
10. 
11. 
12. 
13. 
14. 
15. 
16. 
17 - 24. Dibuje y etiquete cada ángulo:
17. \(\angle BAC = 30^{\circ}\)
18. \(\angle BAC = 40^{\circ}\)
19. \(\angle ABC = 45^{\circ}\)
20. \(\angle EFG = 60^{\circ}\)
21. \(\angle RST = 72^{\circ}\)
22. \(\angle XYZ = 90^{\circ}\)
23. \(\angle PQR = 135^{\circ}\)
24. \(\angle JKL = 164^{\circ}\)
25 - 28. \(x\)Averiguar si\(\overrightarrow{AC}\) bisectas\(\angle BAD\):
25. 
26. 
27. 
28. 


