1.4: Líneas paralelas
- Page ID
- 114553
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
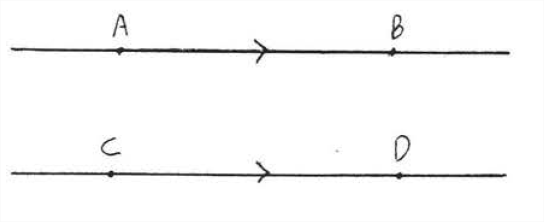
Dos líneas son paralelas si no se encuentran, por muy lejos que estén extendidas. El símbolo para paralelo es\(||\). En Figura\(\PageIndex{1}\),\(\stackrel{\leftrightarrow}{A B}\)\(||\)\(\stackrel{\leftrightarrow}{C D}\). Las marcas de flecha se utilizan para indicar que las líneas son paralelas.
Hacemos la siguiente suposición sobre las líneas paralelas, llamadas postulado paralelo.
Las probabilidades asignadas a eventos por una función de distribución en un espacio muestral están dadas por
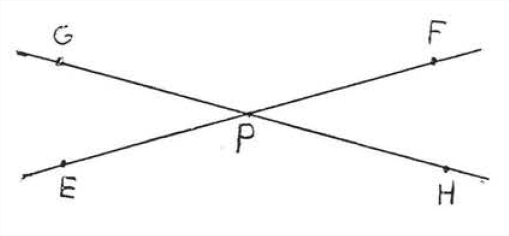
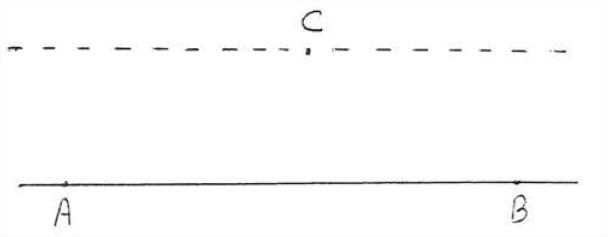
A través de un punto que no esté en una línea dada, se puede dibujar una y solo una línea paralela a la línea dada. Entonces en Figura\(\PageIndex{3}\), hay exactamente una línea que se puede dibujar a través de la\(C\) que es paralela a\(\overleftarrow{\mathrm{AB}}\).
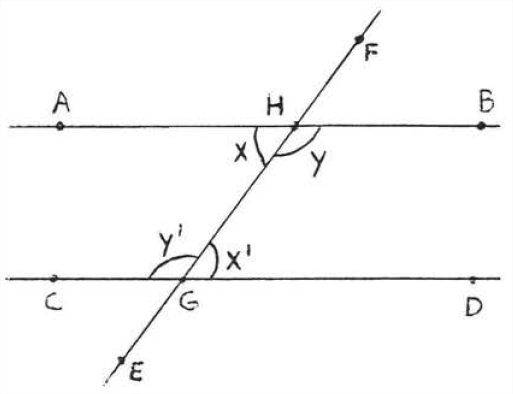
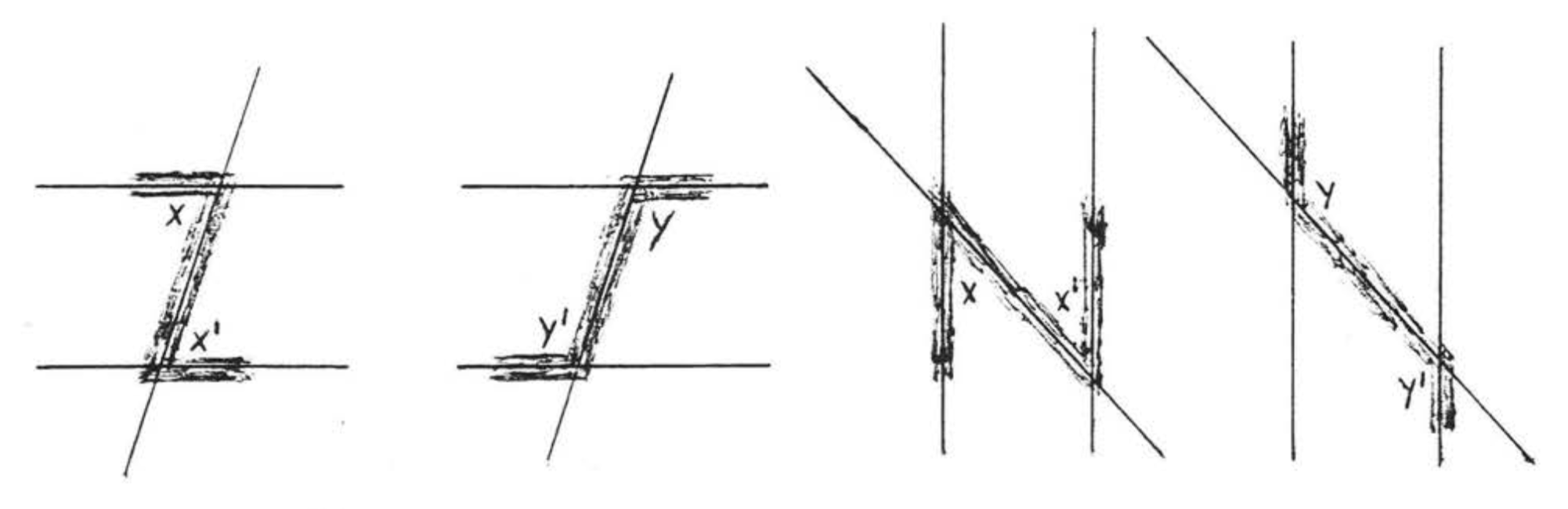
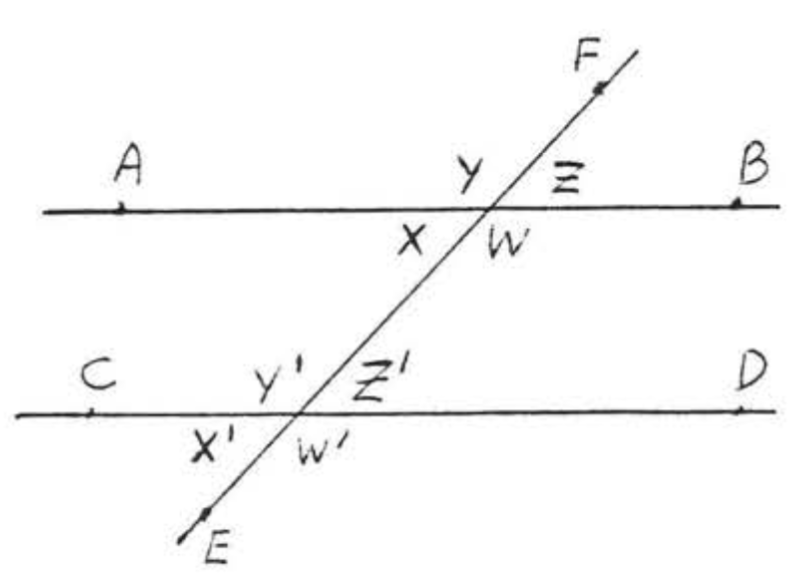
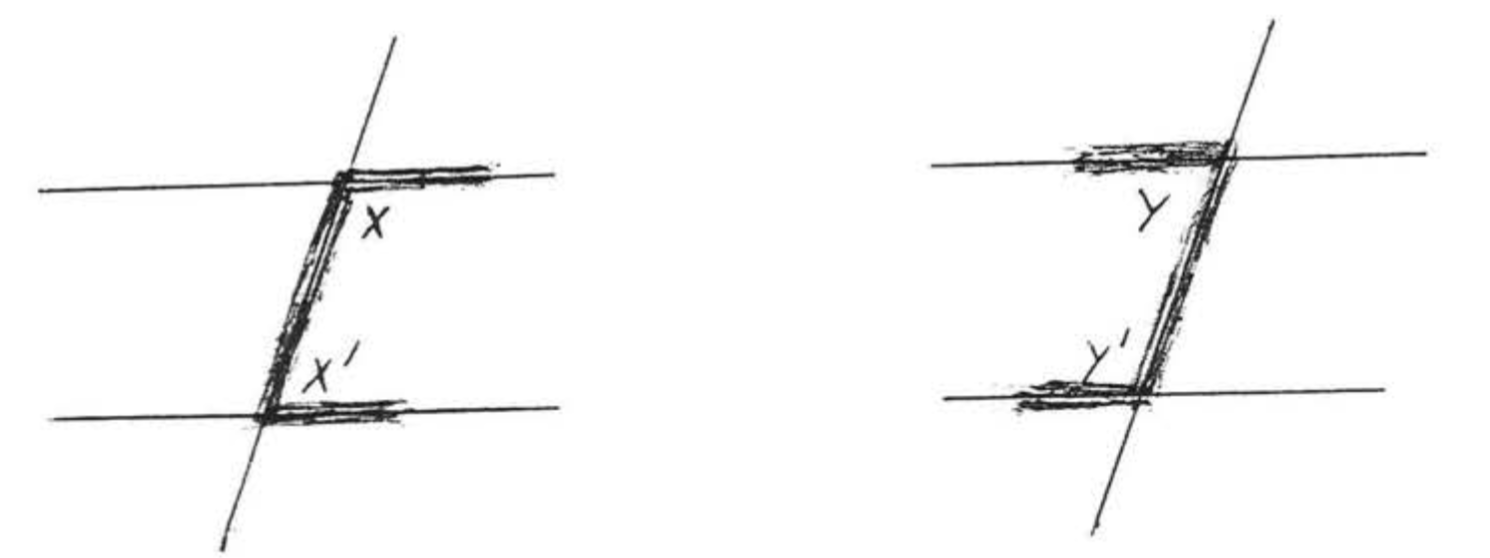
Una transversal es una línea que cruza otras dos líneas en dos puntos distintos. En la Figura\(\PageIndex{4}\),\(\overleftrightarrow{EF}\) es una transversal. \(\angle x\)y\(\angle x^{\prime}\) se llaman ángulos interiores alternos de líneas\(\overleftrightarrow{AB}\) y\(\overleftrightarrow{CD}\). La palabra “alternar”, aquí, significa que los ángulos están en diferentes lados de la transversal, un ángulo formado con\(\overleftrightarrow{AB}\) y el otro formado con\(\overleftrightarrow{CD}\). La palabra “interior” significa que están entre las dos líneas. Observe que forman la letra "”\(Z\). (Figura\(\PageIndex{5}\)). \(\angle y\)y también\(\angle y^{\prime}\) son ángulos interiores alternos. También forman un "\(Z\)" aunque se estira hacia fuera y hacia atrás. Vista desde un lado, la letra "\(Z\)" también puede parecer una "”\(N\).”
Los ángulos interiores alternos son importantes debido al siguiente teorema:
Si dos líneas son paralelas entonces sus ángulos interiores alternos son iguales, Si los ángulos interiores alternos de dos líneas son iguales entonces las líneas deben 'oe paralelas,
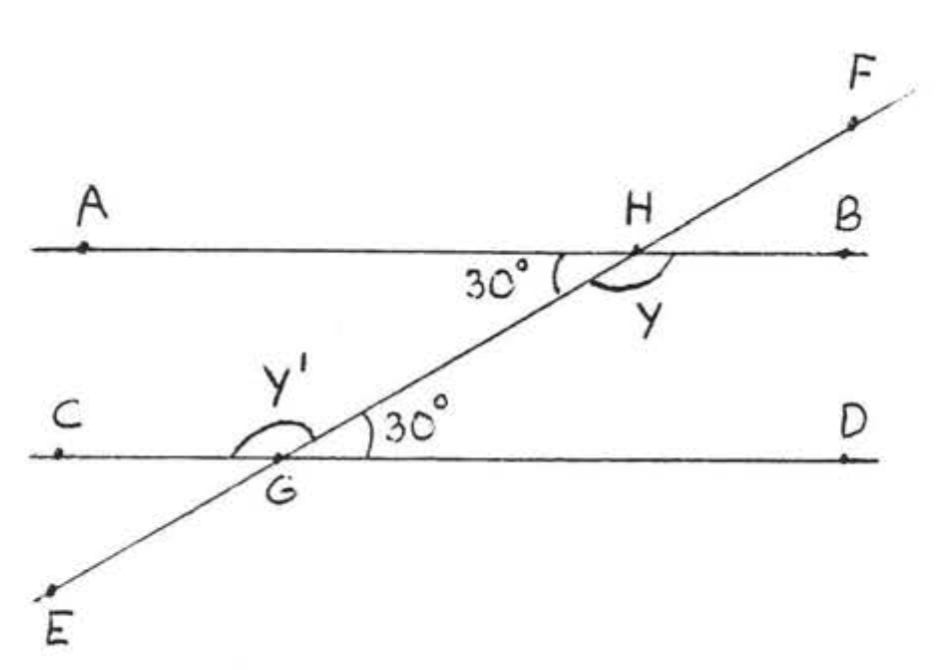
En la Figura\(\PageIndex{6}\),\(\overleftrightarrow{AB}\) debe ser paralelo a\(\overleftrightarrow{CD}\) porque los ángulos interiores alternos son ambos\(30^{\circ}\). Observe que el otro par de ángulos interiores alternos,\(\angle y\) y\(\angle y'\), también son iguales. Ellos son los dos\(150^{\circ}\). En la Figura\(\PageIndex{7}\), las líneas no son paralelas y ninguno de los ángulos interiores alternos son iguales.
La Prueba de Teorema\(\PageIndex{1}\) es complicada y será diferida al apéndice.
Encuentra\(x, y\) y\(z\):
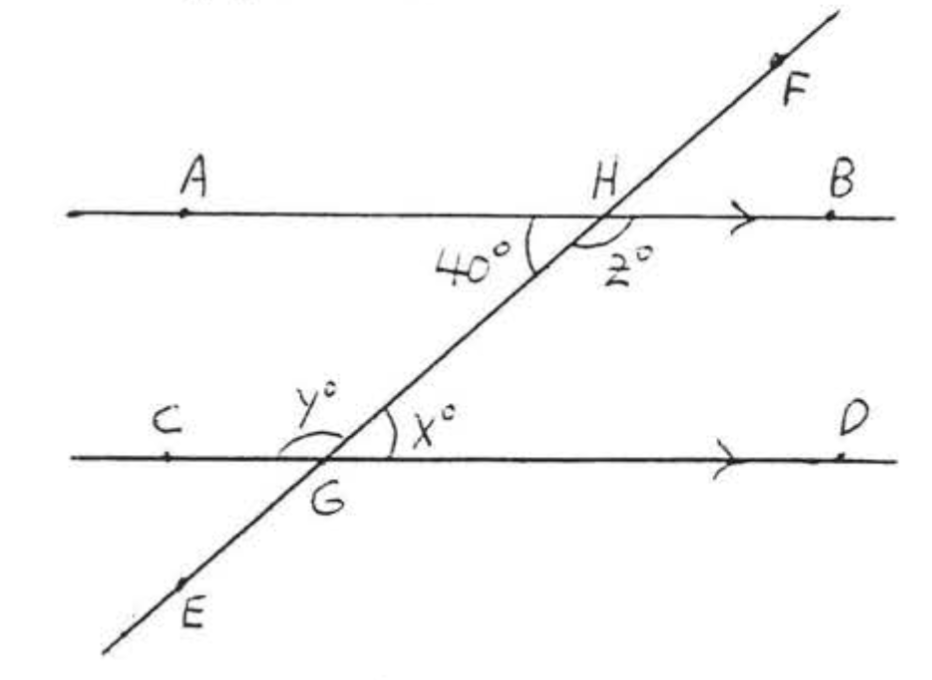
Solución
\(\overleftrightarrow{AB} || \overleftrightarrow{CD}\)ya que las flechas indican líneas paralelas. \(x^{\circ} = 40^{\circ}\)porque los ángulos interiores alternos de las líneas paralelas son iguales. \(y^{\circ} = z^{\circ} = 180^{\circ} - 40^{\circ} = 140^{\circ}\).
Respuesta:\(x = 40, y = 140, z = 140\).
Los ángulos correspondientes de dos líneas son dos ángulos que están en el mismo lado de las dos líneas y el mismo lado de la transversal, En Figura\(\PageIndex{8}\),\(\angle w\) y\(\angle w'\) son ángulos correspondientes de líneas\(\overleftrightarrow{AB}\) y\(\overleftrightarrow{CD}\). Forman la letra "”\(F\). \(\angle x\)y\(\angle x'\),\(\angle y\) y\(\angle y'\), y\(\angle z\) y\(\angle z'\) son otros pares de ángulos correspondientes de\(\overleftrightarrow{AB}\) y\(\overleftrightarrow{CD}\). Todos forman la letra "\(F\)“, aunque podría ser una al revés o al revés"\(F\) "(Figura\(\PageIndex{9}\)).
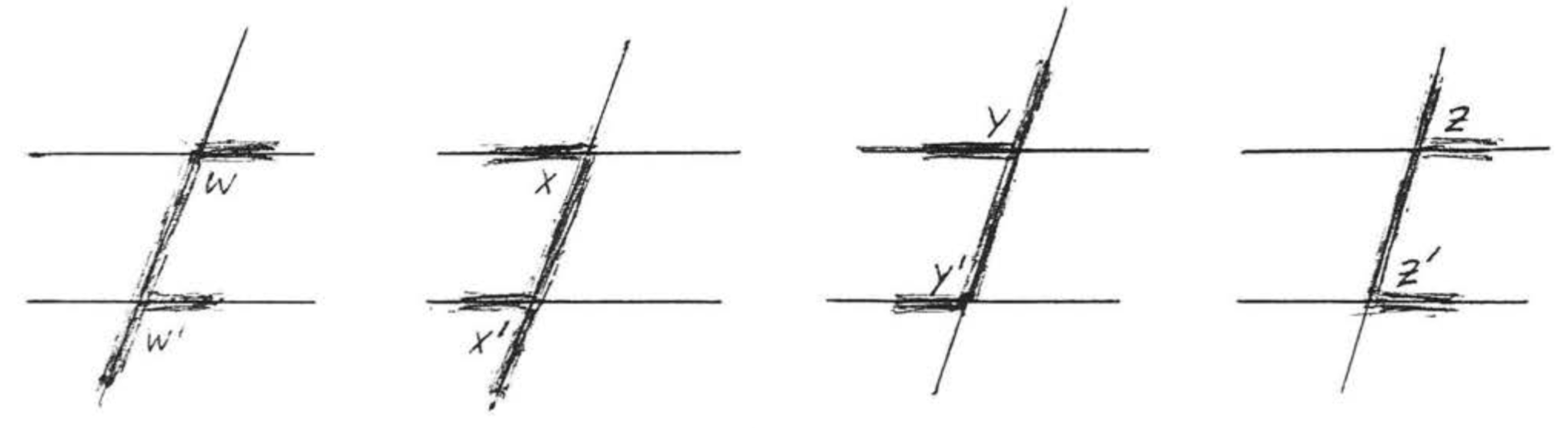
Los ángulos correspondientes son importantes debido al siguiente teorema:
Si dos líneas son paralelas entonces sus ángulos correspondientes son iguales. Si los ángulos correspondientes de dos líneas son iguales entonces las líneas deben ser paralelas.
Encuentra\(x\):
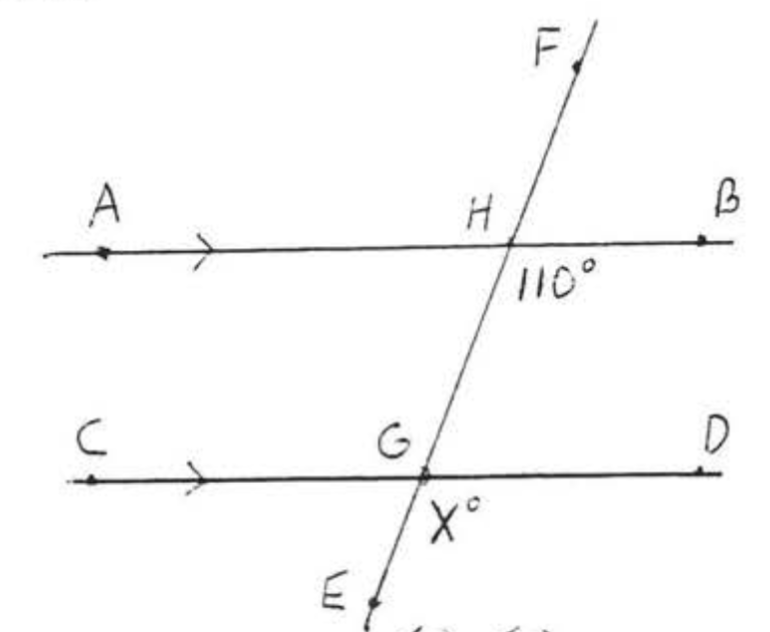
Solución
La flecha indica\(\overleftrightarrow{AB} || \overleftrightarrow{CD}\). Por lo tanto\(x^{\circ} = 110^{\circ}\) porque\(x^{\circ}\) y\(110^{\circ}\) son las medidas de los ángulos correspondientes de las líneas paralelas\(\overleftrightarrow{AB}\) y\(\overleftrightarrow{CD}\).
Respuesta:\(x = 110\).
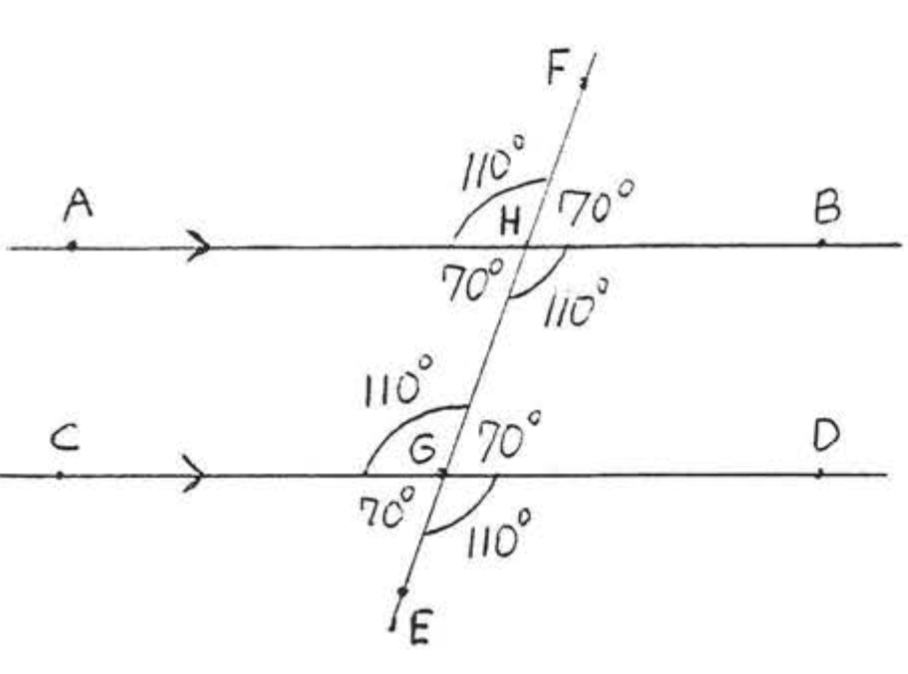
Observe que ahora podemos encontrar todos los demás ángulos en Ejemplo\(PageIndex{2}\). Cada uno es complementario a uno de los\(110^{\circ}\) ángulos o forma ángulos verticales iguales con uno de ellos (Figura\(PageIndex{10}\)). Por lo tanto todos los ángulos correspondientes son iguales, También cada par de ángulos interiores alternos es igual. No es difícil ver que si solo un par de ángulos correspondientes o un par de ángulos interiores alternos son iguales entonces también lo son todos los demás pares de ángulos interiores correspondientes y alternos.
Prueba de Teorema\(\PageIndex{2}\): Los ángulos correspondientes serán iguales si los ángulos interiores alternos son iguales y viceversa. Por lo tanto el teorema\(\PageIndex{2}\) sigue directamente de Therorem\(\PageIndex{1}\).
En la Figura\(\PageIndex{11}\),\(\angle x\) y se\(\angle x'\) denominan ángulos interiores en el mismo lado de la transversal. (En algunos libros de texto, los ángulos interiores en el mismo sdie de la transversal se denominan ángulos cointeriores). \(\angle y\)y también\(\angle y'\) son ángulos interiores en el mismo lado de la transversal, Observe que cada par de ángulos forma la letra "\(C\).” Comparar Figura\(\PageIndex{11}\) con Figura 10 y también con Ejemplo\(\PageIndex{1}\), El siguiente teorema es entonces evidente:
Si dos líneas son paralelas entonces los ángulos interiores en el mismo lado de la transversal son suplementarios (suman hasta\(180^{\circ}\)). Si los ángulos interiores de dos líneas del mismo lado de la transversal son suplementarios entonces las líneas deben ser paralelas.
Encontrar\(x\) y los ángulos marcados:
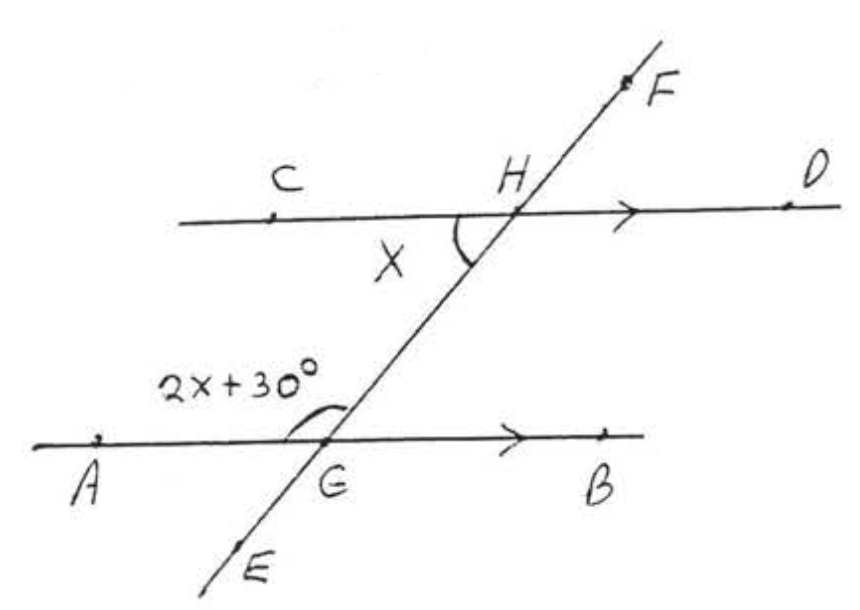
Solución
Las líneas son paralelas así por teorema\(\PageIndex{3}\) the two labelled angles must be supplementary.
\[\begin{array} {rcl} {x + 2x + 30} & = & {180} \\ {3x + 30} & = & {180} \\ {3x} & = & {180 - 30} \\ {3x} & = & {150} \\ {x} & = & {50} \end{array}\]
\(\angle CHG = x = 50^{\circ}\)
\(\angle AGH = 2x + 30 = 2(50) + 30 = 100 + 30 = 130^{\circ}\).
Comprobar:
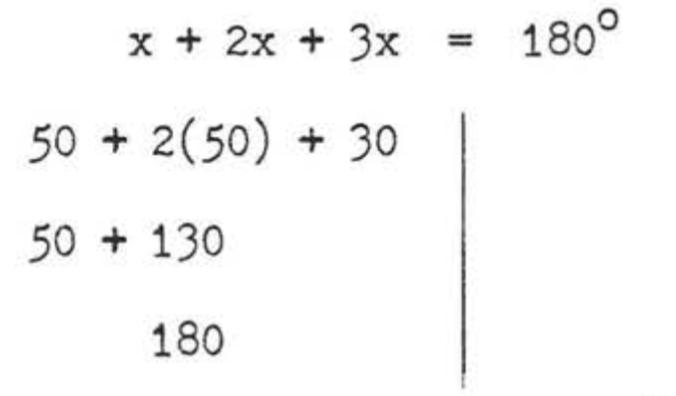
Respuesta:\(x = 50\),\(\angle CHG = 50^{\circ}\),\(\angle AGHa = 130^{\circ}\).
Encontrar\(x\) y los ángulos marcados:
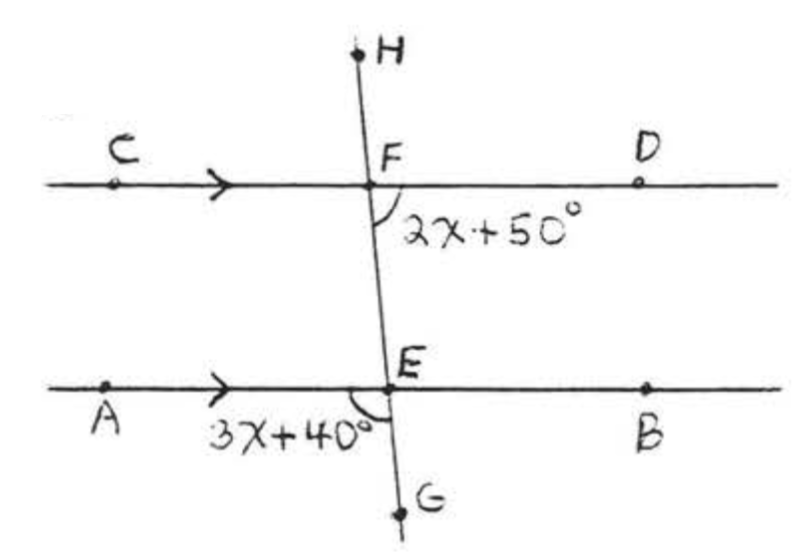
Solución
\(\angle BEF = 3x + 40^{\circ}\)porque los ángulos verticales son iguales. \(\angle BEF\)y\(\angle DFE\) son ángulos interiores en el mismo lado de la transversal, y por lo tanto son complementarios porque las líneas son paralelas.
\[\begin{array} {rcl} {3x + 40 + 2x + 50} & = & {180} \\ {5x + 90} & = & {180} \\ {5x} & = & {180 - 90} \\ {5x} & = & {90} \\ {x} & = & {18} \end{array}\]
\(\angle AEC = 3x + 40 = 3(18) + 40 = 54 + 40 = 94^{\circ}\)
\(\angle DFE = 2x + 50 = 2(18) + 50 = 36 + 50 = 86^{\circ}\)
Comprobar:
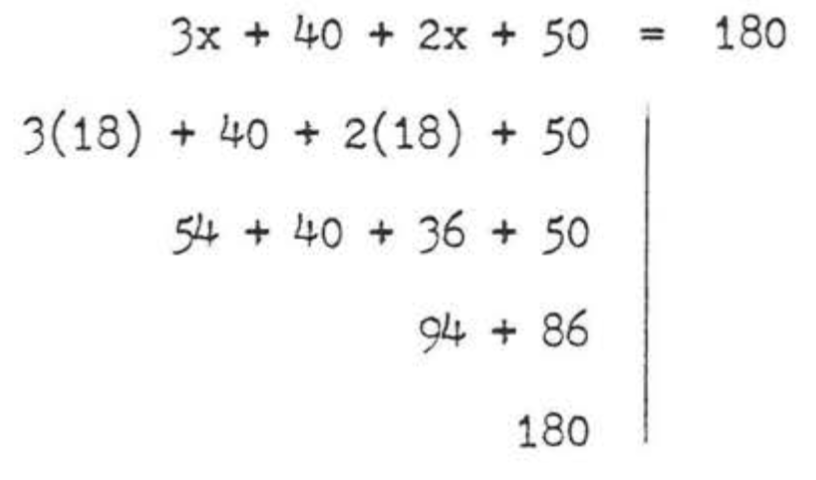
Respuesta:\(x = 18\),\(\angle AEG = 94^{\circ}\),\(\angle DFE = 86^{\circ}\).
Enumere todos los pares de ángulos interiores alternos en el diagrama, (La flecha simple indica que\(\overleftrightarrow{AB}\) es paralela a\(\overleftrightarrow{CD}\) y la flecha doble indica que\(\overleftrightarrow{AD}\) es paralela a\(\overleftrightarrow{BC}\).

Solución
Vemos si una letra\(Z\) o se\(N\) puede formar usando los segmentos de línea en el diagrama (Figura\(\PageIndex{12}\)),
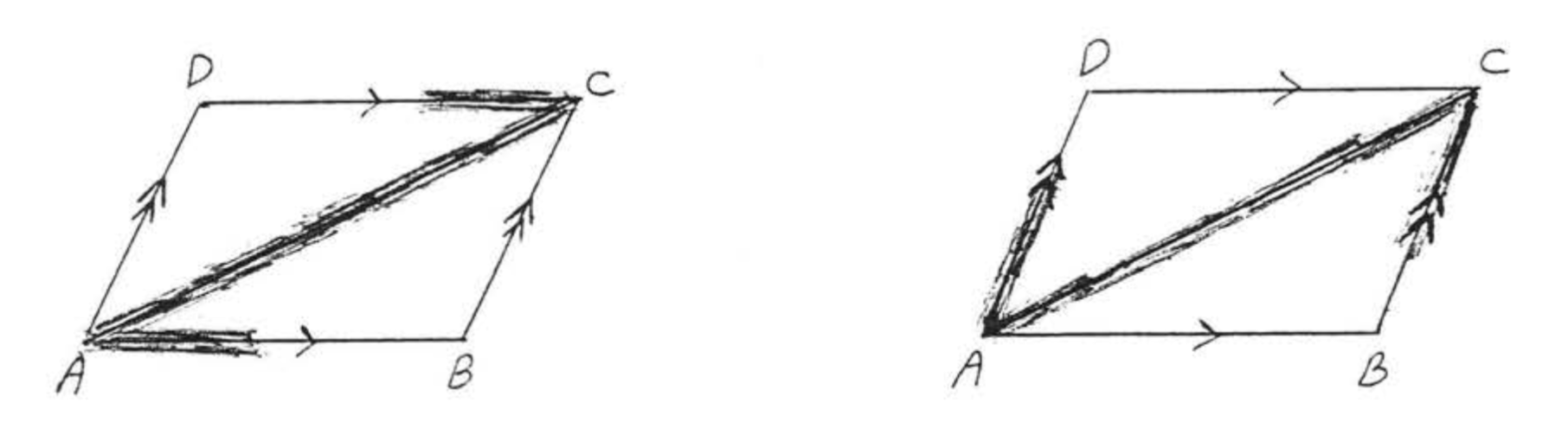
Respuesta:\(\angle DCA\) y\(\angle CAB\) son ángulos interiores alternos de líneas\(\overleftrightarrow{AB}\) y\(\overleftrightarrow{CD}\). \(\angle DAC\)y\(\angle ACB\) son ángulos interiores alternativos de líneas\(\overleftrightarrow{AD}\) y\(\overleftrightarrow{BC}\)
Un telescopio apunta a una estrella\(70^{\circ}\) sobre el horizonte, ¿Qué ángulo\(x^{\circ}\) debe\(BD\) hacer el espejo con la horizontal para que la estrella pueda verse en el ocular\(E\)?
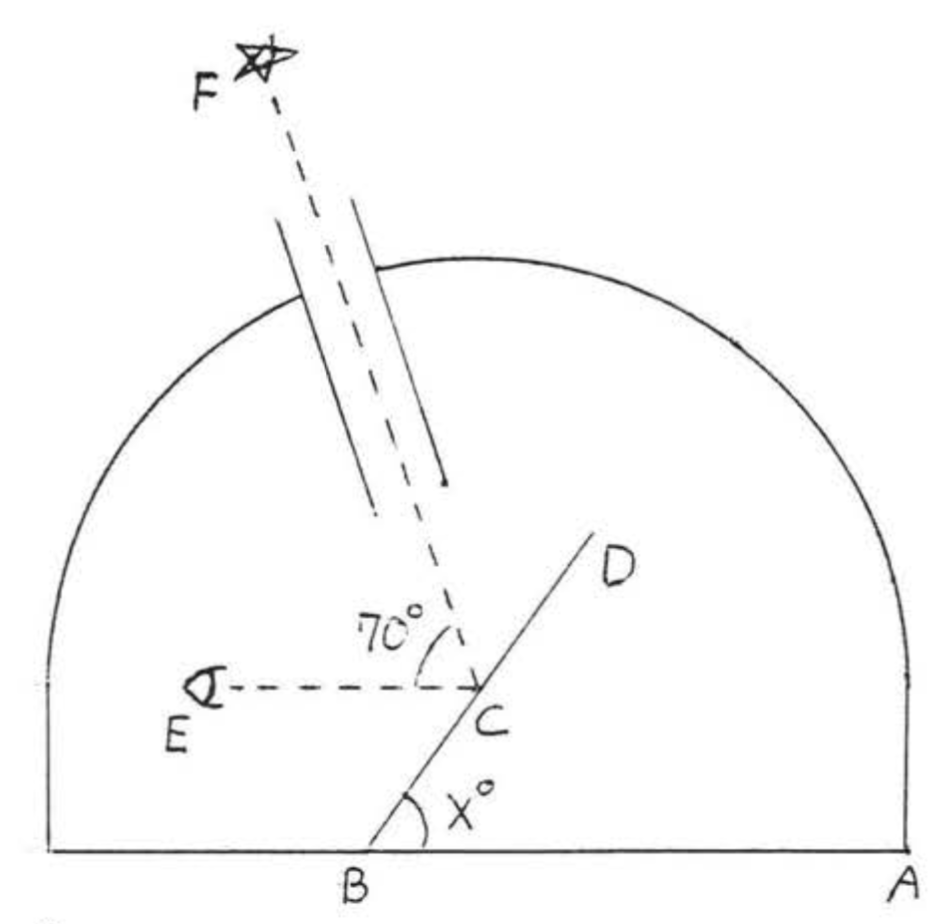
Solución
\(x^{\circ} = \angle BCE\)porque son ángulos interiores alternos de líneas paralelas\(\overleftrightarrow{AB}\) y\(\overleftrightarrow{CE}\). \(\angle DCF = \angle BCE = x^{\circ}\)porque el ángulo de incidencia es igual al ángulo de reflexión. Por lo tanto
\[\begin{array} {rcl} {x + 70 + x} & = & {180} \\ {2x + 70} & = & {180} \\ {2x} & = & {110} \\ {x} & = & {55} \end{array}\]
Respuesta:\(55^{\circ}\)
RESUMEN

Los ángulos interiores alternos de las líneas paralle son iguales. Forman la letra "”\(Z\).
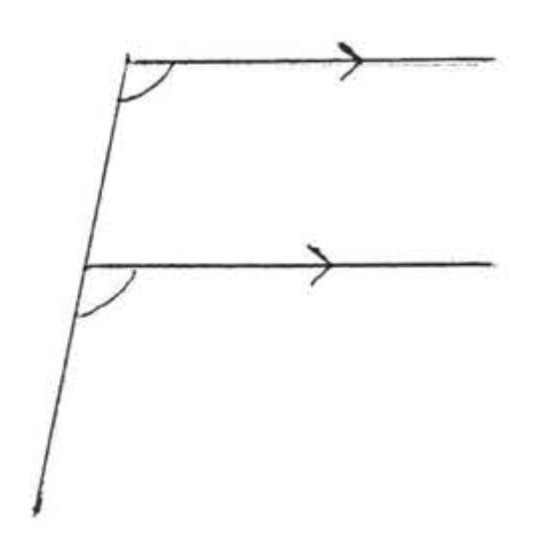
Los ángulos correspondientes de las líneas paralelas son iguales. Forman la letra "”\(F\).
Los ángulos interiores en los mismos lados de la transversal de las líneas paralelas son suplementarios. Forman la letra "”\(G\).
El postulado paralelo dado anteriormente en esta sección es el equivalente al quinto postulado de los Elementos de Euclides. Euclides tenía razón al asumirlo como un postulado en lugar de intentar probarlo como teorema, sin embargo esto no quedó claro para el mundo matemático hasta el siglo XIX, 2200 años después, En el ínterin, decenas de destacados matemáticos intentaron sin éxito dar una prueba satisfactoria de la postulado paralelo. Consideraban que no era tan evidente como debería ser un postulado y que requería alguna justificación formal,
En 1826, N, I, Lobachevsky, matemático ruso, presentó un sistema de geometría basado en el supuesto de que a través de un punto dado se puede dibujar más de una línea recta paralela a una línea dada (Figura\(\PageIndex{13}\)). En 1854, el matemático alemán Georg Bernhard Riemann profoso un sistema de GeometriJ en el que no hay líneas paralelas en absoluto, Una gecmetría en la que el postulado paralelo ha sido sustituido por algún otro postulado se llama geometría no euclidiana. La existencia de estas geometrías muestra que el postulado paralelo no necesariamente tiene que ser cierto. De hecho, Einstein utilizó la geometría de Riemann como base para su teoría de la relatividad.

Por supuesto nuestro postulado paralelo original tiene más sentido para las aplicaciones ordinarias, y lo usamos a lo largo de este libro, Sin embargo, para aplicaciones donde están involucradas grandes distancias, como en astronomía, bien puede ser que una geometría no euclidiana dé una mejor aproximación de la realidad física.
Problemas
Para cada uno de los siguientes enunciar el/los teorema (s) utilizado (es) para obtener su respuesta (por ejemplo, “los ángulos interiores alternos de las líneas paralelas son iguales”). Se supone que las líneas marcadas con la misma flecha son paralelas,
1 - 2. Buscar\(x, y\), y\(z\):
1.  2.
2. 
3 - 4. Buscar\(t\),\(u\),\(v\)\(w\),\(x\),\(y\), y\(z\):
3.  4.
4. 
5 - 10. Encuentra\(x\):
5.  6.
6. 
7.  8.
8. 
9.  10.
10. 
11 - 18. Encontrar\(x\) y los ángulos marcados:
11.  12.
12. 
13.  14.
14. 
15.  16.
16. 
17.  18.
18. 
19 - 26. Para cada uno de los siguientes, enumere todos los pares de ángulos interiores alternos y ángulos correspondientes, Si no los hay, entonces enumere todos los pares de ángulos interiores en el mismo lado de la transversal. Indicar las líneas paralelas que forman cada par de ángulos.
19.  20.
20. 
21.  22.
22. 
23.  24.
24. 
25.  26.
26. 
27. Un telescopio apunta a una estrella\(50^{\circ}\) sobre el horizonte. ¿Qué ángulo\(x^{\circ}\) debe\(BD\) hacer el espejo con la horizontal para que la estrella pueda verse en el ocular\(E\)?

28. Un periscopio es utilizado por los marineros en un submarino para ver objetos en la superficie del agua, Si\(\angle ECF = 90^{\circ}\), ¿qué ángulo\(x^{\circ}\) hace el espejo\(BD\) con la horizontal?



