2.2: El Teorema SAS

Última actualización
Guardar como PDF

Page ID: 114586

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Hemos dicho que dos triángulos son congruentes si todos sus lados y ángulos correspondientes son iguales, sin embargo en algunos casos, es posible concluir que dos triángulos son congruentes, con sólo información parcial sobre sus lados y ángulos.

Supongamos que nos dicen que$\triangle ABC$ tiene$\angle A = 53^{\circ}$,$AB = 5$ pulgadas y$AC = 3$ pulgadas. Vamos a atender a bosquejo$\triangle ABC$. Primero dibujamos un ángulo de$53^{\circ}$ con un trasportador y lo etiquetamos$\angle A$. Usando una regla, encontramos el punto a 5 pulgadas del vértice en un lado del ángulo y lo etiquetamos$B$, En el otro lado del ángulo, encontramos el punto a 3 pulgadas del vértice y lo etiquetamos$C$, Ver Figura$\PageIndex{1}$, Ahora solo hay una forma de completar nuestro boceto de$\triangle ABC$, y es decir para conectar puntos$B$ y$C$ con un segmento de línea, Ahora podríamos medir$BC$$\angle B$,, y$\angle C$ para encontrar las partes restantes del triángulo.

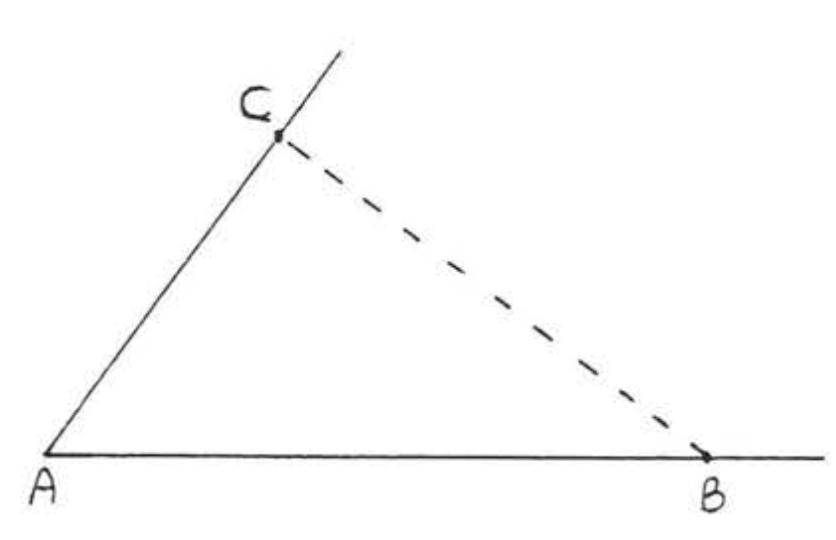
2020-10-30 3.03.10.png — Figura$\PageIndex{1}$: Croquizado$\triangle ABC$.

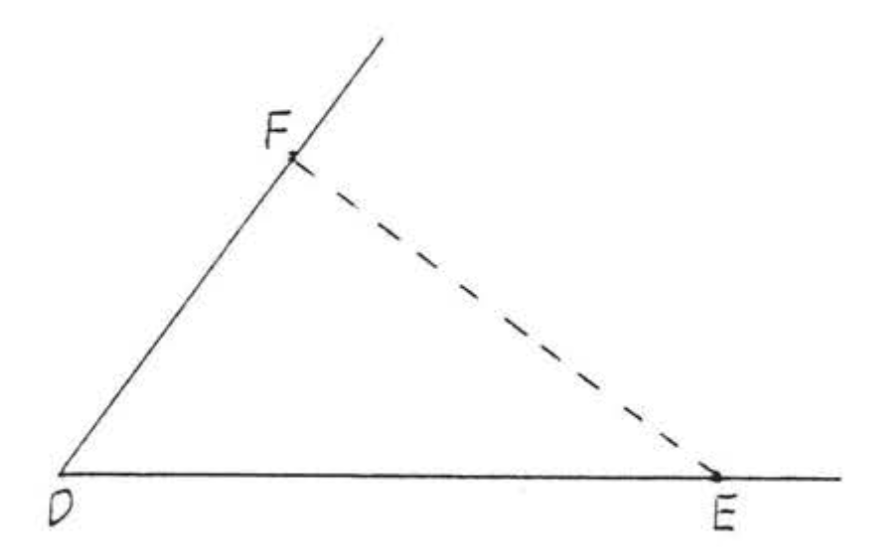
2020-10-30 3.04.09.png — Figura$\PageIndex{2}$: Croquizado$\triangle DEF$.

Supongamos que ahora$\triangle DEF$ eran otro triángulo$\angle D = 53^{\circ}$, con,$DE = 5$ pulgadas y$DF = 3$ pulgadas. Podríamos esbozar$\triangle DEF$ tal como lo hicimos$\triangle ABC$, y luego medir$EF$,$\angle E$, y$\angle F$ (Figura$\PageIndex{2}$). Es claro que debemos tener$BC = EF$,$\angle B = \angle E$, y$\angle C = \angle F$ porque ambos triángulos fueron dibujados exactamente de la misma manera. Por lo tanto$\triangle ABC \cong \triangle DEF$.

En$\triangle ABC$, decimos que$\angle A$ es el ángulo incluido entre lados$AB$ y$AC$.
En$\triangle DEF$, decimos que$\angle D$ es el ángulo incluido entre lados$DE$ y$DF$.

Nuestra discusión sugiere el siguiente teorema:

Teorema$\PageIndex{1}$ (SAS or Side-Angle-Side Theorem)

Dos triángulos son congruentes si dos lados y el ángulo incluido de uno son iguales respectivamente a dos lados y el ángulo incluido del otro,

En la Figura$\PageIndex{1}$ and $\PageIndex{2}$, $\triangle ABC \cong \triangle DEF$ because $AB, AC$, and $\angle A$ are equal respectively to $DE, DF$ and $\angle D$.

A veces abreviamos Teorema simplemente$\PageIndex{1}$ escribiendo$SAS = SAS$.

Ejemplo$\PageIndex{1}$

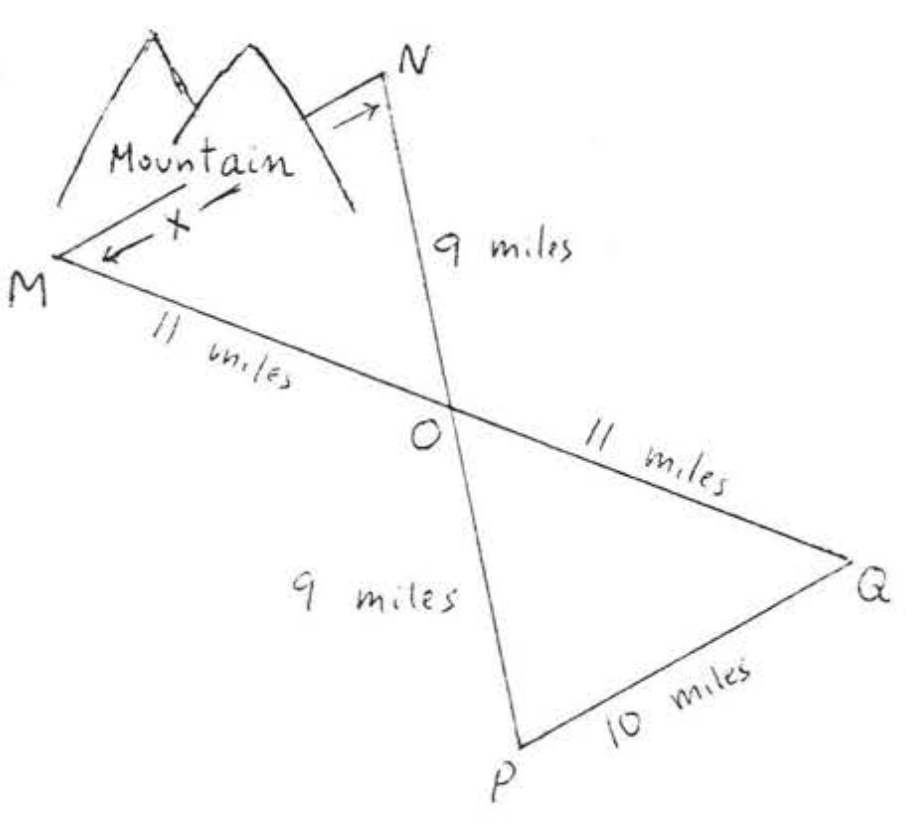
En$\triangle PQR$ nombre el ángulo incluido entre lados

$PQ$y$QR$,
$PQ$y$PR$,
$PR$y$QR$,

Solución

Tenga en cuenta que el ángulo incluido es nombrado por la letra que es común a ambos lados, Para (1), la letra$Q$ "" es común a$PQ$$QR$ y así$\angle Q$ se incluye entre lados$PQ$ y$QR$. De manera similar para (2) y (3).

Respuesta: (1)$\angle Q$, (2)$\angle P$, (3)$\angle R$.

Ejemplo$\PageIndex{2}$

Para los dos triángulos en el diagrama

enumerar dos lados y un ángulo incluido de cada triángulo que son respectivamente iguales, usando la información dada en el diagrama,
escribir la declaración de congruencia,

y (3) encontrar$x$ identificando un par de lados correspondientes de los triángulos congruentes.

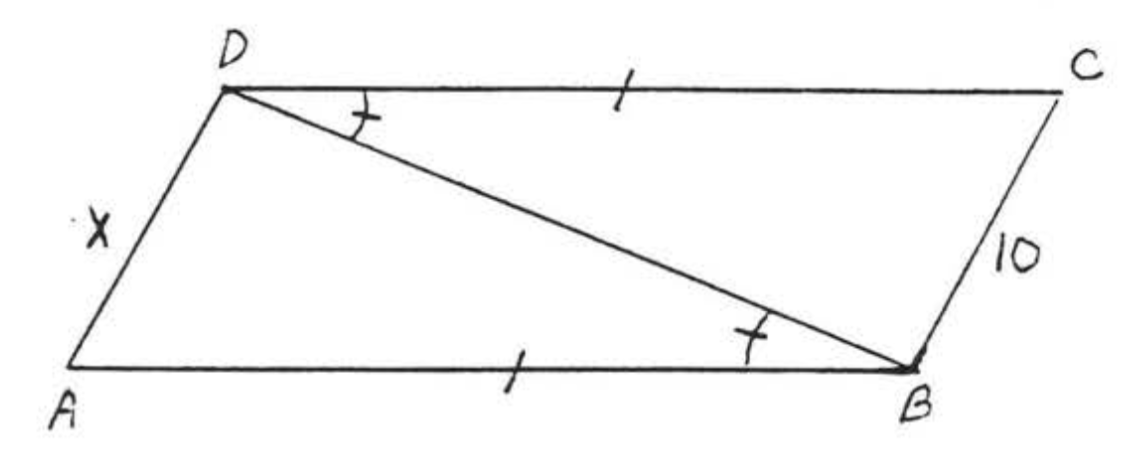
$2020-10-30 3.17.42.png$

Solución

(1) Se supone que los ángulos y lados que se marcan de la misma manera en el diagrama son iguales, Entonces$\angle B$ in$\triangle ABD$ es igual a$\angle D$ in$\triangle BCD$. Por lo tanto,$B$ "" corresponde a "”$D$.” También tenemos$AB = CD$. Por lo tanto$A$ "" debe corresponder a "$C$”. Así, si los triángulos son congruentes, la correspondencia debe ser

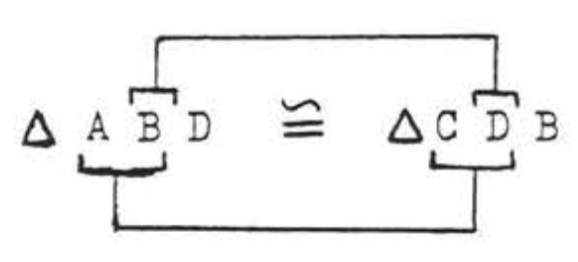
$2020-10-30 3.21.21.png$

Por último,$BD$ (lo mismo que$DB$) es un lado común a ambos triángulos, Summaryzing,

$\begin{array} {ccrclcl} {} & \ & {\underline{\triangle ABD}} & \ & {\underline{\triangle CDB}} & \ & {} \\ {\text{Side}} & \ & {AB} & = & {CD} & \ & {\text{(marked = in diagram)}} \\ {\text{Included Angle}} & \ & {\angle B} & = & {\angle D} & \ & {\text{(marked = in diagram)}} \\ {\text{Side}} & \ & {BD} & = & {DB} & \ & {\text{(common side)}} \end{array}$

(2)$\triangle ABD \cong \triangle CDB$ por el Teorema SAS ($SAS = SAS$).

(3)$x = AD = CB = 10$ porque$AD$ y$CB$ son lados correspondientes (primera y tercera letra en la declaración de congruencia) a.~d lados correspondientes de triángulos congruentes son iguales.

Respuesta:

(1)$AB$,$\angle B$,$BD$ de$\triangle ABD = CD$,$\angle D$,$DB$ de$\triangle CDB$.

(2)$\triangle ABD \cong \triangle CDB$.

(3)$x = AD = CB = 10$.

Ejemplo$\PageIndex{3}$

Para los dos triángulos en el diagrama

enumerar dos lados y un ángulo incluido de cada triángulo que son respectivamente iguales, utilizando la información dada en el diagrama.
escribir la declaración de congruencia, y
encontrar$x$ e$y$ identificar un par de lados correspondientes de los triángulos congruentes.

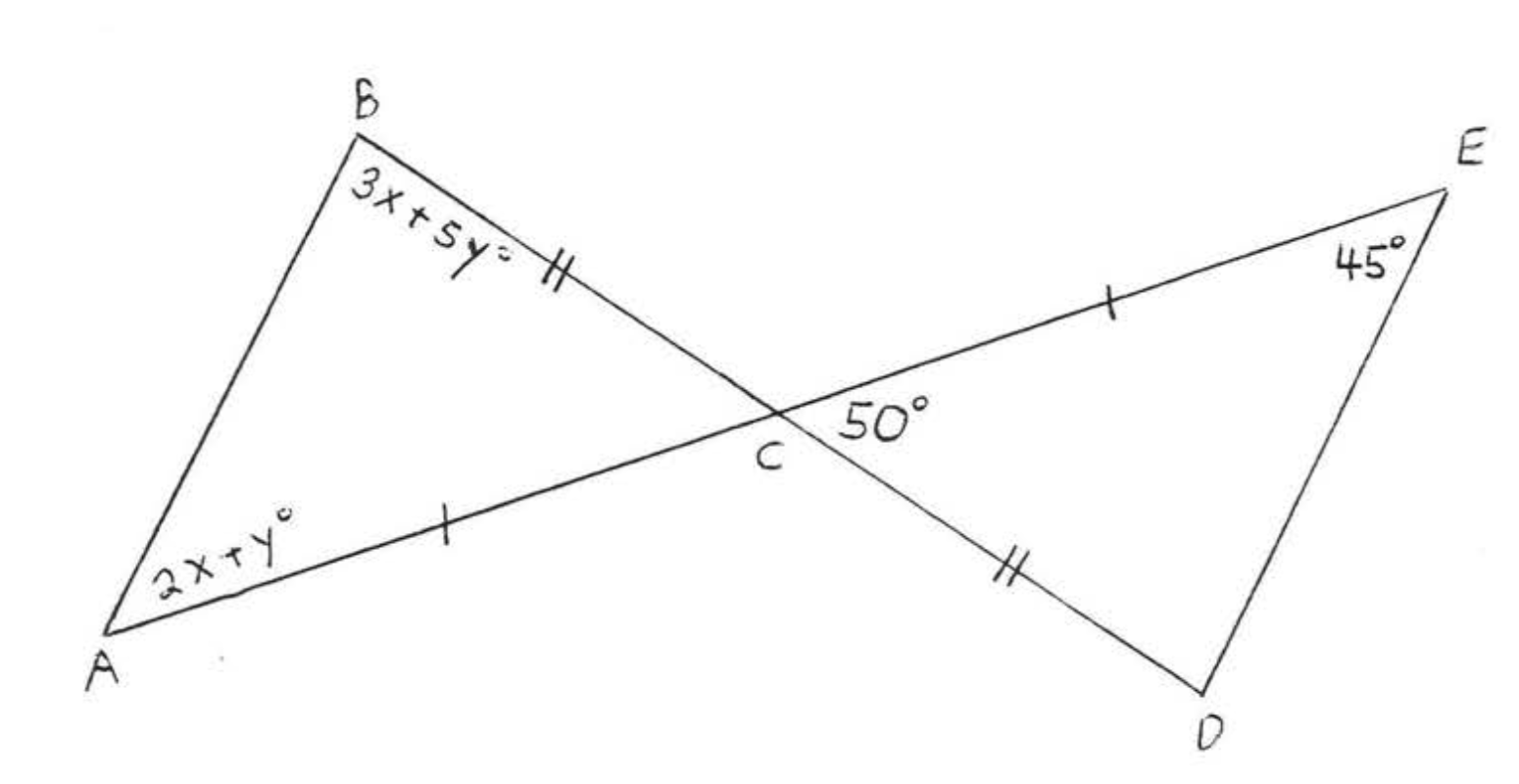
$2020-10-30 3.34.32.png$

Solución

(1)$AC = CE$ y$BC = CD$ porque son mar! ,; :ed de la misma manera. También lo sabemos$\angle ACB = \angle ECD = 50^{\circ}$ porque los ángulos verticales son iguales. Por lo tanto$C$ "" en$\triangle ABC$ corresponde a "$C$" en$\triangle CDE$. Ya que$AC = CE$, debemos tener que "$A$" en$\triangle ABC$ corresponde a "$E$" en$\triangle CDE$. Así, si los triángulos son congruentes, la correspondencia debe ser

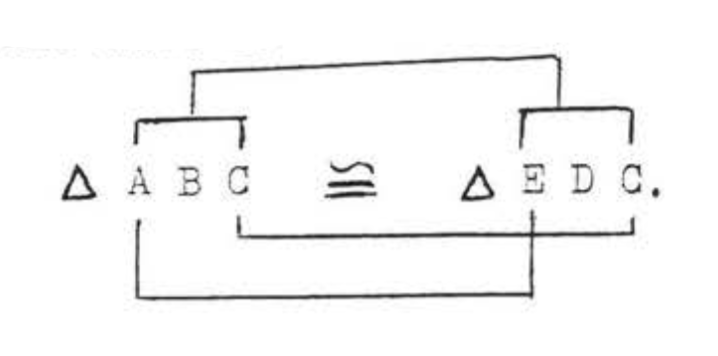
$2020-10-30 3.41.57.png$

Resumimos:

$\begin{array} {ccrclcl} {} & \ & {\underline{\triangle ABC}} & \ & {\underline{\triangle EDC}} & \ & {} \\ {\text{Side}} & \ & {AC} & = & {EC} & \ & {\text{(marked = in diagram)}} \\ {\text{Included Angle}} & \ & {\angle ACB} & = & {\angle ECD} & \ & {\text{(vertical angles are =)}} \\ {\text{Side}} & \ & {BC} & = & {DC} & \ & {\text{(marked = in diagram)}} \end{array}$

(2)$\triangle ABC \cong \triangle EDC$ por el teorema del SAS. ($SAS = SAS$)

(3)$\angle A = \angle E$ y$\angle B = \angle D$ porque son corres:9ángulos onding de los triángulos congruentes. $\angle D = 85^{\circ}$porque la suma de los ángulos de$\triangle EDC$ debe ser$180^{\circ}$. ($\angle D = 180^{\circ} - (50^{\circ} + 45^{\circ}) = 180^{\circ} - 95^{\circ} = 85^{\circ}$). Obtenemos un sistema de dos ecuaciones en las dos incógnitas$x$ y$y$:

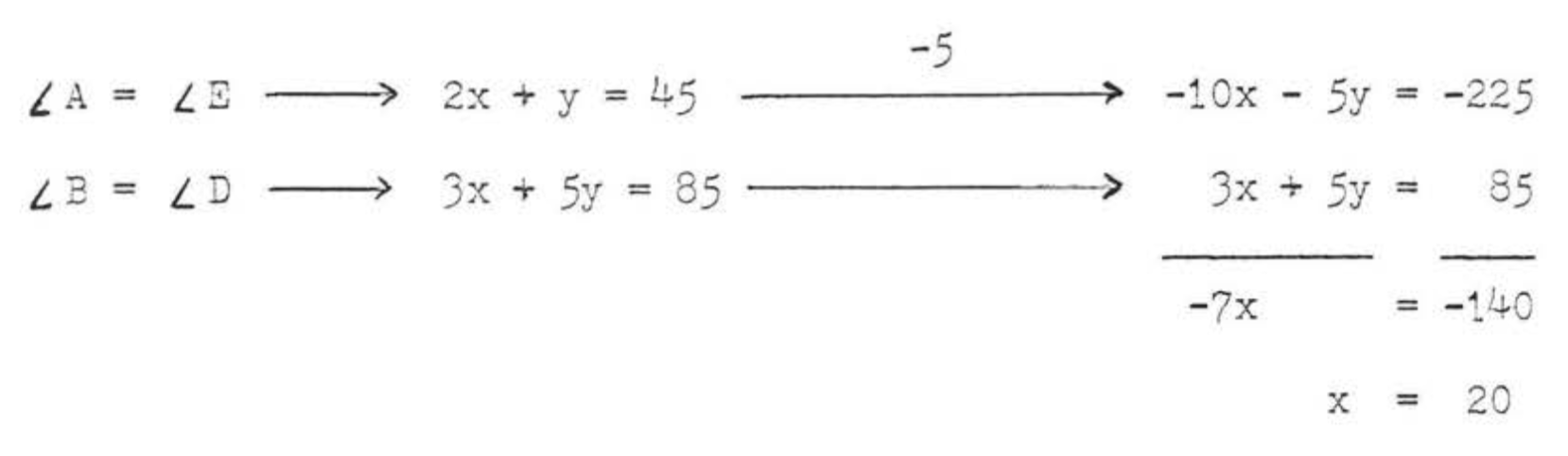
$2020-10-30 3.46.35.png$

Sustituyendo$x$ en la primera ecuación original,

\[\begin{array} {rcl} {2x + y} & = & {45} \\ {2(20) + y} & = & {45} \\ {40 + y} & = & {45} \\ {y} & = & {45- 40} \\ {y} & = & {5} \end{array}\]

Comprobar:

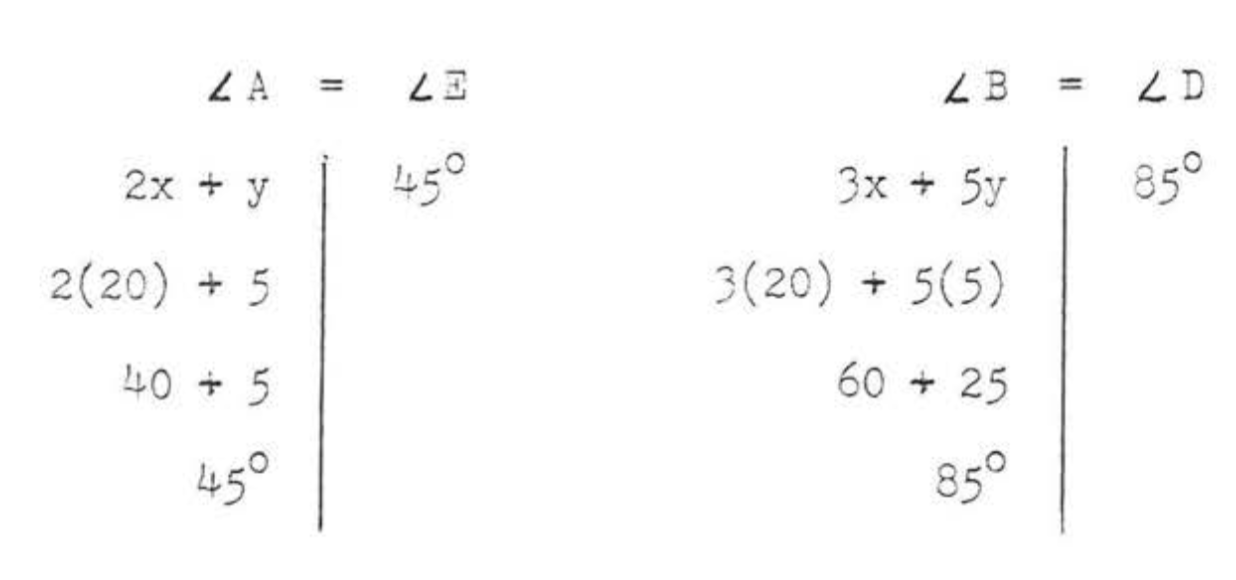
$2020-10-30 3.50.00.png$

Respuesta:

$AC$,$\angle ACB$,$BC$ de$\triangle ABC$ =$EC, \angle ECD, DC$ de$\triangle EDC$.
$\triangle ABC \cong \triangle EDC$.
$x = 20, y = 5$.

Ejemplo$\PageIndex{4}$

Se utilizó el siguiente procedimiento para medir el d.istance AB a través de un estanque: A partir de un punto$C$,$AC$ y se$BC$ midieron y encontraron 80 y 100 pies respectivamente. Después$AC$ se extendió a$E$ así que$AC = CE$ y$BC$ se extendió a para$D$ que$BC = CD$. Finalmente,$DE$ encontramos ser de 110 pies.

Escribe la declaración de congruencia.
Dar una razón para (1).
Encontrar$AB$.

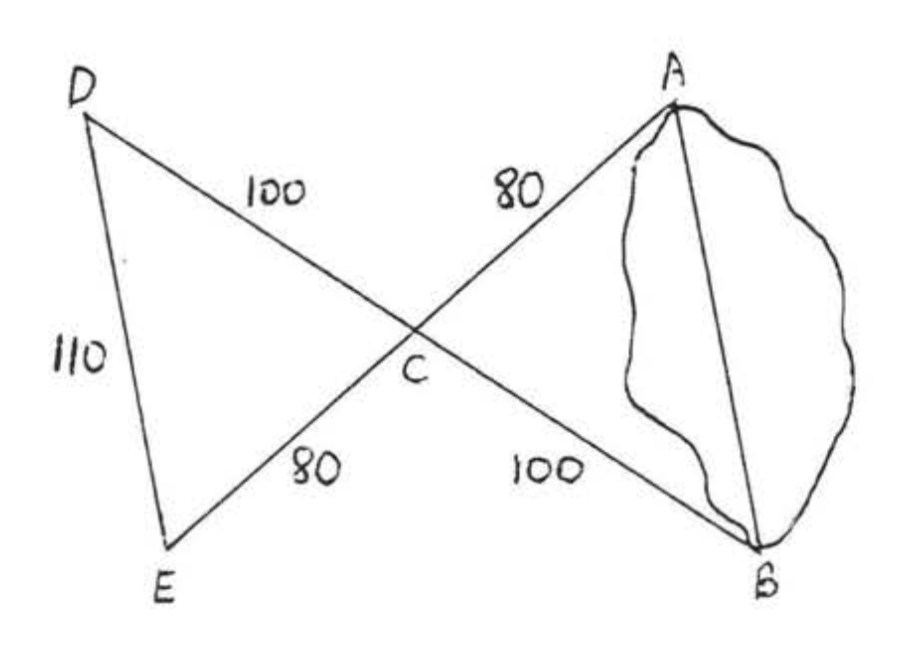
$2020-10-30 3.55.21.png$

Solución

(1)$\angle ACB = \angle ECD$ porque los ángulos verticales son iguales. Por lo tanto los "$C$'s” corresponden,$AC = EC$ así$A$ deben corresponder a$E$. Tenemos

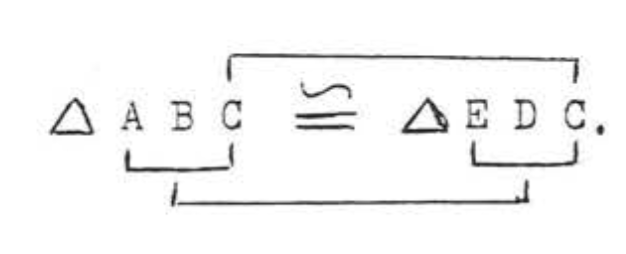
$2020-10-30 3.56.25.png$

(2)$SAS = SAS$. Los lados$AC$$BC$,, y el ángulo incluido$C$ de$ABC$ son iguales respectivamente a$EC, DC$, y ángulo incluido$C$ de$\angle EDC$.

(3)$AB = ED$ porque son lados correspondientes de triángulos congruentes, Desde$ED = 110$,$AB = 110$.

Responder

(1)$\triangle ABC \cong \triangle EDC$.

(2)$SAS = SAS$:$AC$,$\angle C$,$BC$ de$\triangle ABC = EC$,$\angle C$,$DC$ de$\triangle EDC$.

(3)$AB = 110 feet$.

Nota Histórica

El Teorema SAS es la Proposición 4 en los Elementos de Euclides, Tanto nuestra discusión como la prueba de Suclit del Teorema del SAS utilizan lícitamente el siguiente principio: Si una construcción geométrica se repite en una ubicación diferente (o lo que equivale a lo mismo se “mueve” a una ubicación diferente) entonces el tamaño y forma de la figura siguen siendo los mismos, Hay evidencia de que Euclides utilizó este principio a regañadientes, y muchos matemáticos desde entonces han cuestionado su uso en pruebas formales, Sienten que hace una suposición demasiado fuerte sobre la naturaleza del espacio físico y es una forma inferior de razonamiento geométrico. Bertrand Russell (1872 - 1970), por ejemplo, ha sugerido que sería mejor asumir el Teorema SAS como postulado, Esto se hace de hecho en un sistema de axiomas para geometría euclidiana ideado por David Hilbert (1862 - 1943), sistema que ha ganado mucho favor con los matemáticos modernos. Hilbert fue el exponente principal de la “escuela formalista”, que buscaba descubrir exactamente qué supuestos subyacen a cada rama de las matemáticas y eliminar todas las ambigüedades lógicas, el sistema de Hilbert, sin embargo, es demasiado formal para un curso introductorio en geometría,

Problemas

1 - 4. Para cada uno de los siguientes (1) dibujar el triángulo con los dos lados y el ángulo incluido y (2) medir el lado restante y los ángulos:

1. $AB = 2$pulgadas,$AC = 1$ pulgadas,$\angle A = 60^{\circ}$.

2. $DE = 2$pulgadas,$DF = 1$ pulgadas,$\angle D = 60^{\circ}$.

3. $AB = 2$pulgadas,$AC = 3$ pulgadas,$\angle A = 40^{\circ}$.

4. $DE = 2$pulgadas,$DF = 3$ pulgadas,$\angle D = 40^{\circ}$.

5 - 8. Nombra el ángulo incluido entre los lados

5. $AB$y$BC$ en$\triangle ABC$.

6. $XY$y$YZ$ en$\triangle XYZ$.

7. $DE$y$DF$ en$\triangle DEF$.

8. $RS$y$TS$ en$\triangle RST$.

9 - 22. Para cada una de las siguientes.

(1) enumerar dos lados y un ángulo incluido de cada triángulo que son respectivamente iguales, utilizando la información dada en el diagrama,

(2) escribir la declaración de congruencia,

(3) encontrar$x$, o$x$ y$y$.

Supongamos que los ángulos o lados marcados de la misma manera son iguales.

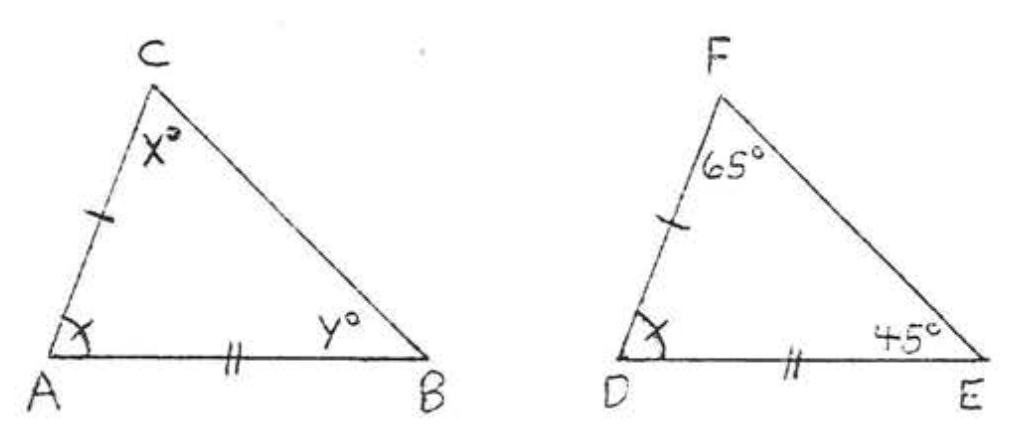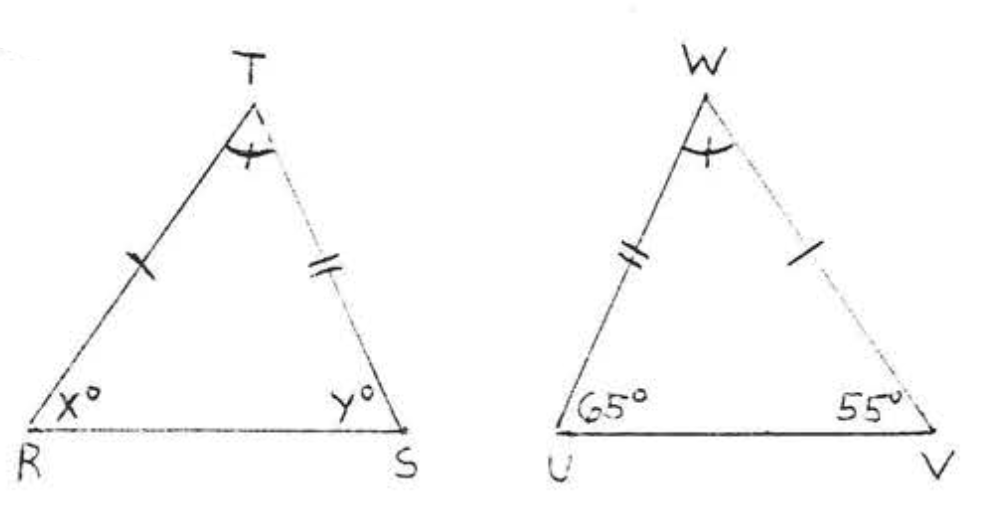
9. $Screen Shot 2020-10-30 a las 4.15.31 PM.png$ 10. $Screen Shot 2020-10-30 a las 4.15.53 PM.png$

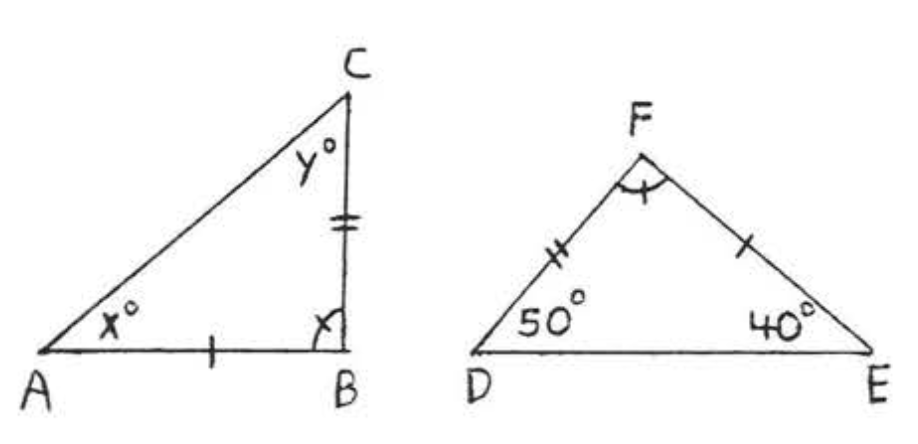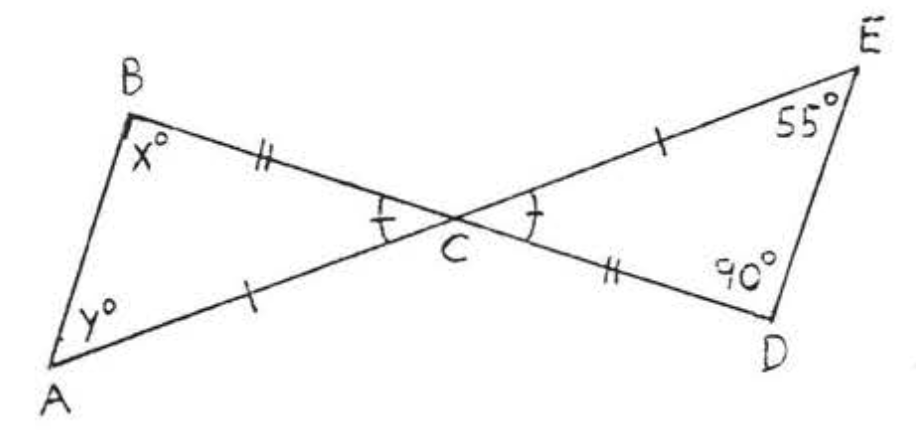
11. $Screen Shot 2020-10-30 a las 4.16.11 PM.png$ 12. $Screen Shot 2020-10-30 a las 4.16.32 PM.png$

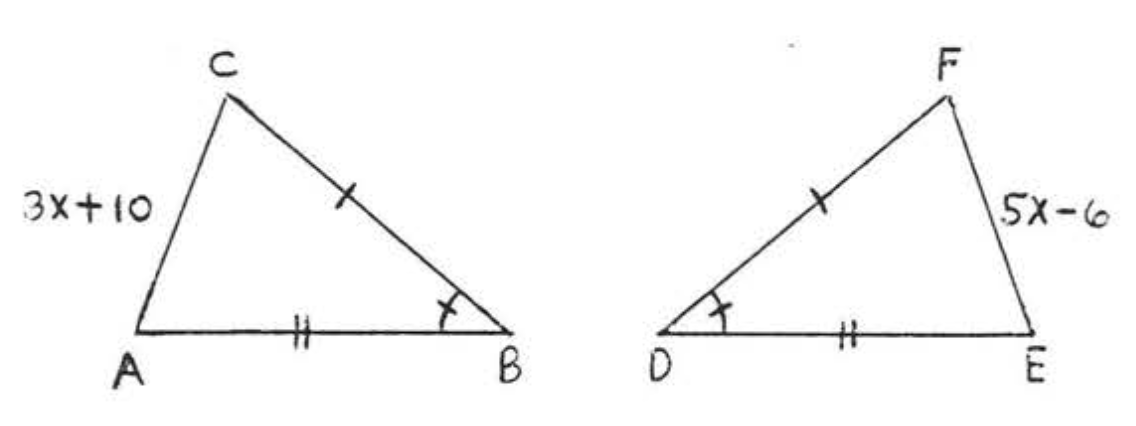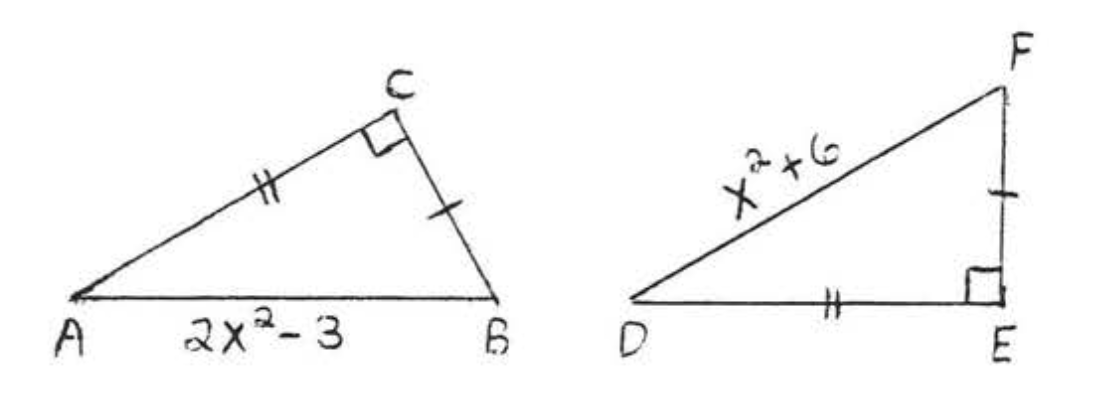
13. $Screen Shot 2020-10-30 a las 4.16.58 PM.png$ 14. $Screen Shot 2020-10-30 a las 4.17.13 PM.png$

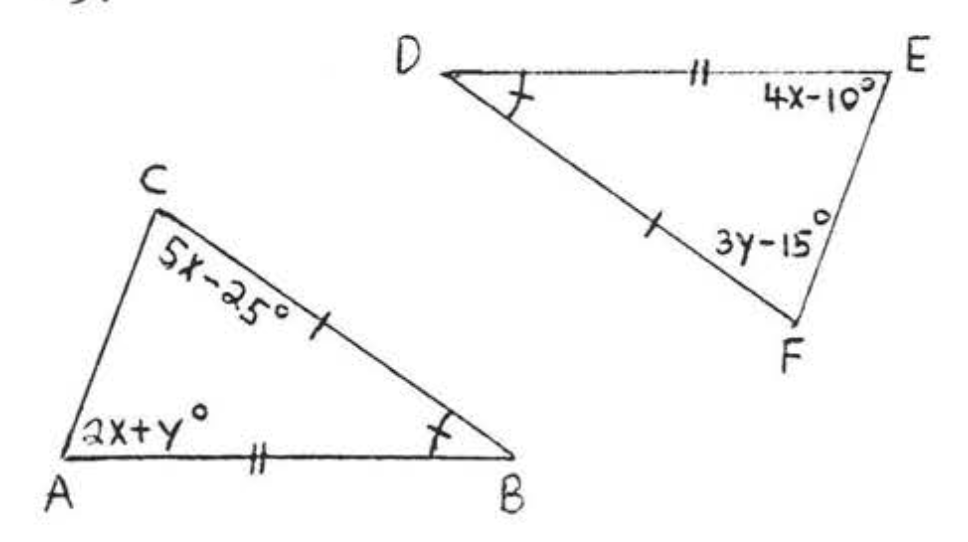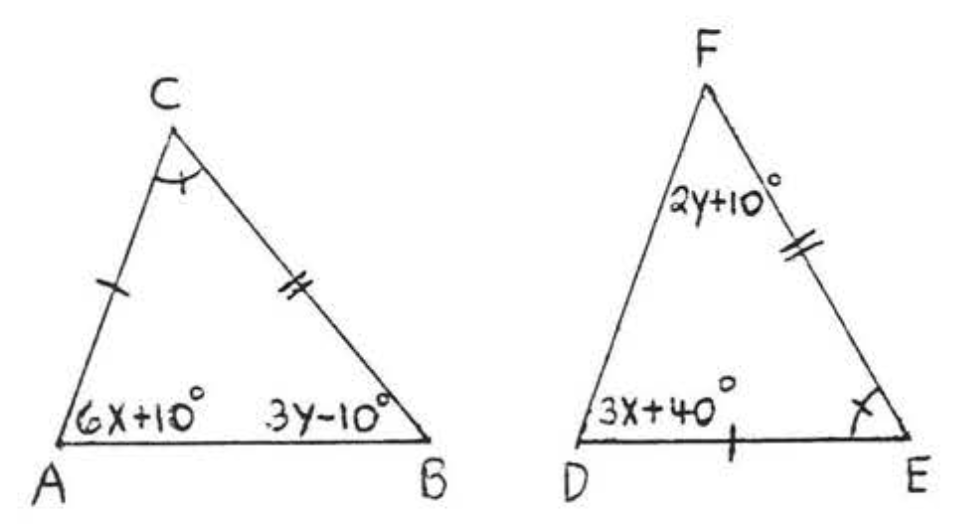
15. $Screen Shot 2020-10-30 a las 4.17.29 PM.png$ 16. $Screen Shot 2020-10-30 a las 4.17.50 PM.png$

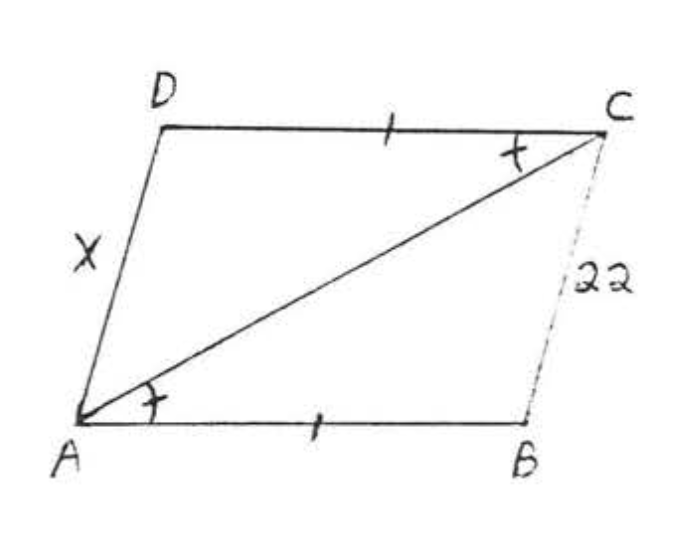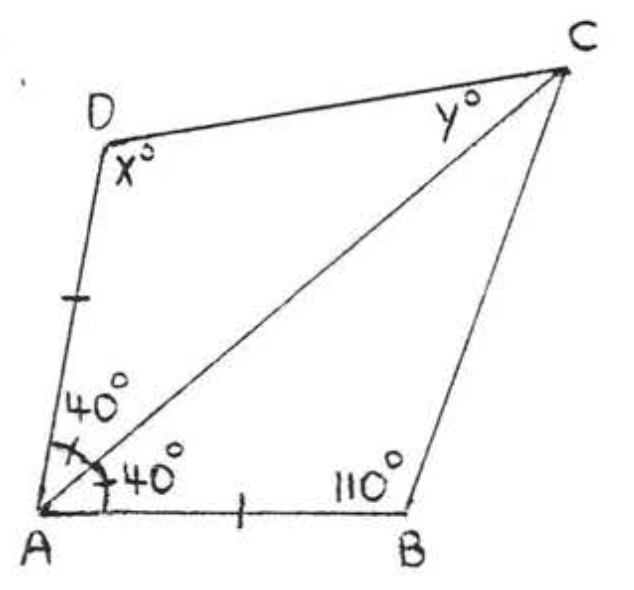
17. $Screen Shot 2020-10-30 a las 4.18.18 PM.png$ 18. $Screen Shot 2020-10-30 a las 4.18.32 PM.png$

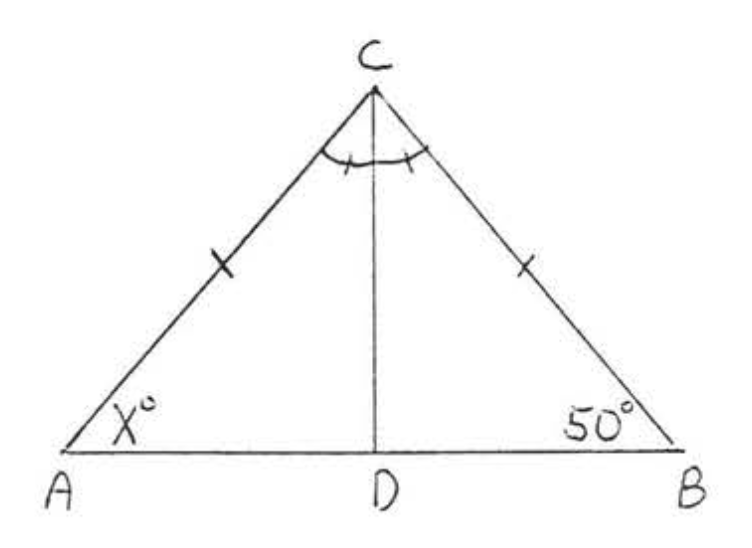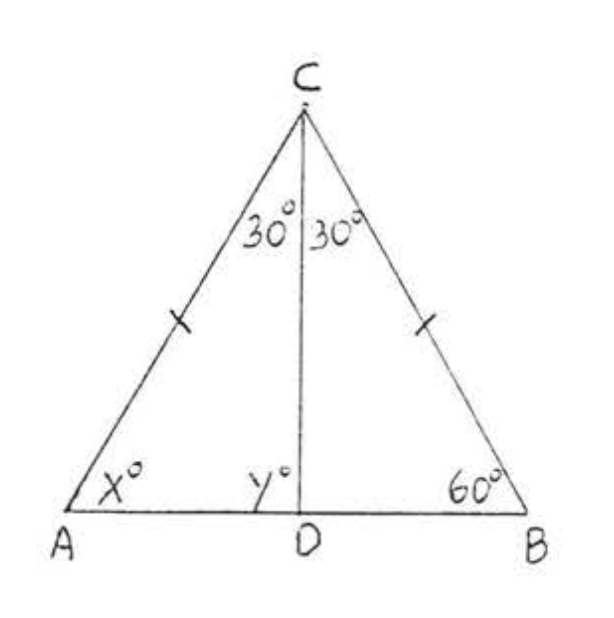
19. $Screen Shot 2020-10-30 a las 4.18.53 PM.png$ 20. $Screen Shot 2020-10-30 a las 4.19.05 PM.png$

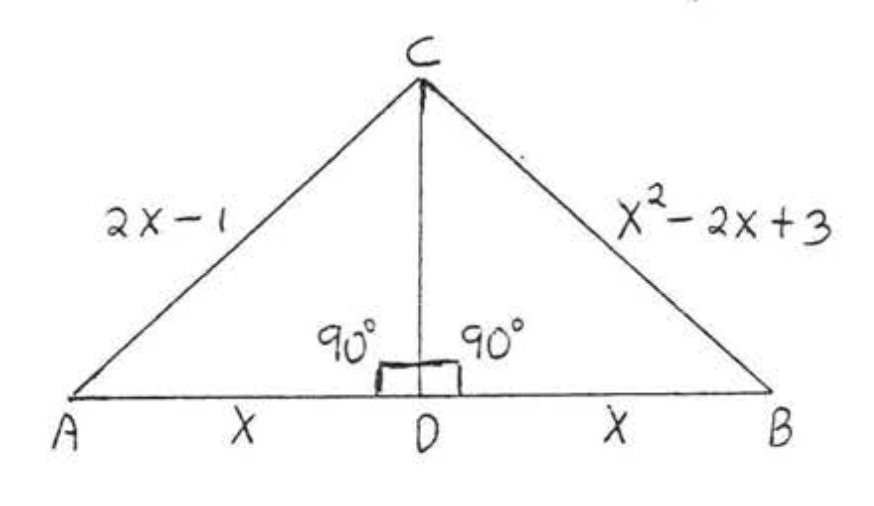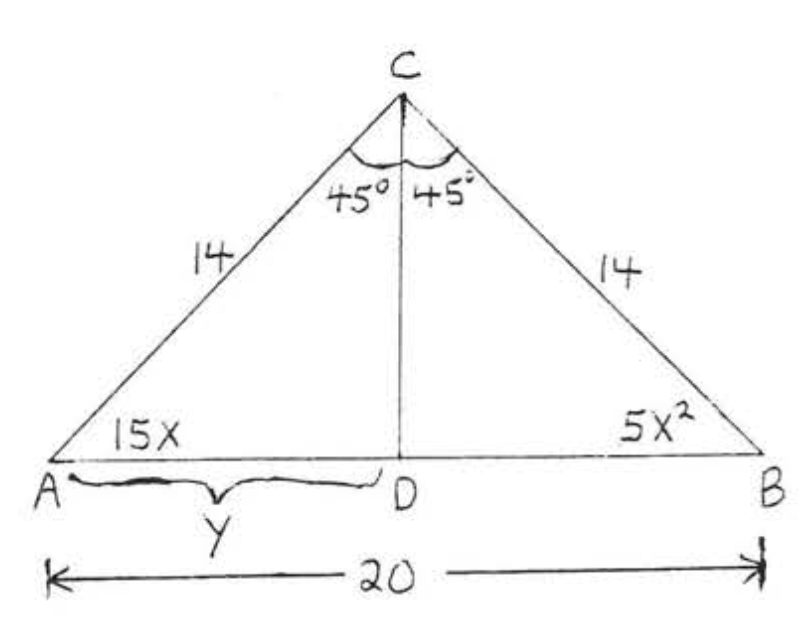
21. $Screen Shot 2020-10-30 a las 4.19.25 PM.png$ 22. $Screen Shot 2020-10-30 a las 4.19.41 PM.png$

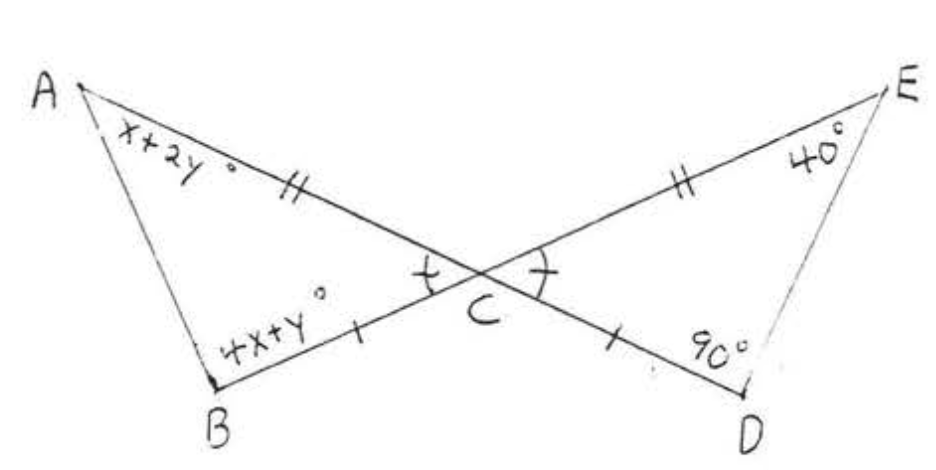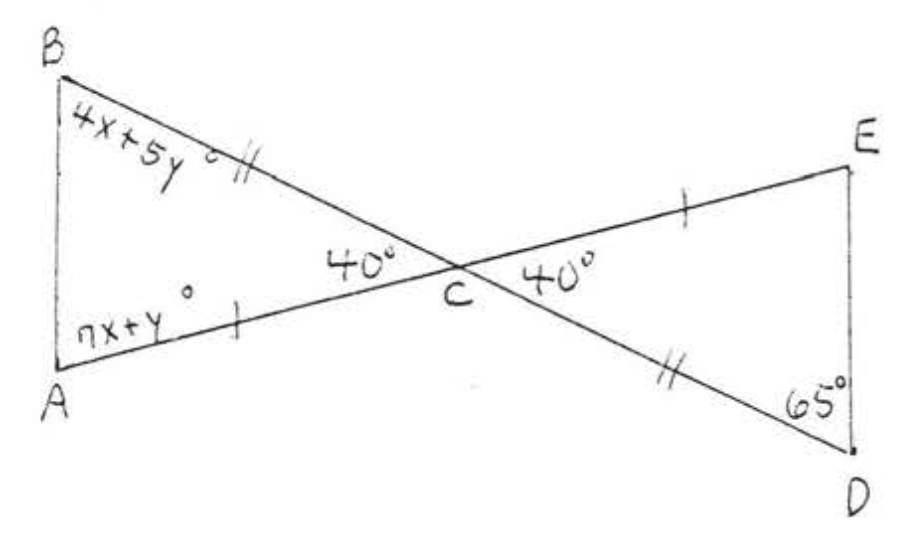
23. $Screen Shot 2020-10-30 a las 4.20.09 PM.png$ 24. $Screen Shot 2020-10-30 a las 4.20.34 PM.png$

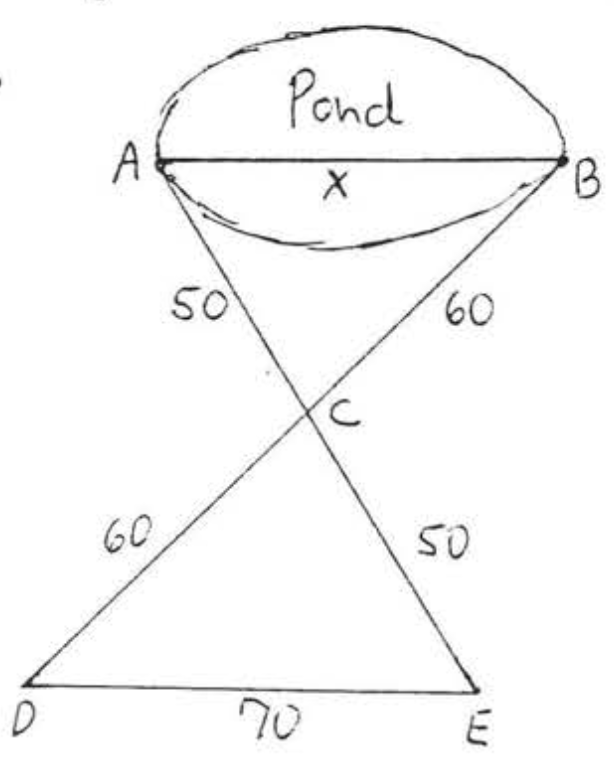25. $Screen Shot 2020-10-30 a las 4.21.03 PM.png$ 26. $Screen Shot 2020-10-30 a las 4.21.22 PM.png$

Teorema\(\PageIndex{1}\) (SAS or Side-Angle-Side Theorem)

Ejemplo\(\PageIndex{1}\)

Ejemplo\(\PageIndex{2}\)

Ejemplo\(\PageIndex{3}\)

Ejemplo\(\PageIndex{4}\)

Nota Histórica

Problemas