2.3: Los teoremas ASA y AAS
- Page ID
- 114599
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)En esta sección consideraremos dos casos más en los que es posible concluir que los triángulos son congruentes con solo información parcial sobre sus lados y ángulos,
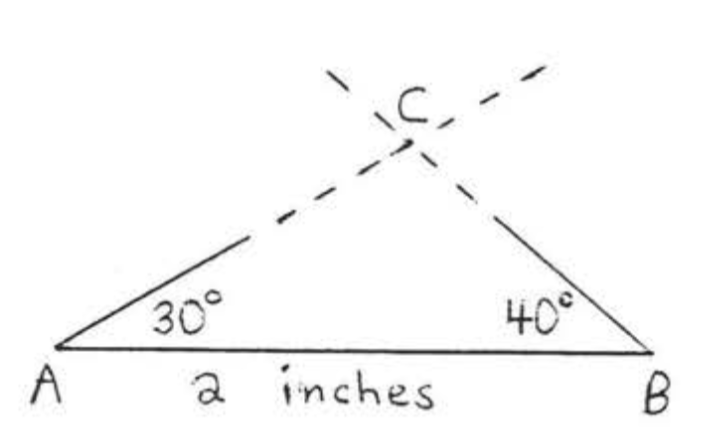
Supongamos que nos dicen que\(\triangle ABC\) tiene\(\angle A = 30^{\circ}, \angle B = 40^{\circ}\), y\(AB =\) 2 pulgadas. Intentemos bosquejar\(\triangle ABC\). Primero dibujamos un segmento de línea de 2 pulgadas y lo etiquetamos\(AB\), Con un transportador dibujamos un ángulo de\(30^{\circ}\) a\(A\) y un ángulo de\(40^{\circ}\) at\(B\) (Figura\(\PageIndex{1}\)). Extendemos las líneas formando\(\angle A\) y\(\angle B\) hasta que se encuentren en\(C\). Ahora podíamos medir\(AC, BC\), y\(\angle C\) encontrar las partes restantes del triángulo.
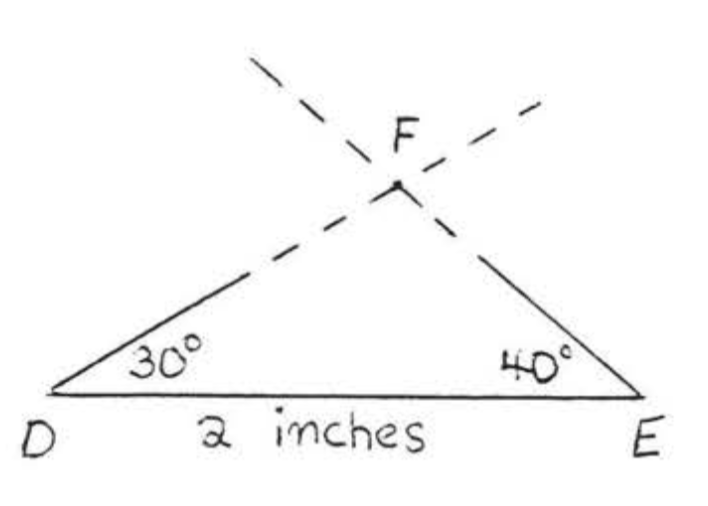
Dejar\(\triangle DEF\) ser otro triángulo, con\(\angle D = 30^{\circ}\),\(\angle E = 40^{\circ}\), y\(DE =\) 2 pulgadas. Podríamos bosquejar\(\triangle DEF\) tal como lo hicimos\(\triangle ABC\), y luego medir\(DF, EF\), y\(\angle F\) (Figura\(\PageIndex{2}\)). Es claro que debemos tener\(AC = DF\),, y\(BC = EF\)\(\angle C = \angle F\), porque ambos triángulos fueron dibujados exactamente de la misma manera, Por lo tanto\(\triangle ABC \cong \triangle DEF\).
En\(\triangle ABC\) decimos que\(AB\) es el lado incluido entre\(\angle A\) y\(\angle B\). En\(\triangle DEF\) diríamos que DE es el lado incluido entre\(\angle D\) y\(\angle E\).
Nuestra discusión sugiere el siguiente teorema:
Dos triángulos son congruentes si dos ángulos y un lado incluido de uno son iguales respectivamente a dos ángulos y un lado incluido del otro.
En la Figura\(\PageIndex{1}\) and \(\PageIndex{2}\), \(\triangle ABC \cong \triangle DEF\) because \(\angle A, \angle B\), and \(AB\) are equal respectively to \(\angle D\), \(\angle E\), and \(DE\).
A veces abreviamos Teorema\(\PageIndex{1}\) by simply writing \(ASA = ASA\).
En\(\triangle PQR\), nombre el lado incluido entre
- \(\angle P\)y\(\angle Q\).
- \(\angle P\)y\(\angle R\).
- \(\angle Q\)y\(\angle R\).
Solución
Tenga en cuenta que el lado incluido es nombrado por las dos letras que representan cada uno de los ángulos. Por lo tanto, para (1), el lado incluido entre\(\angle P\) y\(\angle Q\) es nombrado por las letras\(P\) y\(Q\) —es decir, lado\(PQ\). De manera similar para (2) y (3).
Respuesta: (1)\(PQ\), (2)\(PR\), (3)\(QR\).
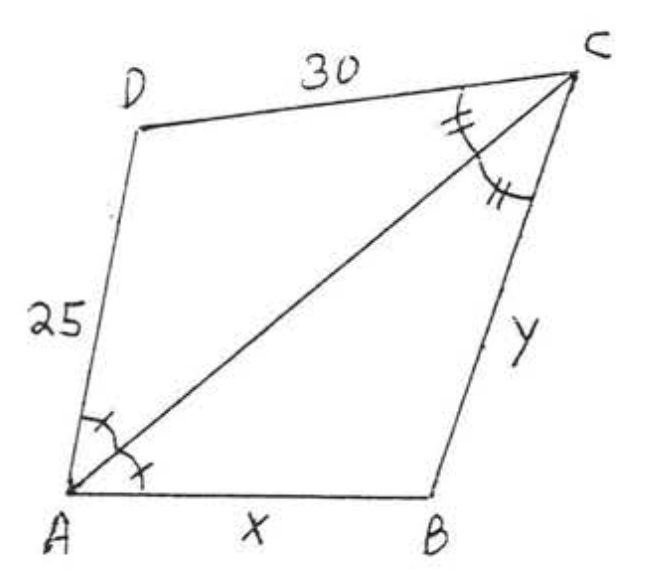
Para los dos triángulos en el diagrama
- escribir la declaración de congruencia,
- dar una razón para (1),
- encontrar\(x\) y\(y\).
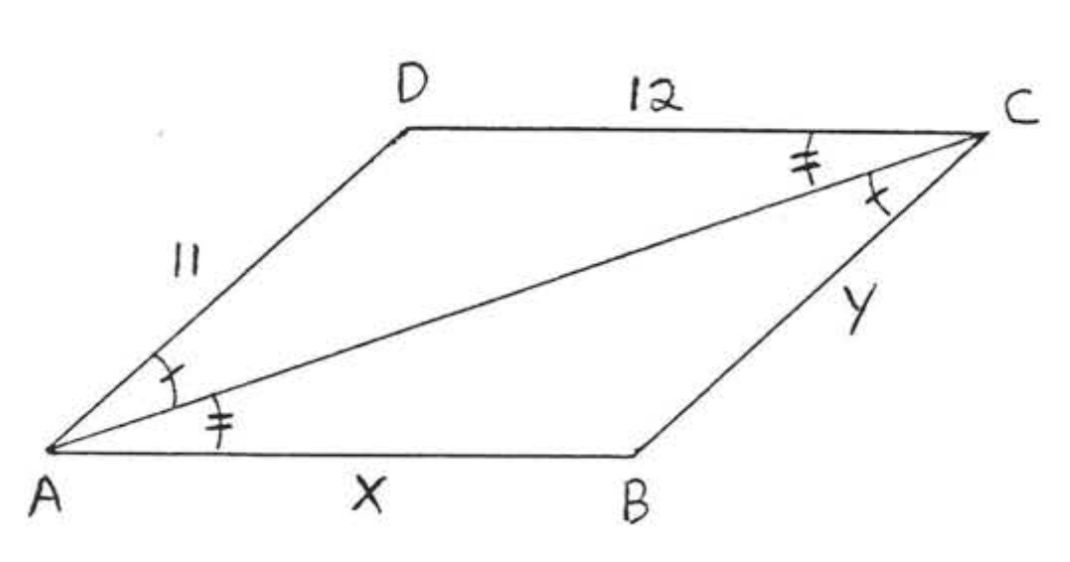
Solución
(1) Del diagrama\(\angle A\) en\(\triangle ABC\) es igual a\(\angle C\) in\(\triangle ADC\). Por lo tanto,\(A\) "" corresponde a "\(C\)”. También\(\angle C\) en\(\triangle ABC\) es igual a\(\angle A\) in\(\triangle ADC\). Entonces "\(C\)" corresponde a "\(A\)”. Tenemos
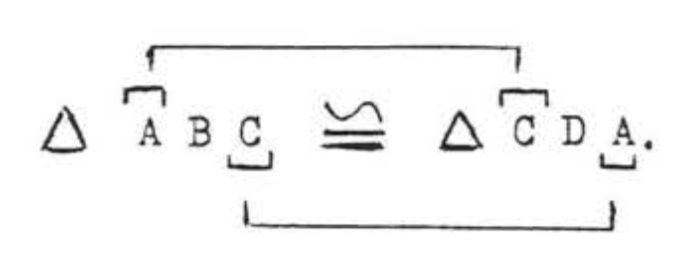
(2)\(\angle A, \angle C\), y el lado incluido\(AC\) de\(\triangle ABC\) son iguales respectivamente a\(\angle C\),\(\angle A\), y el lado incluido\(CA\) de\(\triangle CDA\). (\(AC = CA\)porque solo son nombres diferentes para el segmento de línea idéntico, a veces decimos\(AC = CA\) por identidad.) Por lo tanto\(\triangle ABC \cong \triangle CDA\) debido al Teorema ASA (\(ASA = ASA\)).
Resumen:
\(\begin{array} {ccrclcl} {} & \ & {\underline{\triangle ABC}} & \ & {\underline{\triangle CDA}} & \ & {} \\ {\text{Angle}} & \ & {\angle BAC} & = & {\angle DCA} & \ & {\text{(marked = in diagram)}} \\ {\text{Included Side}} & \ & {AC} & = & {CA} & \ & {\text{(identity)}} \\ {\text{Angle}} & \ & {\angle BCA} & = & {\angle DAC} & \ & {\text{(marked = in diagram)}} \end{array}\)
(3)\(AB = CD\) y\(BC = DA\) porque son lados correspondientes de los triángulos congruentes. Por lo tanto\(x = AB = CD = 12\) y\(y = BC = DA = 11\).
Respuesta:
(1)\(\triangle ABC \cong \triangle CDA\).
(2). \(ASA = ASA\):\(\angle A, AC, \angle C\) de\(\triangle ABC = \angle C\),\(CA\),\(\angle A\) de\(\triangle CDA\).
(3)\(x = 12\),\(y = 11\).
Consideremos ahora\(\triangle ABC\) y\(\triangle DEF\) en Figura\(\PageIndex{3}\). \(\angle A\) and \(\angle B\)
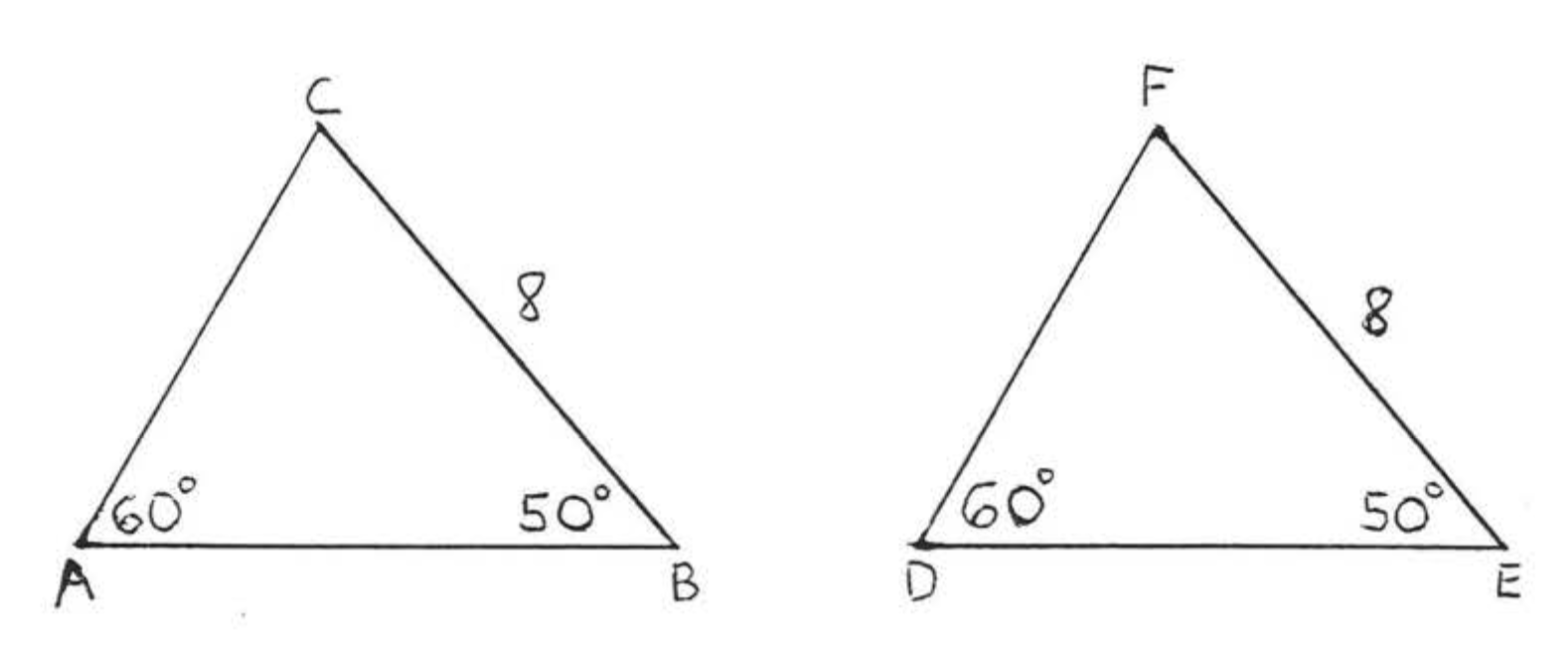
de\(\triangle ABC\) son iguales respectivamente a\(\angle D\) y\(\angle E\) de\(\triangle DEF\), sin embargo no tenemos información sobre los lados incluidos entre estos ángulos,\(AB\) y\(DE\), En cambio sabemos que el lado inincluido BC es igual al lado no incluido correspondiente\(EF\). Por lo tanto, tal como están las cosas, no podemos usar\(ASA = ASA\) para concluir que los triángulos son congruentes, Sin embargo podemos mostrar\(\angle C\) iguales\(\angle F\) como en el Teorema\(\PageIndex{3}\), section 1.5 \((\angle C = 180^{\circ} - (60^{\circ} + 50^{\circ}) = 180^{\circ} - 110^{\circ} = 70^{\circ}\) and \(\angle F = 180^{\circ} - (60^{\circ} + 50^{\circ}) = 180^{\circ} - 110^{\circ} = 70^{\circ})\). Entonces podemos aplicar el Teorema ASA a los ángulos Banda\(C\) y su lado incluido\(BC\) y el correspondiente ángulos\(E\) y\(F\) con lado EF incluido. Estas observaciones nos llevan al siguiente teorema:
Dos triángulos son congruentes si dos ángulos y un lado no incluido de un triángulo son iguales respectivamente a dos ángulos y el lado no incluido correspondiente del otro triángulo (\(AAS = AAS\)).
En la Figura\(\PageIndex{4}\), if \(\angle A = \angle D\), \(\angle B = \angle E\) and \(BC = EF\) then \(\triangle ABC \cong \triangle DEF\).
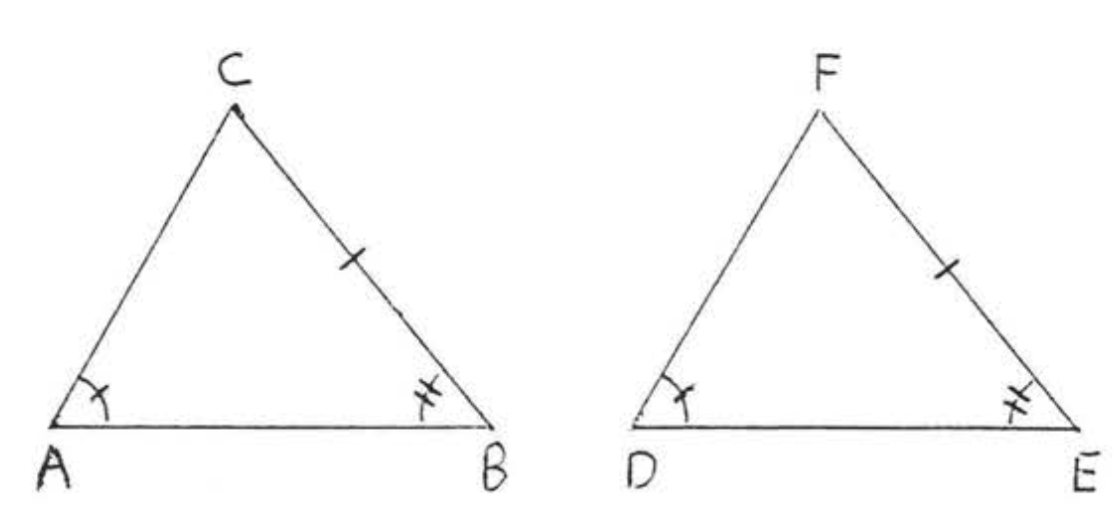
- Prueba
-
\(\angle C = 180^{\circ} - (\angle A + \angle B) = 180^{\circ} - (\angle D + \angle E) = \angle F\). Los triángulos son entonces congruentes al\(ASA = ASA\) aplicarse a\(\angle B\). \(\angle C\)y\(BC\) de\(\angle ABC\) y\(\angle E, \angle F\) y\(EF\) de\(\triangle DEF\).
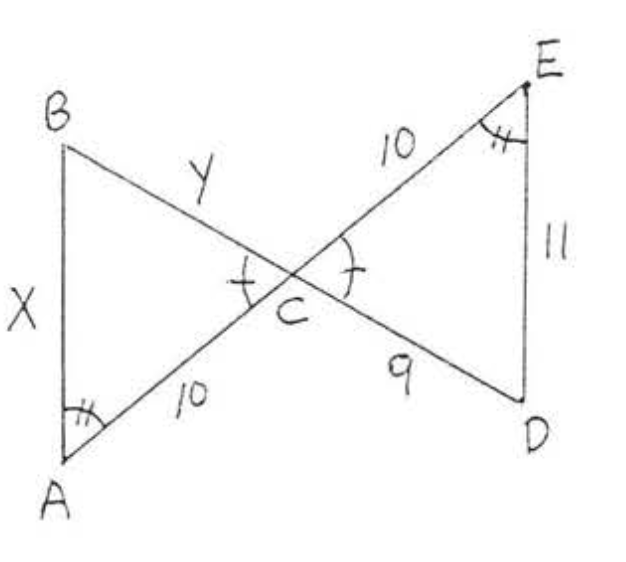
Para dos triángulos en el diagrama
- escribir la declaración de congruencia,
- dar una razón para (1),
- encontrar\(x\) y\(y\).
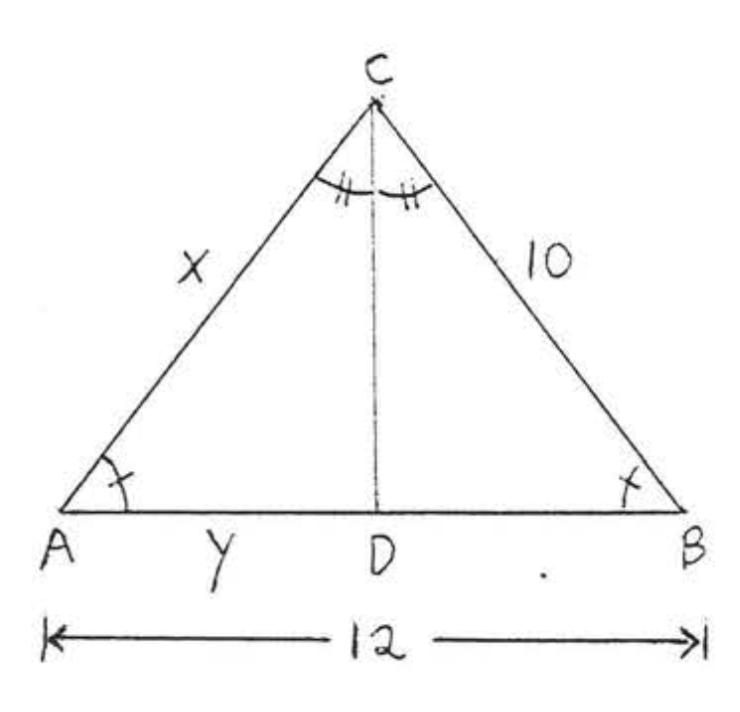
Solución
(1)\(\triangle ACD \cong \triangle BCD\).
(2)\(AAS = AAS\) ya que\(\angle A, \angle C\) y el lado no incluido\(CD\) de\(\angle ACD\) son iguales respectivamente a\(\angle B, \angle C\) y el lado no incluido\(CD\) de\(\triangle BCD\).
\(\begin{array} {ccrclcl} {} & \ & {\underline{\triangle ACD}} & \ & {\underline{\triangle BCD}} & \ & {} \\ {\text{Angle}} & \ & {\angle A} & = & {\angle B} & \ & {\text{(marked = in diagram)}} \\ {\text{Angle}} & \ & {\angle ACD} & = & {\angle BCD} & \ & {\text{(marked = in diagram)}} \\ {\text{Unincluded Side}} & \ & {CD} & = & {CD} & \ & {\text{(identity)}} \end{array}\)
(3)\(AC = BC\) y\(AD = BD\) ya que son lados correspondientes de los triángulos congruentes. Por lo tanto\(x = AC = BC = 10\) y\(y = AD = BD\). Ya que\(AB = AD + BD = y + y = 2y = 12\), debemos tener\(y = 6\).
Responder
(1)\(\triangle ACD \cong \triangle BCD\)
(2)\(AAS = AAS\):\(\angle A, \angle C, CD\)\(\triangle ACD = \angle B, \angle C, CD\) de\(\triangle BCD\).
(3)\(x = 10\),\(y = 6\).
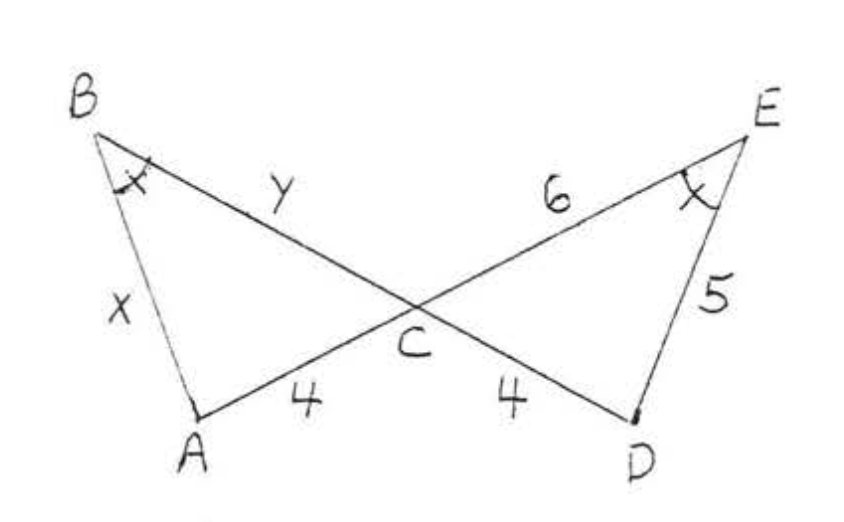
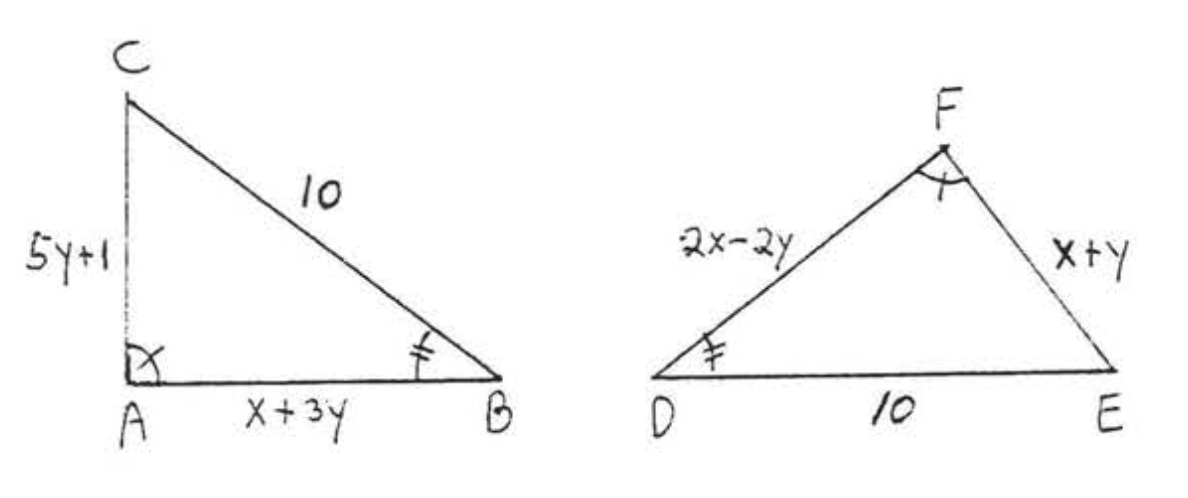
Para los dos triángulos en el diagrama
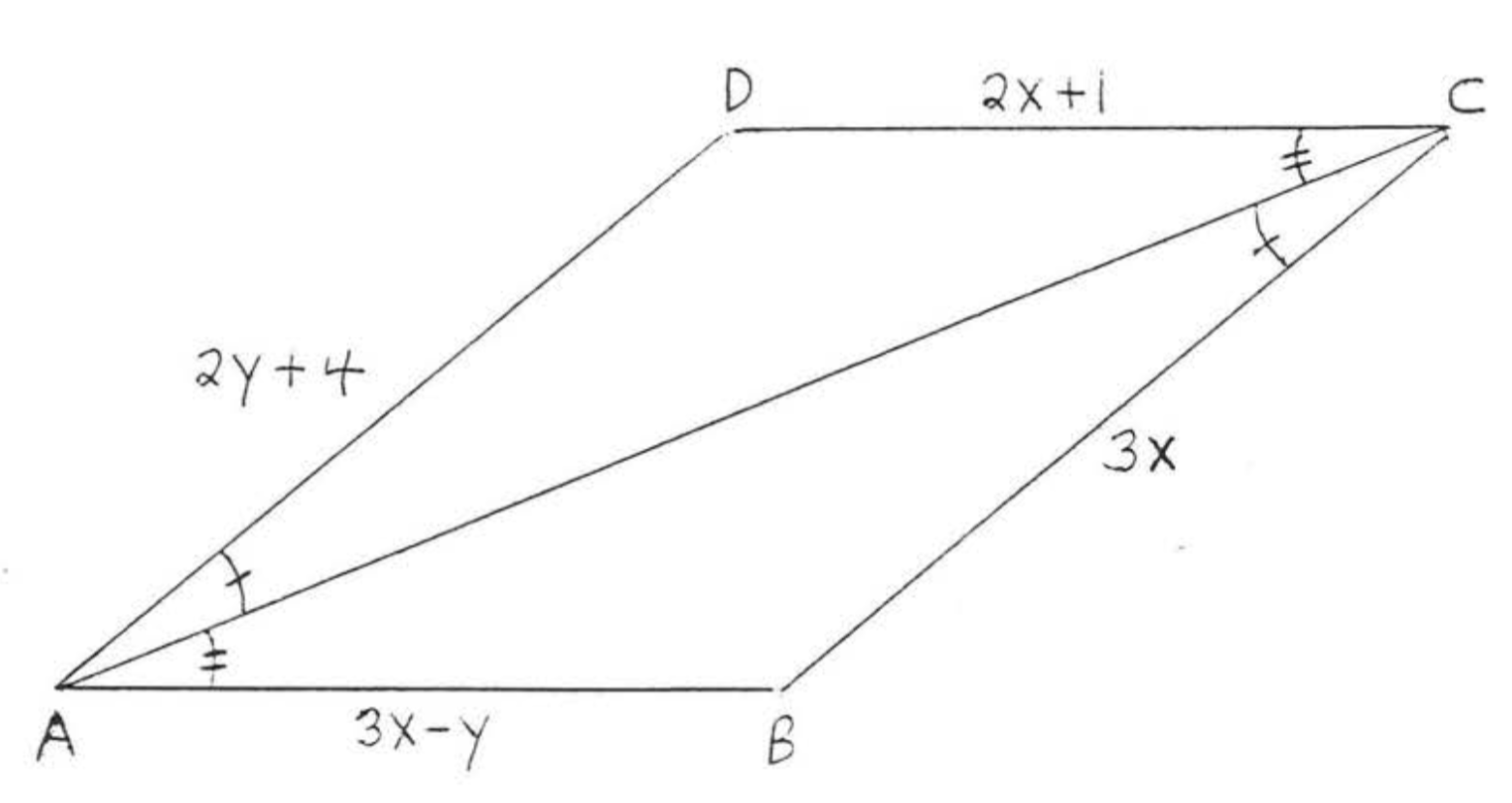
- escribir la declaración de congruencia,
- dar una razón para (1),
- encontrar\(x\) y\(y\).
Solución
La parte (1) y la parte (2) son idénticas a Ejemplo\(\PageIndex{2}\).
(3):
\(\begin{array} {rcl} {AB} & = & {CD} \\ {3x - y} & = & {2x + 1} \\ {3x - 2x - y} & = & {1} \\ {x - y} & = & {1} \end{array}\)y\(\begin{array} {rcl} {BC} & = & {DA} \\ {3x} & = & {2y + 4} \\ {3x - 2y} & = & {4} \end{array}\)
Resolvemos estas ecuaciones simultáneamente para\(x\) y\(y\):
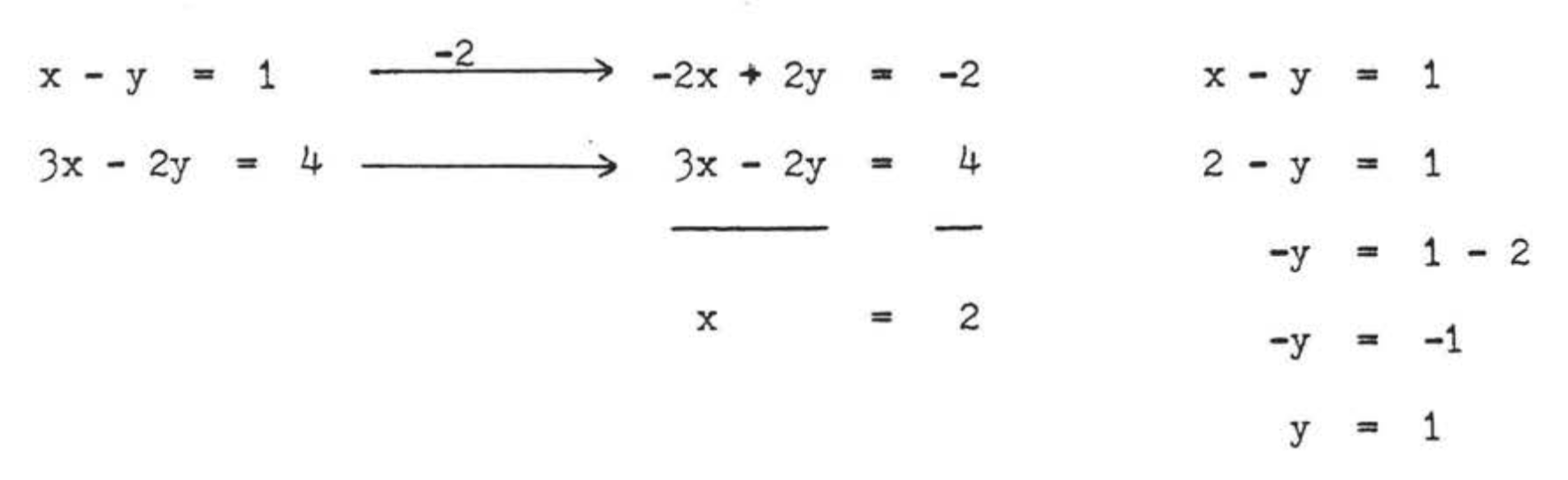
Comprobar:

Respuesta:
(1) y (2) igual que Ejemplo\(\PageIndex{2}\).
(3)\(x = 2\),\(y = 1\).
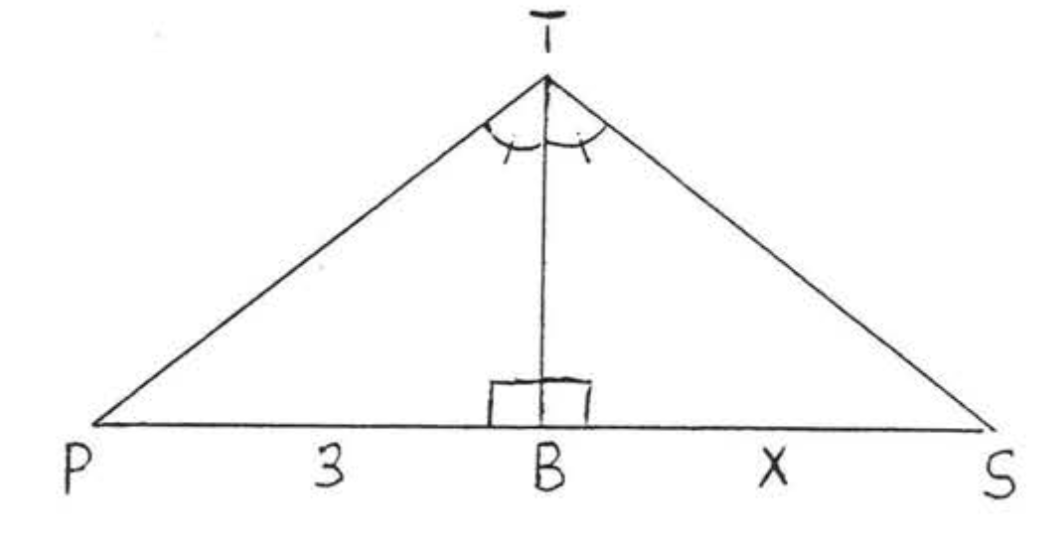
Desde lo alto de una torre Ton the shore, un barco Sis avistado en el mar, También se avistó desde un punto\(P\) a lo largo de la costa\(T\) para que\(\angle PTB = \angle STB\). Si la distancia desde\(P\) la base de la torre\(B\) es de 3 millas, ¿a qué distancia está el barco del punto Bon the shore?
Solución
\(\triangle PTB \cong \triangle STB\)por\(ASA = ASA\). Por lo tanto\(x = SB = FB = 3\).
Respuesta: 3 miles
El método de búsqueda de la distancia de barcos en el mar descrito en Ejemplo\(\PageIndex{5}\) ha sido atribuido al filósofo griego Thales (c. 600 a.C.). Sabemos por diversos autores que el Teorema ASA se ha utilizado para medir distancias desde la antigüedad, Hay una historia que uno de los oficiales de Napoleón utilizó el Teorema ASA para medir el ancho de un río que su ejército tuvo que cruzar, (ver Problema 25 más abajo.)
Problemas
1 - 4. Para cada uno de los siguientes (1) dibujar el triángulo con los dos ángulos y el lado incluido y (2) medir los lados restantes y el ángulo,
1. \(\triangle ABC\)con\(\angle A = 40^{\circ}\),\(\angle B = 50^{\circ}\), y\(AB = 3\) pulgadas,
2. \(\triangle DEF\)con\(\angle D = 40^{\circ}\),\(\angle E = 50^{\circ}\), y\(DE = 3\) pulgadas,
3. \(\triangle ABC\)con\(\angle A = 50^{\circ}\),\(\angle B = 40^{\circ}\), y\(AB = 3\) pulgadas,
4. \(\triangle DEF\)con\(\angle D = 50^{\circ}\),\(\angle E = 40^{\circ}\), y\(DE = 3\) pulgadas.
5 - 8. Nombra el lado incluido entre los ángulos:
5. \(\angle A\)y\(\angle B\) en\(\triangle ABC\).
6. \(\angle X\)y\(\angle Y\) en\(\triangle XYZ\).
7. \(\angle D\)y\(\angle F\) en\(\triangle DEF\).
8. \(\angle S\)y\(\angle T\) en\(\triangle RST\).
9 - 22. Para cada una de las siguientes
(1) escribir una declaración de congruencia para los dos triángulos,
(2) dar una razón para (1) (Teoremas SAS, ASA o AAS),
(3) encontrar\(x\), o\(x\) y\(y\).
9. 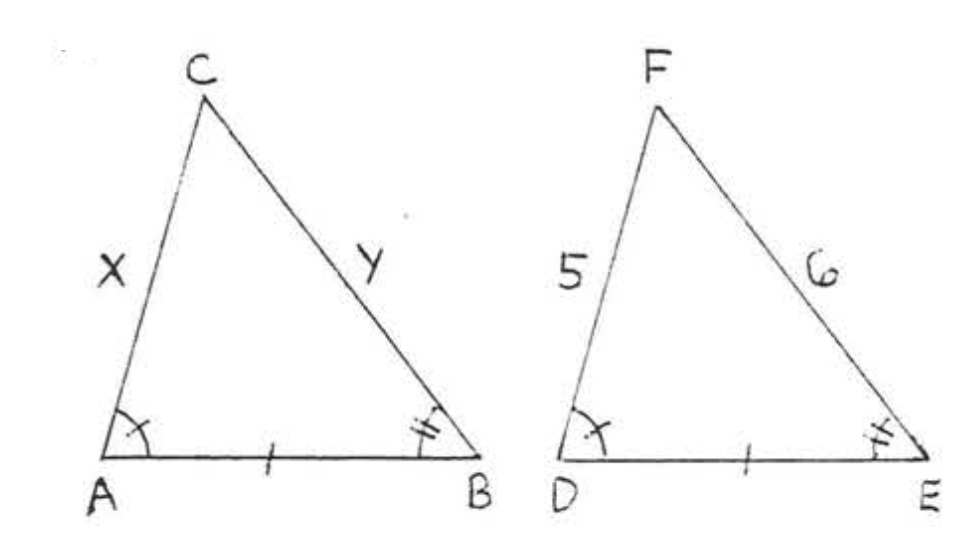 10.
10. 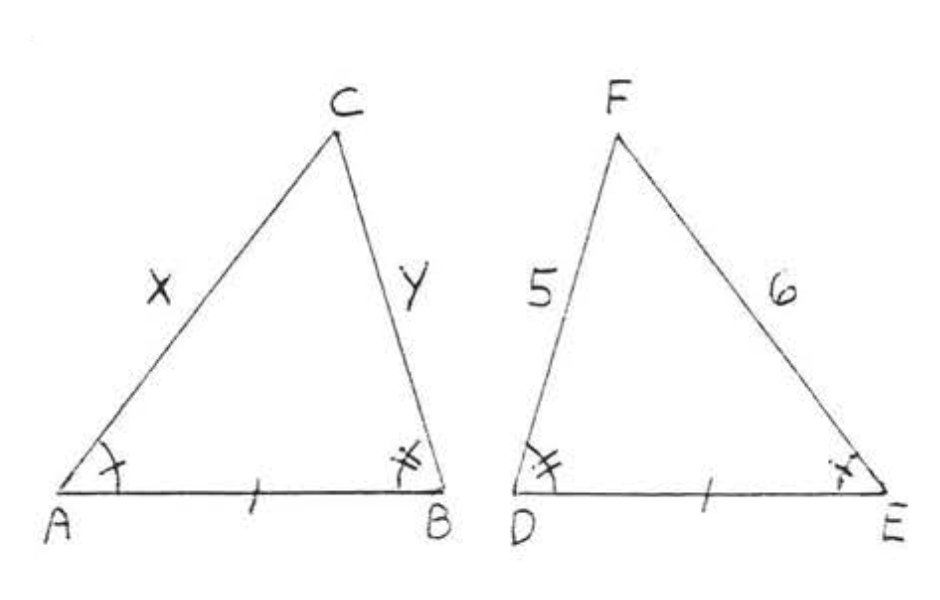
11. 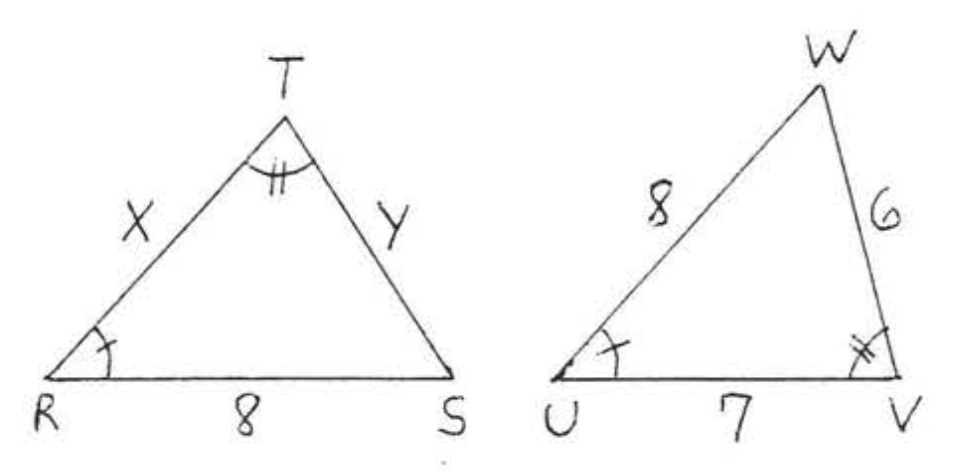 12.
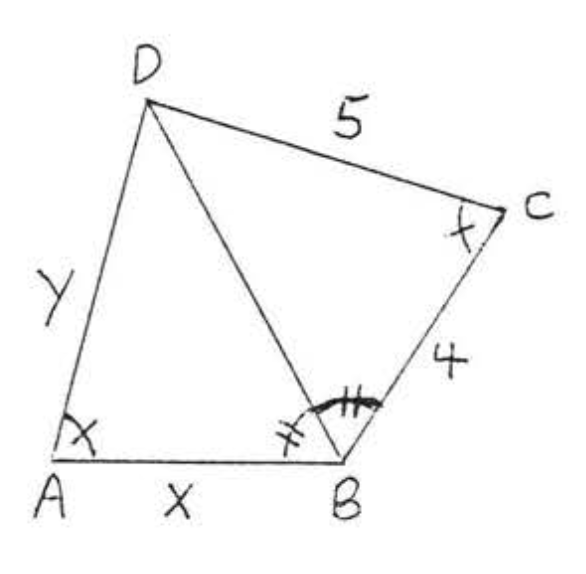
12. 
13. 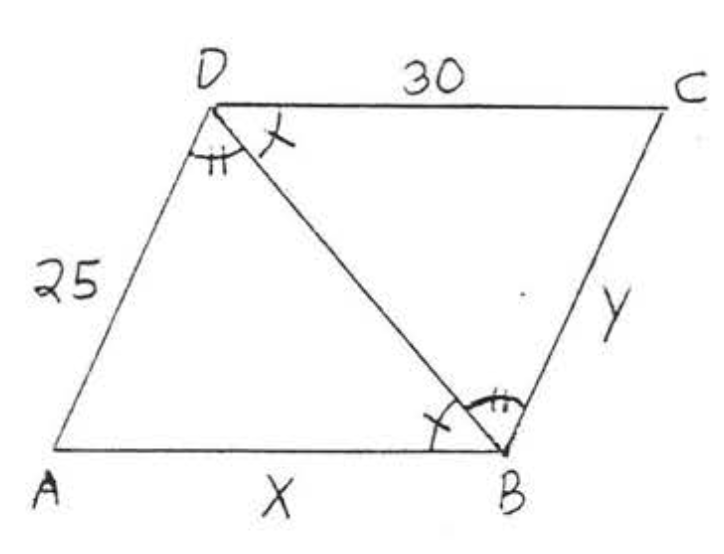 14.
14. 
15.  16.
16. 
17.  18.
18. 
19. 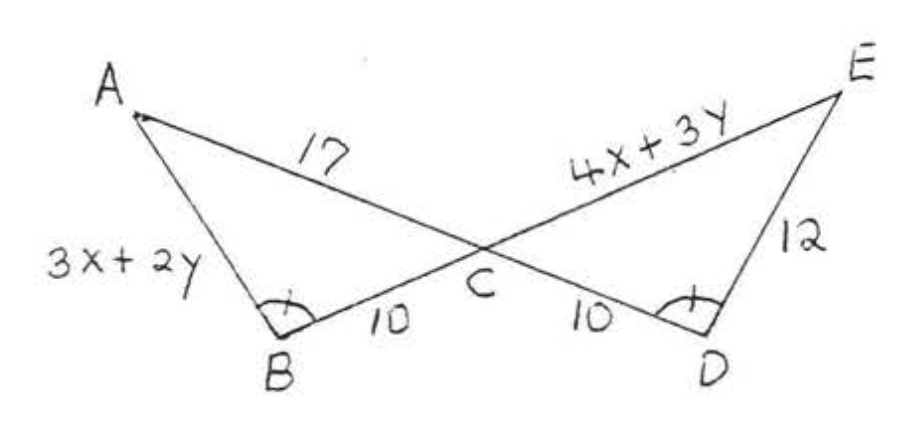 20.
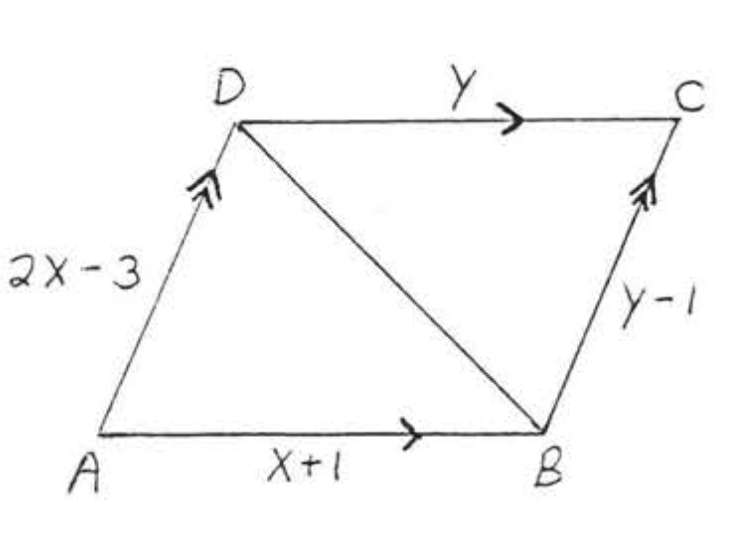
20. 
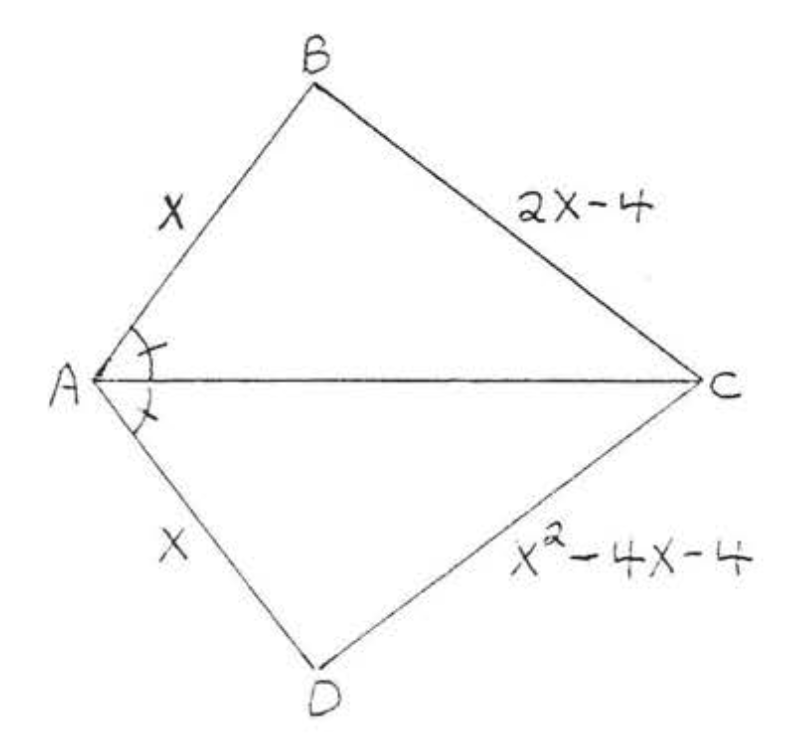
21. 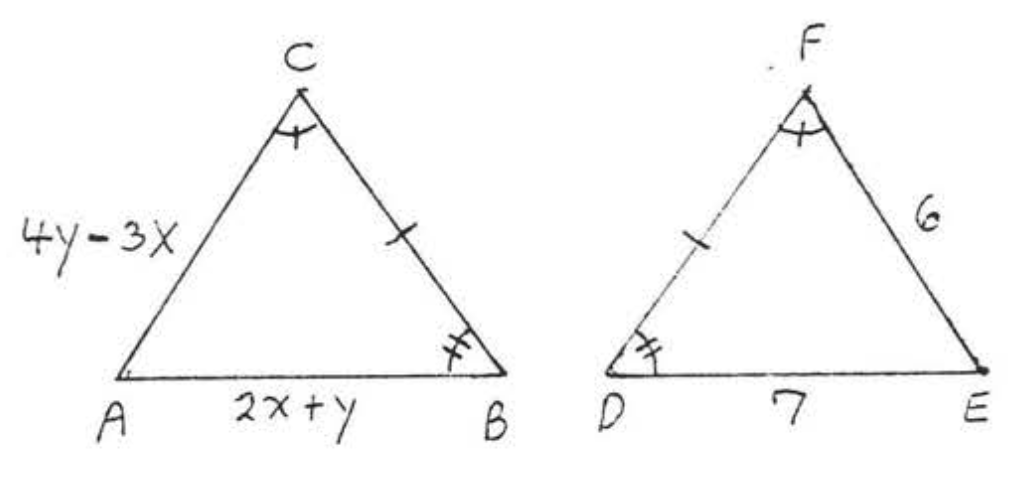 22.
22. 
23 - 26. Para cada una de las siguientes, incluya la declaración de congruencia y el motivo como parte de su respuesta:
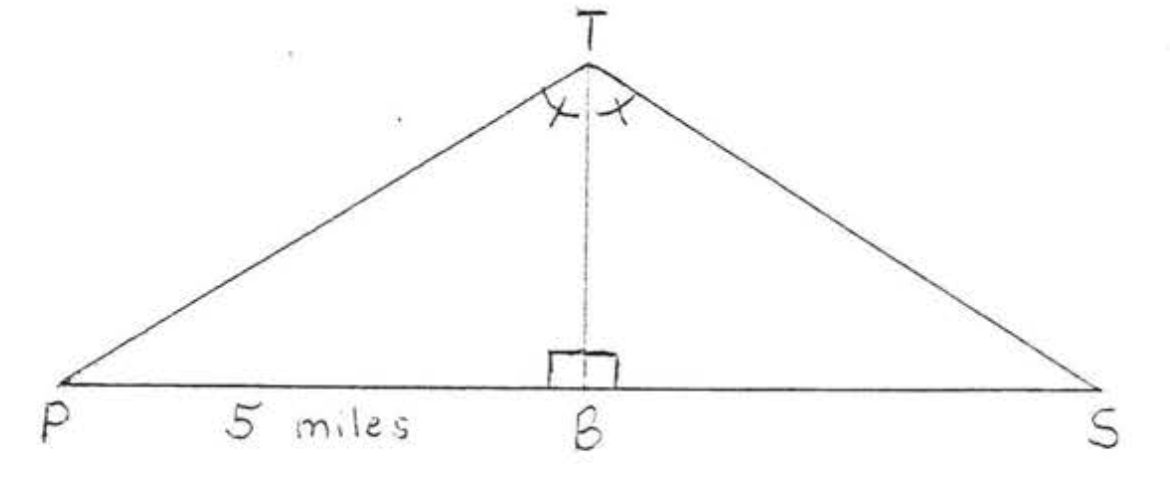
23. En el diagrama ¿a qué distancia está el barco S del punto\(P\) en la costa?
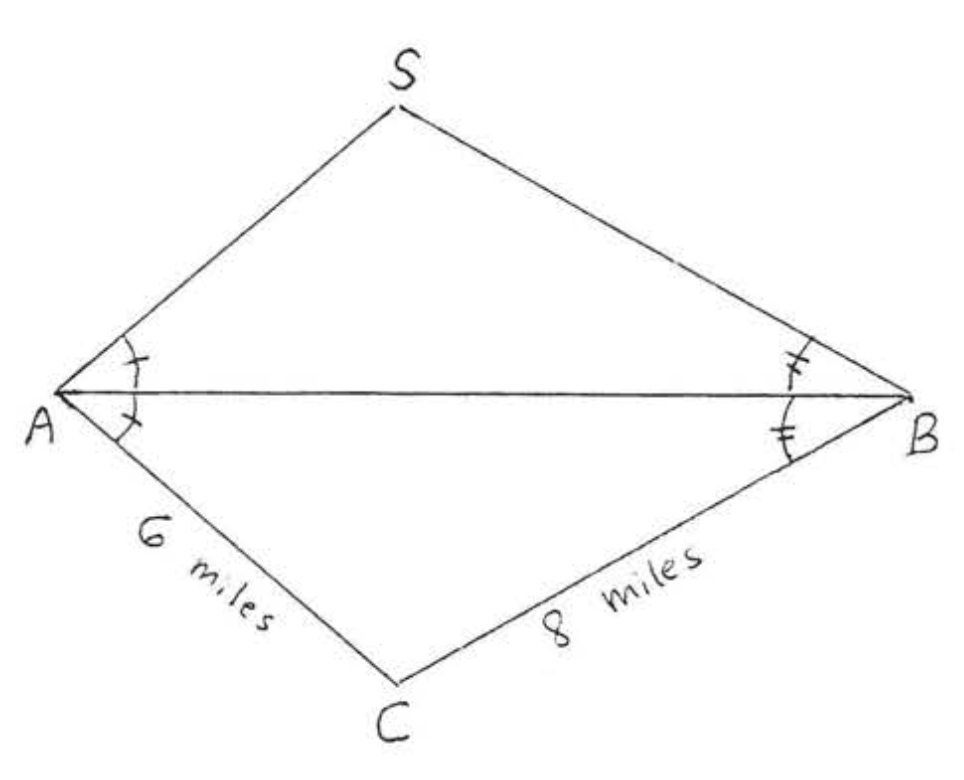
24. \(S\)El barco se observa desde puntos\(A\) y\(B\) a lo largo de la costa. Luego\(ABC\) se construye el triángulo y se mide como en el diagrama, ¿Qué tan lejos está el barco del punto\(A\)?
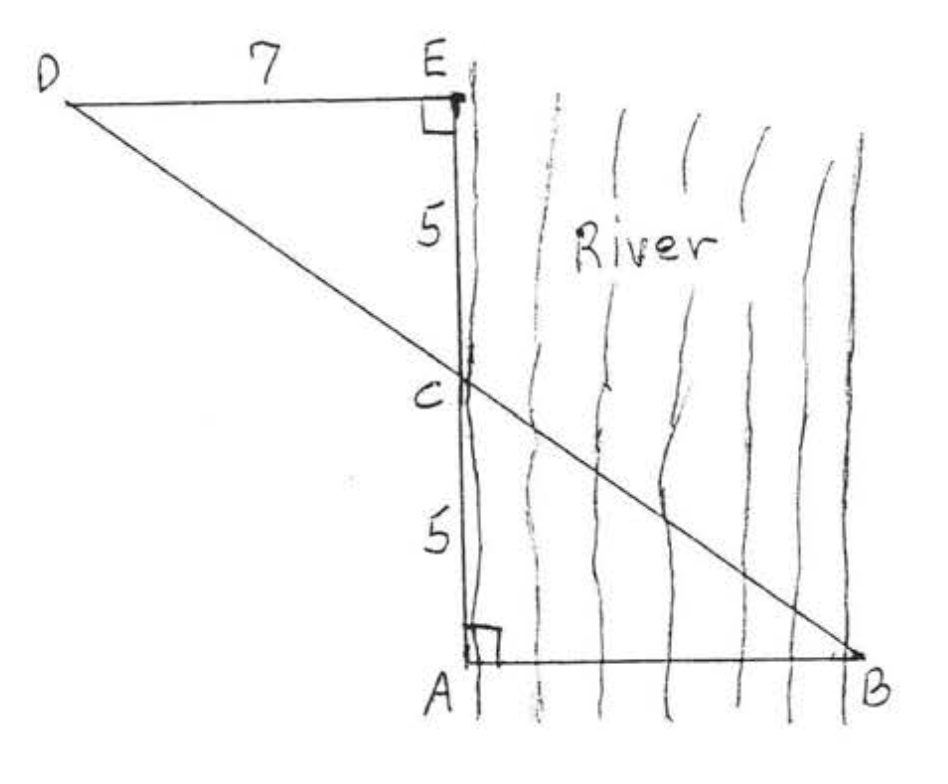
25. Encuentra la distancia\(AB\) a través de un río si\(AC = CD = 5\) y\(DE = 7\) como en el diagrama.
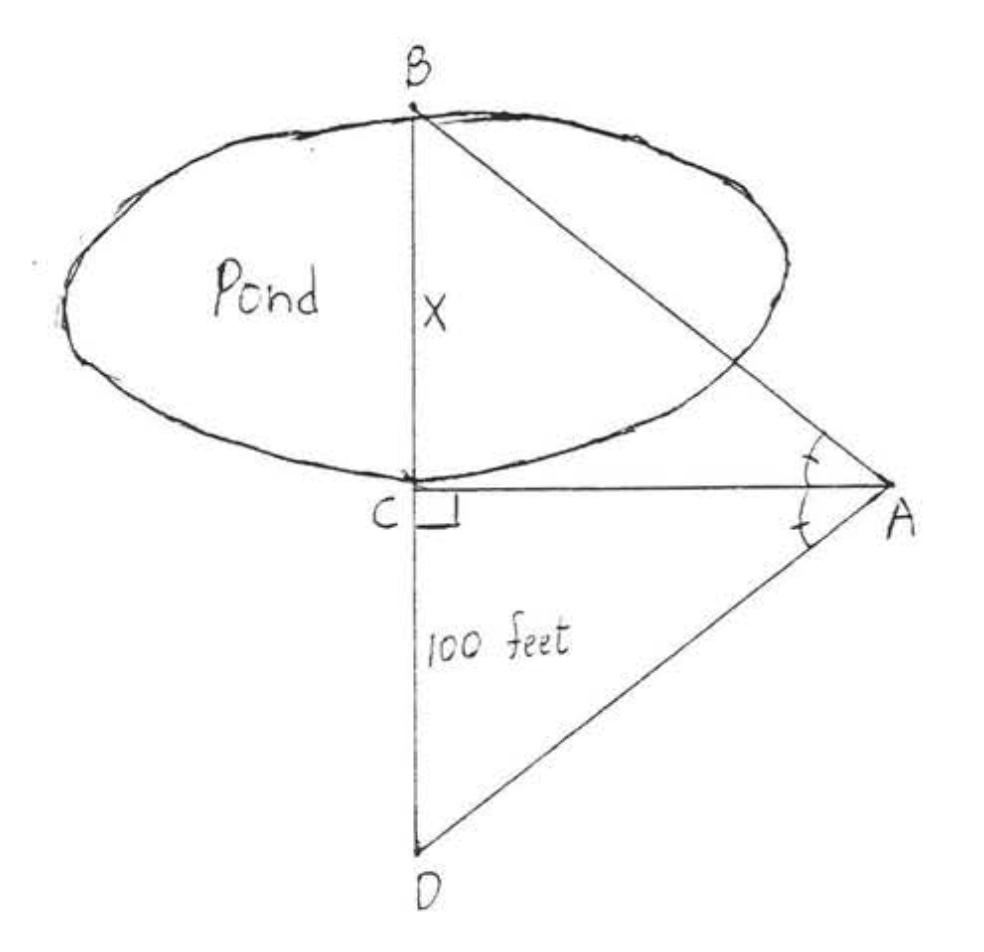
26. esa es la distancia a través del estanque?