2.4: Probar líneas y ángulos iguales

Última actualización
Guardar como PDF

Page ID: 114616

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Podemos probar líneas y ángulos iguales si podemos mostrar que son partes correspondientes de triángulos congruentes, Nos parece conveniente presentar estas pruebas en forma de doble columna con declaraciones en la columna izquierda y el motivo de cada enunciado a la derecha.

Ejemplo$\PageIndex{1}$

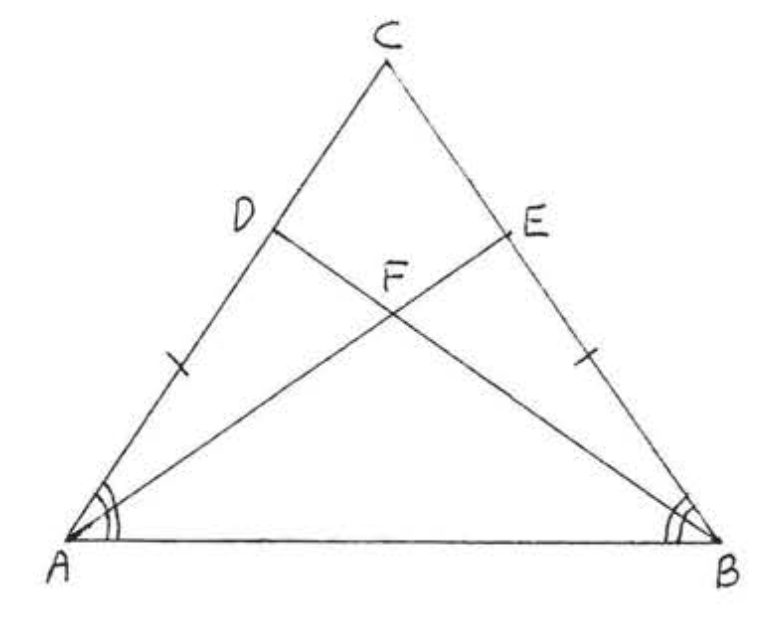
Dado$AB || CD$ y$AB = CD$ probar$AD = BC$

$2020-10-30 5.50.12.png$

Solución

Declaraciones	Razones
1. $AB = CD$.	1. Dado.
2. $\angle ABD = \angle CDB$.	2. Los ángulos interiores alternos de las líneas paralelas$(AB \|\| CD)$ son iguales.
3. $BD = DB$.	3. Identidad.
4. $\triangle ABD \cong \triangle CDB$	4. $SAS = SAS$:$AB, \angle B, BD$ de$\triangle ABD = CD$,$\angle D$,$DB$ de$\triangle CDB$.
5. $AD = BC$	5. Los lados correspondientes de los triángulos congruentes son iguales,

Explicación: Cada una de las tres primeras declaraciones dice que un lado o ángulo de$\triangle ABD$ es igual al lado o ángulo correspondiente de$\triangle CDB$, Para llegar a estas declaraciones, primero debemos escribir la declaración de congruencia utilizando los métodos de las secciones anteriores. Luego seleccionamos tres pares de lados o ángulos correspondientes que son iguales por una de las siguientes razones:

Razones Las Líneas Son Iguales

Dado. Esto significa que se nos pide que asumamos que las líneas son iguales al inicio del ejercicio, Por ejemplo, el problema va a indicar “dado$AB = CD$" o$AB$ y se$CD$ marcará de la misma manera en el diagrama.
Identidad. Esto significa que el segmento de línea idéntico aparece en ambos triángulos, Por ejemplo,$BD$ y$DB$ representan el mismo segmento de línea, Por supuesto que la longitud de un segmento de línea es igual a sí mismo.

Razones Los Ángulos Son Iguales

Dado.
Identidad.
Los ángulos interiores alternos de las líneas paralelas son iguales. Para aplicar esta razón hay que dar que las líneas son paralelas.
Ángulos correspondientes de líneas paralelas iguales.
Los ángulos verticales son iguales.

Estas no son las únicas razones posibles sino que son todas las que usaremos al principio.

También debemos seleccionar los tres pares de lados o ángulos iguales para que una de las razones$SAS = SAS$,$ASA = ASA$, o$AAS = AAS$ pueda ser utilizada para justificar la declaración de congruencia en el enunciado 4, En las secciones 2.6 y 2.7, daremos algunas razones adicionales para que dos triángulos sean congruentes.

El enunciado 5 es el que deseamos probar, La razón es que los lados (o ángulos) correspondientes de triángulos congruentes son iguales. Wecan usar esta razón aquí porque los triángulos ya han sido comprobados congruentes en el comunicado 4,

Un comentario final, Observe cómo la solución de Ejemplo se$\PageIndex{1}$ conforma con nuestra definición original de prueba, Cada nueva declaración se muestra como verdadera mediante el uso de declaraciones y razones anteriores que ya se han establecido.

Demos otro ejemplo:

Ejemplo$\PageIndex{2}$

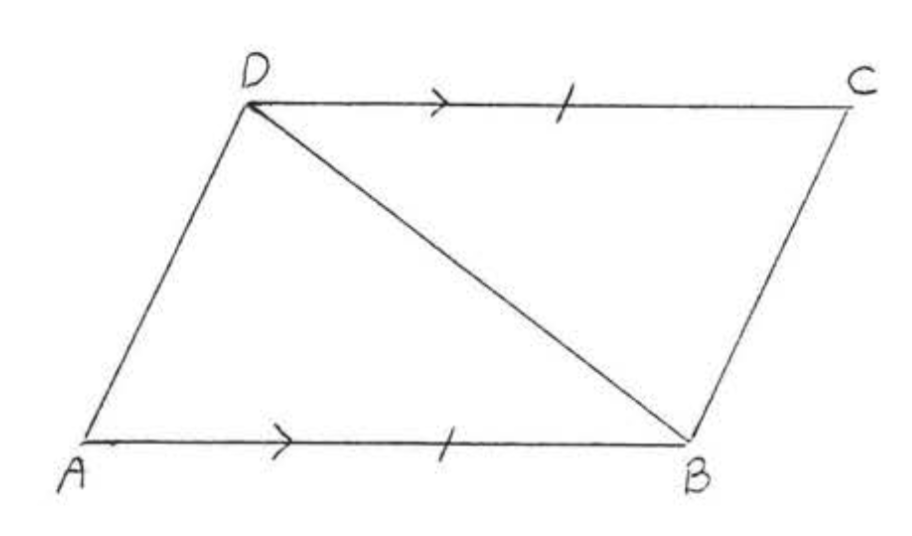
Dado$QP || ST$ y$QR = TR$ probar$PR = SR$.

$2020-10-30 6.02.31.png$

Solución

Declaraciones	Razones
1. $QR = TR$	1. Dado.
2. $\angle Q = \angle T.$	2. Los ángulos interiores alternos de líneas paralelas ($QP \|\| ST$) son iguales.
3. $\angle PRQ = \angle SRT$.	3. Los ángulos verticales son iguales.
4. $\triangle PQR \cong \triangle STR$.	4. $ASA = ASA: \angle Q, QR, \angle R$de$\triangle PQR = \angle T$,$TR, \angle R$ de$\triangle STR$.
5. $PR = SR$.	5. Los lados correspondientes de los triángulos congruentes son iguales,

Problemas

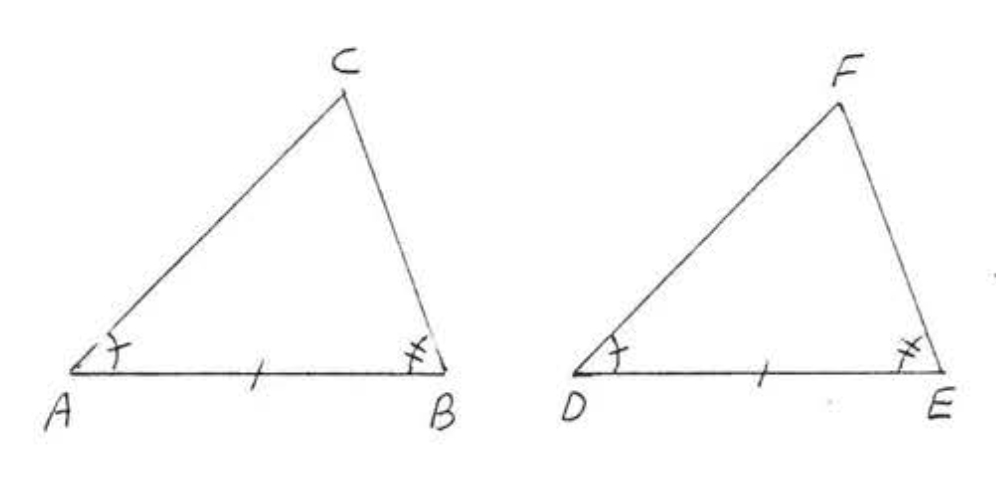
1. Dado$\angle A = \angle D$,$\angle B = \angle E$,$AB = DE$. Demostrar$AC = DF$.

$Screen Shot 2020-10-30 a las 6.14.23 PM.png$

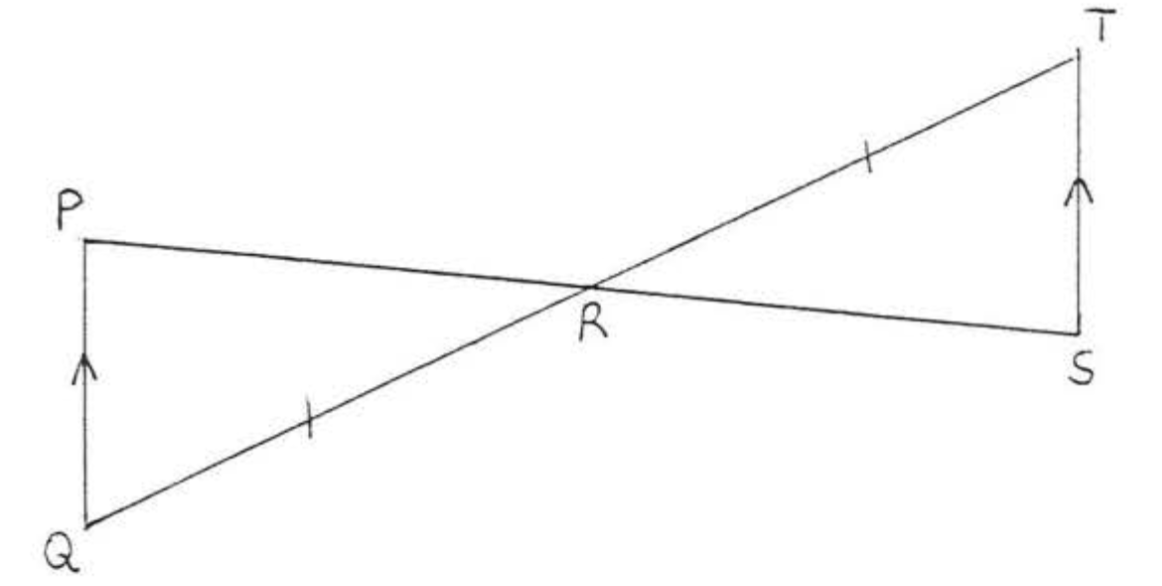
2. Dado$AC= DF$,$BC = EF$,$\angle C = \angle F$. Demostrar$AB = DE$.

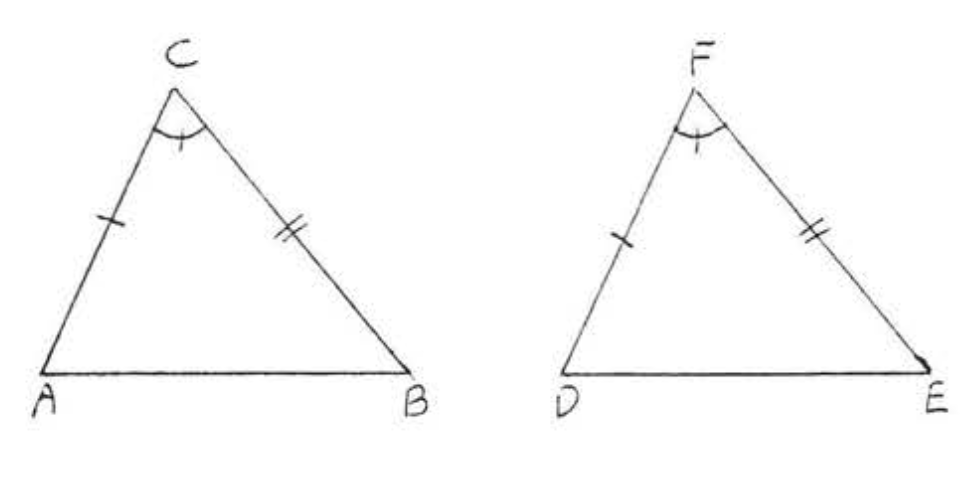
$Screen Shot 2020-10-30 a las 6.14.42 PM.png$

3. Dado$AC = EC$ y$BC = DC$. Demostrar$AB = ED$.

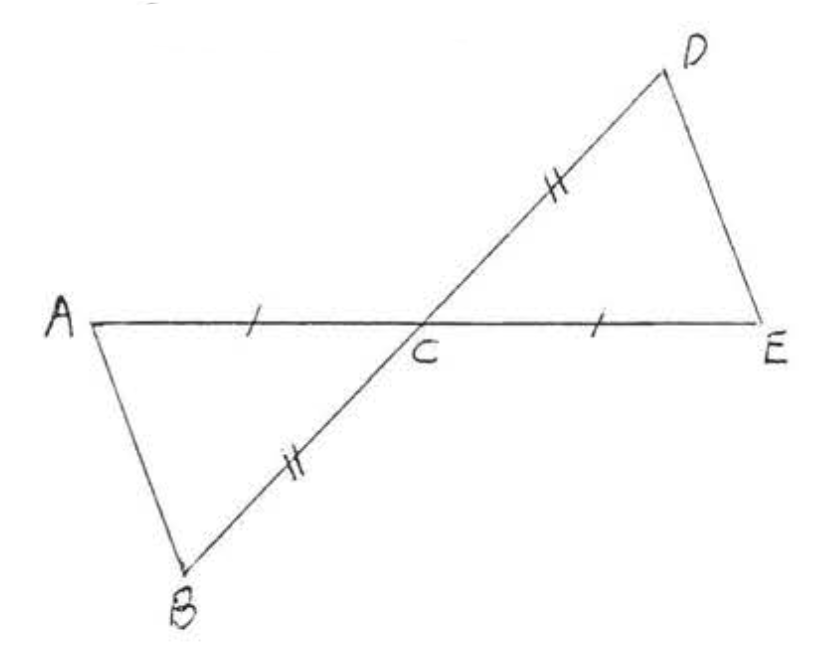
$Screen Shot 2020-10-30 a las 6.15.21 PM.png$

4. Dado$AC = DC$,$\angle A = \angle D$. Demostrar$BC = EC$.

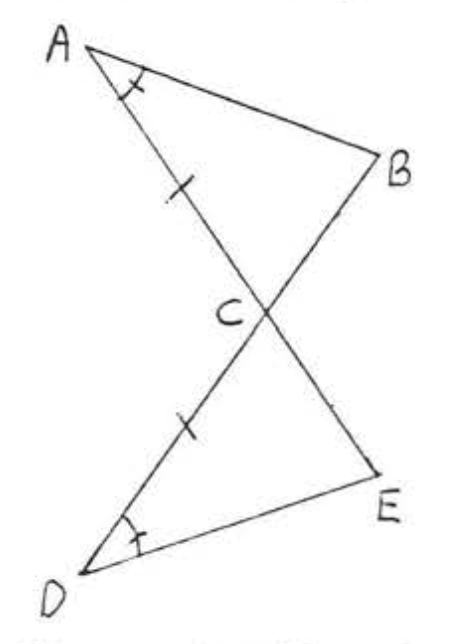
$Screen Shot 2020-10-30 a las 6.15.36 PM.png$

5. Dado$\angle ABD = \angle CDB$ y$\angle ADB = \angle CBD$. Demostrar$AB = CD$.

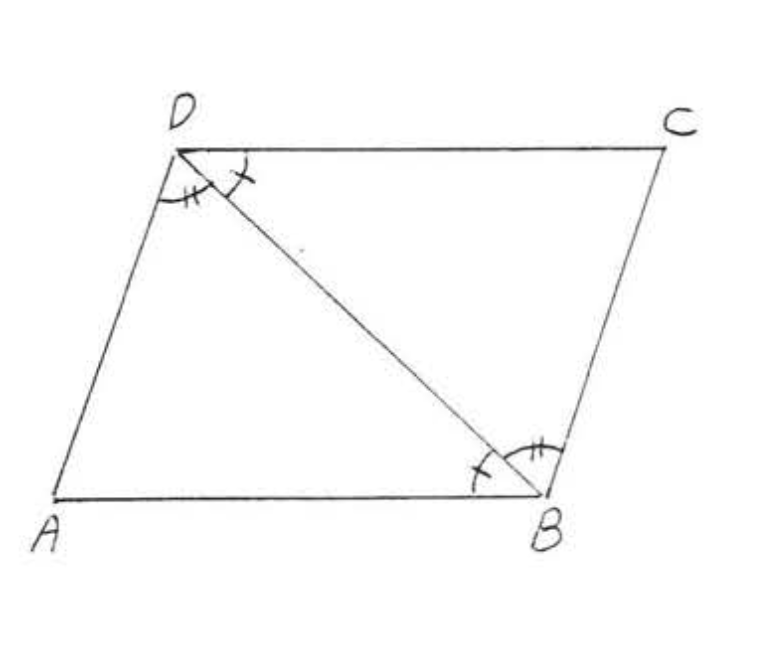
$Screen Shot 2020-10-30 a las 6.15.48 PM.png$

6. Dado$AB || CD$ y$AD || CB$. Demostrar$AB = CD$.

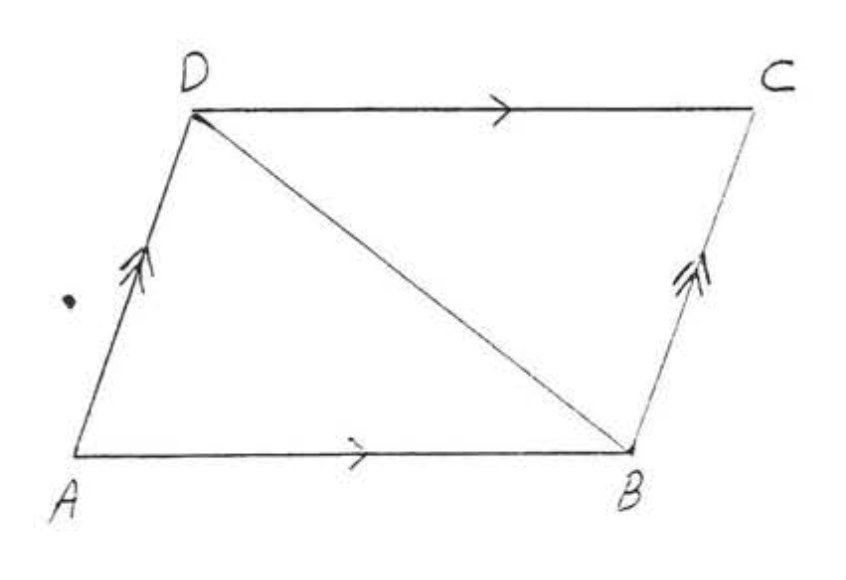
$Screen Shot 2020-10-30 a las 6.15.59 PM.png$

7. Dado$AC = BC$ y$\angle ACD = \angle BCD$. Demostrar$\angle A = \angle B$.

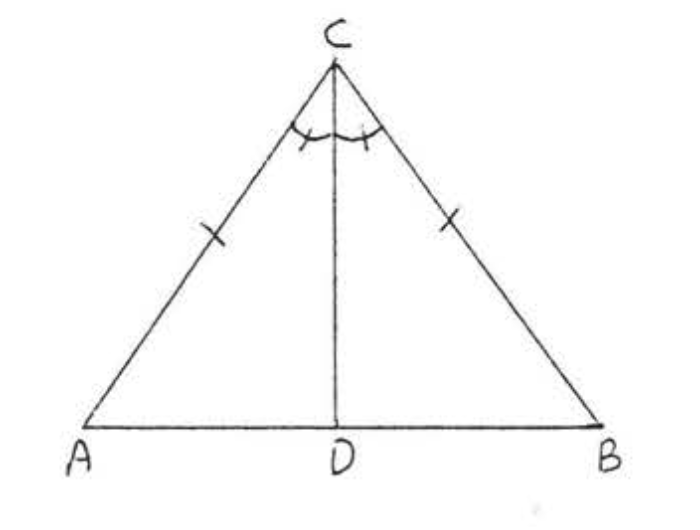
$Screen Shot 2020-10-30 a las 6.16.32 PM.png$

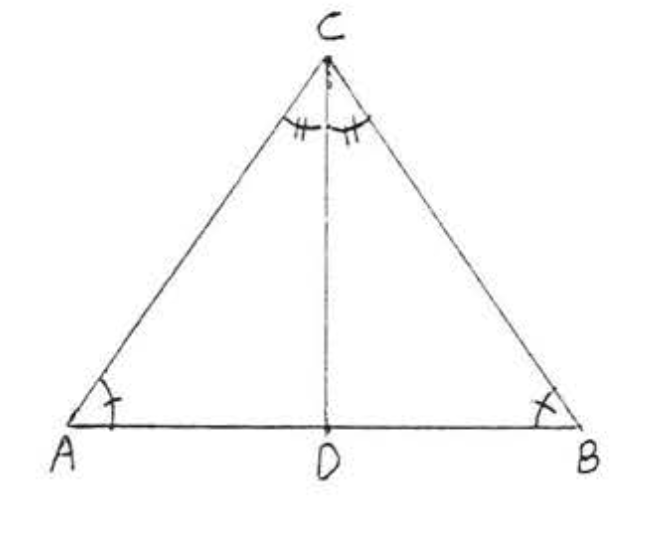
8. Dado$\angle A = \angle B$,$\angle ACD = \angle BCD$. Demostrar$AC = BC$.

$Screen Shot 2020-10-30 a las 6.16.45 PM.png$

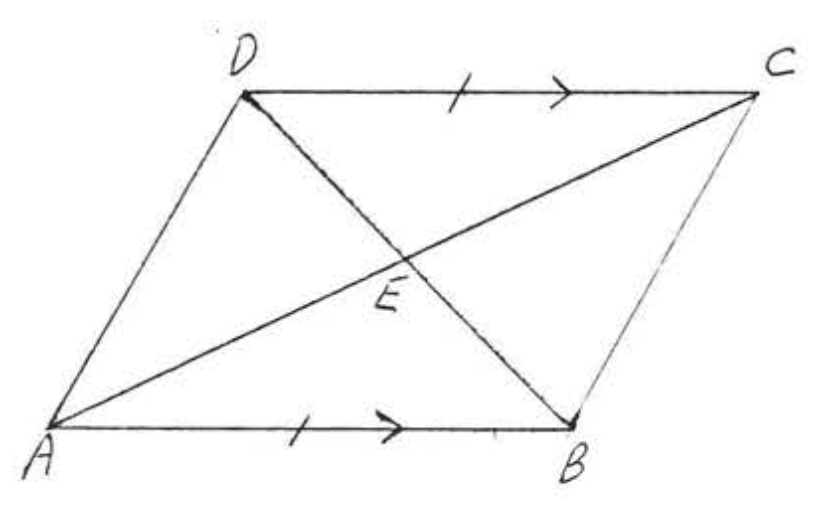
9. Dado$AB || CD$ y$AB = CD$. Demostrar$AE = CE$. (Pista: Mostrar$\triangle ABE \cong \triangle CDE$)

$Screen Shot 2020-10-30 a las 6.16.58 PM.png$

10. Dado$AE = CE$ y$BE = DE$. Demostrar$\angle BAC = \angle CDB$.

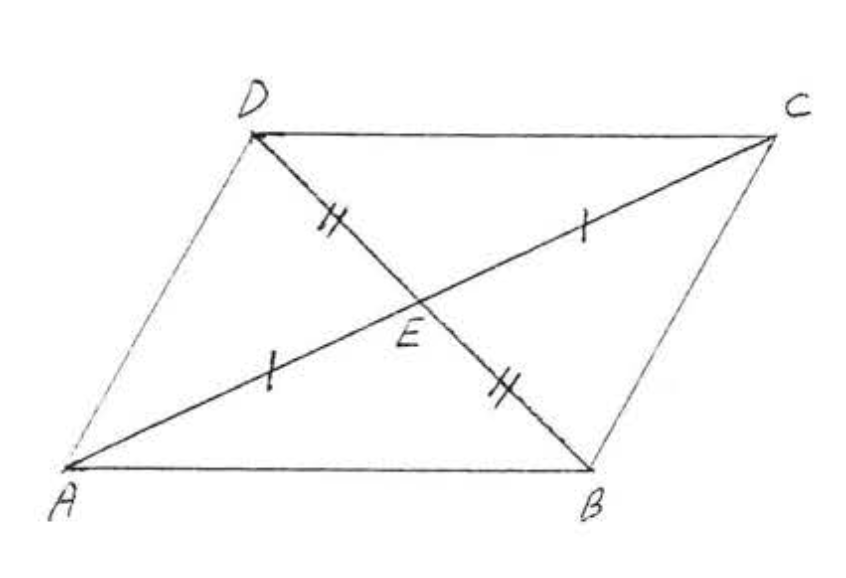
$Screen Shot 2020-10-30 a las 6.17.17 PM.png$

11. Dado$\angle A = \angle D$,$AC = DE$,$AB || DC$. Demostrar$BC = CE$.

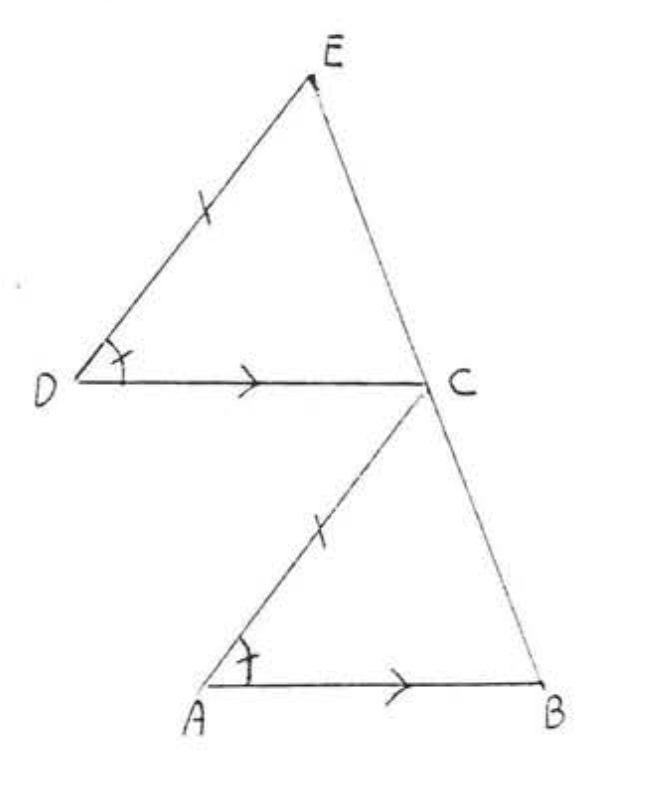
$Screen Shot 2020-10-30 a las 6.17.30 PM.png$

12. Dado$AB || DE$,$AC || FE$ y$DC = FE$. Demostrar$BE = EC$.

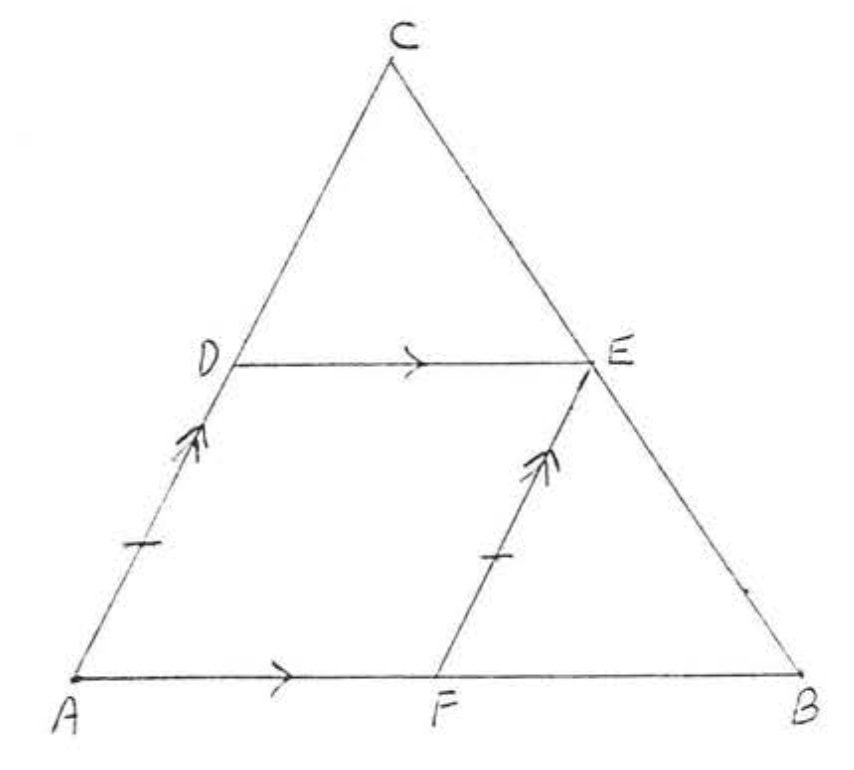
$Screen Shot 2020-10-30 a las 6.17.55 PM.png$

13. Dado$AD = BC$ y$\angle BAD = \angle ABC$. Demostrar$AC = BD$. (Pista: Mostrar$\triangle ABD \cong \triangle BAC$)

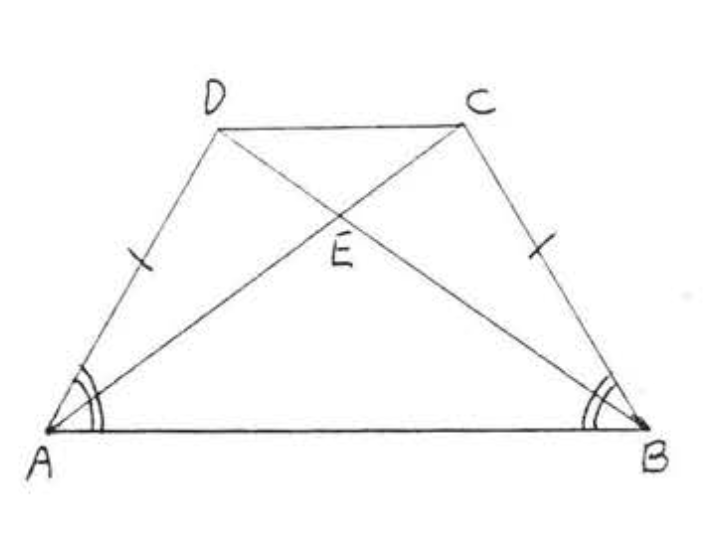
$Screen Shot 2020-10-30 a las 6.18.11 PM.png$

14. Dado$AD = BE$,$\angle BAC = \angle ABC$. Demostrar$AE = BD$.

$Screen Shot 2020-10-30 a las 6.18.26 PM.png$

Declaraciones	Razones
1. \(AB = CD\).	1. Dado.
2. \(\angle ABD = \angle CDB\).	2. Los ángulos interiores alternos de las líneas paralelas\((AB \|\| CD)\) son iguales.
3. \(BD = DB\).	3. Identidad.
4. \(\triangle ABD \cong \triangle CDB\)	4. \(SAS = SAS\):\(AB, \angle B, BD\) de\(\triangle ABD = CD\),\(\angle D\),\(DB\) de\(\triangle CDB\).
5. \(AD = BC\)	5. Los lados correspondientes de los triángulos congruentes son iguales,

Declaraciones	Razones
1. \(QR = TR\)	1. Dado.
2. \(\angle Q = \angle T.\)	2. Los ángulos interiores alternos de líneas paralelas (\(QP \|\| ST\)) son iguales.
3. \(\angle PRQ = \angle SRT\).	3. Los ángulos verticales son iguales.
4. \(\triangle PQR \cong \triangle STR\).	4. \(ASA = ASA: \angle Q, QR, \angle R\)de\(\triangle PQR = \angle T\),\(TR, \angle R\) de\(\triangle STR\).
5. \(PR = SR\).	5. Los lados correspondientes de los triángulos congruentes son iguales,

Ejemplo\(\PageIndex{1}\)

Ejemplo\(\PageIndex{2}\)

Problemas