2.6: El Teorema del SSS
- Page ID
- 114602
Consideramos ahora el caso donde se sabe que el lado de dos triángulos es de la misma longitud.
Dos triángulos son congruentes si tres lados de uno son iguales respectivamente a tres lados del otro (\(SSS = SSS\)).
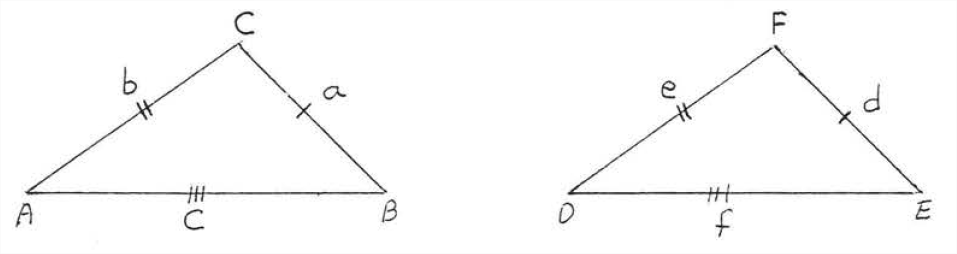
Teorema\(\PageIndex{1}\) se demuestra en la Figura\(\PageIndex{1}\): si\(a=d, b=e,\) y\(c=f\) luego\(\triangle ABC \cong \triangle DEF\)
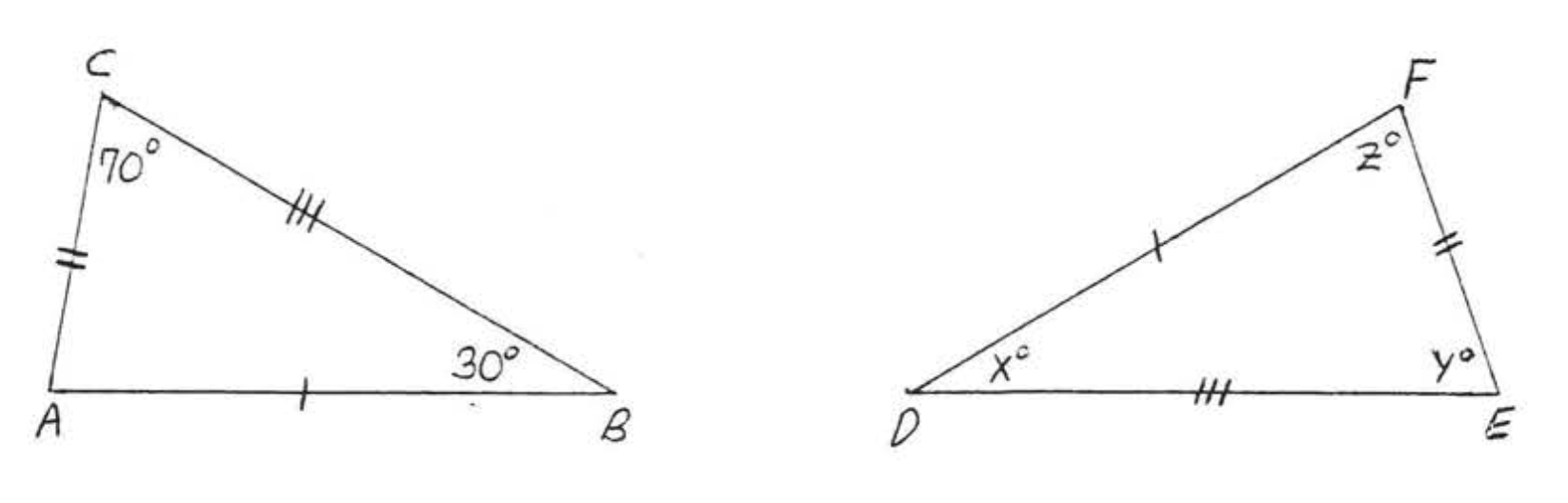
Encuentra\(x, y, z:\)
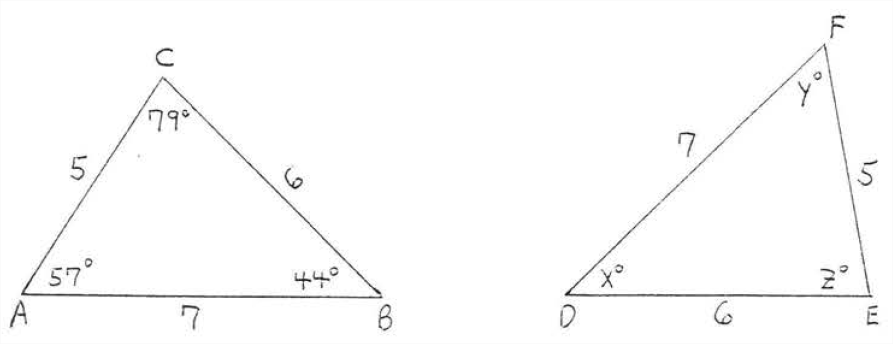
Solución
\(AB = 7 = DF\). Por lo tanto\(\angle C,\) el ángulo opuesto AB debe corresponder\(\angle E\), el ángulo opuesto\(DF\). De la misma manera\(\angle A\) corresponde\(\angle F\) y\(\angle B\) corresponde a\(\angle D\). Tenemos\(\triangle ABC \cong \triangle FDE\) por\(SSS = SSS\), entonces
\(x^{\circ}=\angle D=\angle B=44^{\circ}\)
\(y^{\circ}=\angle F=\angle A=57^{\circ}\)
\(z^{\circ}=\angle E=\angle C=79^{\circ}\)
Respuesta:\(x = 44, y=57, z=79\)
En Figura\(\PageIndex{1}\), lugar\(\triangle ABC\) y\(\triangle DEF\) para que sus lados más largos coincidan, en este caso\(AB\) y\(DE\). Esto se puede hacer porque\(AB = c= r = DE.\) Ahora dibuja\(CF\), formando ángulos\(1,2,3,\) y 4 (Figura\(\PageIndex{2}\)). El resto de la prueba se presentará en forma de doble columna:
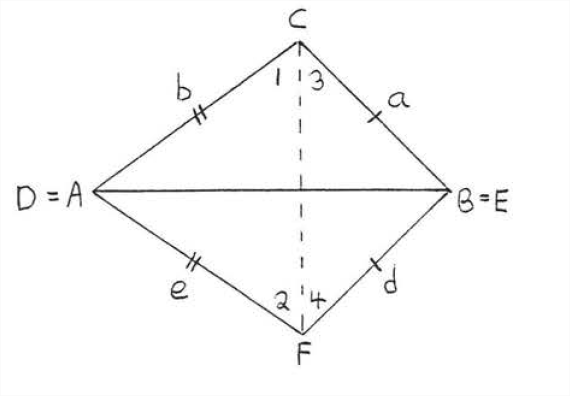
| Comunicado | Razones |
| 1. \(\angle 1 = \angle 2\). | 1. Los ángulos base del triángulo isósceles\(CAF\) son iguales (Teorema\(\PageIndex{1}\), section 2.5). |
| 2. \(\angle 3 = \angle 4\). | 2. Los ángulos base del triángulo isósceles\(CBF\) son iguales. |
| 3. \(\angle C = \angle F\). | 3. \(\angle C = \angle 1 + \angle 3 = \angle 2 + \angle 4 = \angle F\). |
| 4. \(AC = DF\). | 4. Dado,\(AC = b = e = DF\). |
| 5. \(BC = EF\). | 5. Dado,\(BC = a = d = EF\). |
| 6. \(\triangle ABC \cong \triangle DEF\). | 6. \(SAS = SAS\):\(AC, \angle C, BC\) de\(\triangle ABC = DF\),\(\angle F\),\(EF\) de\(\triangle DEF\). |
Dado\(AB = DE, BC = EF,\) y\(AC = DF\). Demostrar\(\angle C = \angle F\)
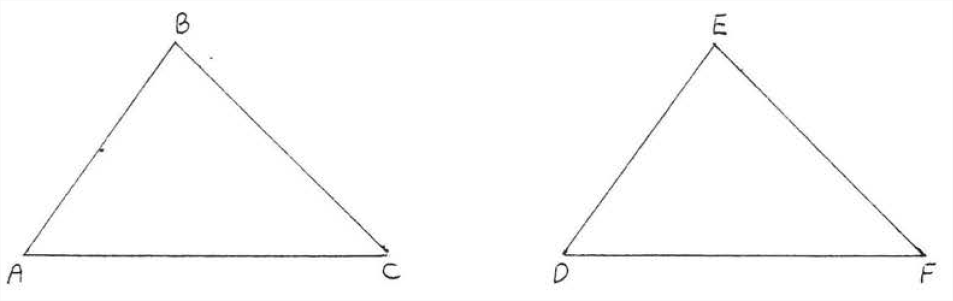
Solución
| Declaraciones | Razones |
| 1. \(AB = DE\). | 1. Dado. |
| 2. \(BC = EF\). | 2. Dado. |
| 3. \(AC = DF\). | 3. Dado. |
| 4. \(\triangle ABC \cong \triangle DEF\). | 4. \(SSS = SSS\):\(AB, BC, AC\) de\(\triangle ABC = DE\),\(EF, DF\) de\(\triangle DEF\). |
| 5. \(\angle C = \angle F\). | 5. Los ángulos correspondientes de los triángulos congruentes son iguales. |
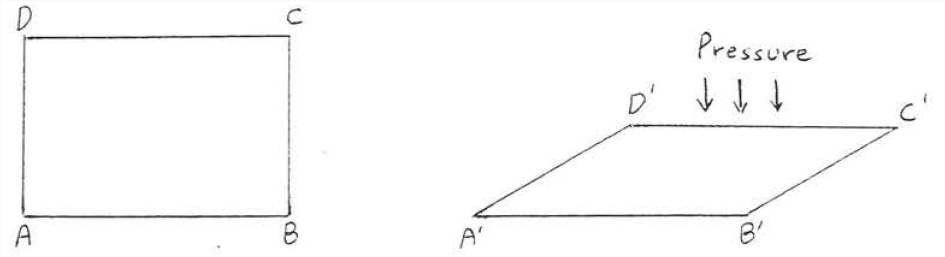
El Teorema de SSS es la base de un importante principio de ingeniería de construcción llamado refuerzo triangular. Imagine que los segmentos de línea en la Figura\(\PageIndex{3}\) son granos de madera o acero unidos en los extremos por clavos o tornillos. Si se aplica presión a uno de los lados,\(ABCD\) se colapsará y se verá como\(A'B'C'D'\).
Ahora supongamos puntos\(A\) y\(C\) están unidos por una nueva viga, llamada corsé (Figura\(\PageIndex{4}\)). La estructura no colapsará mientras los frijoles permanezcan intactas y unidos entre sí. Es imposible deformarse\(ABCD\) en cualquier otra forma\(A'B'C'D'\) porque si\(AB = A'B'\),\(BC = B'C'\), y\(AC = A'C'\) entonces\(\triangle ABC\) sería congruente a\(\triangle A'B'C'\) por\(SSS = SSS\).
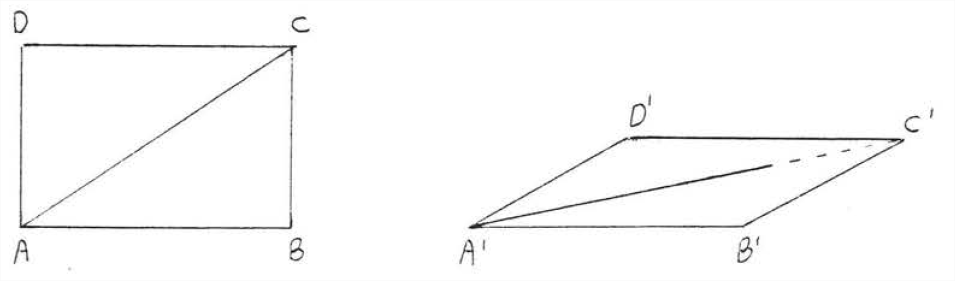
A veces decimos que un triángulo es una figura rígida; una vez fijados los lados de un triángulo no se pueden cambiar los ángulos. Así, en la Figura\(\PageIndex{4}\), la forma de\(\triangle ABC\) no se puede cambiar siempre y cuando las longitudes de sus lados permanezcan iguales.
Problemas
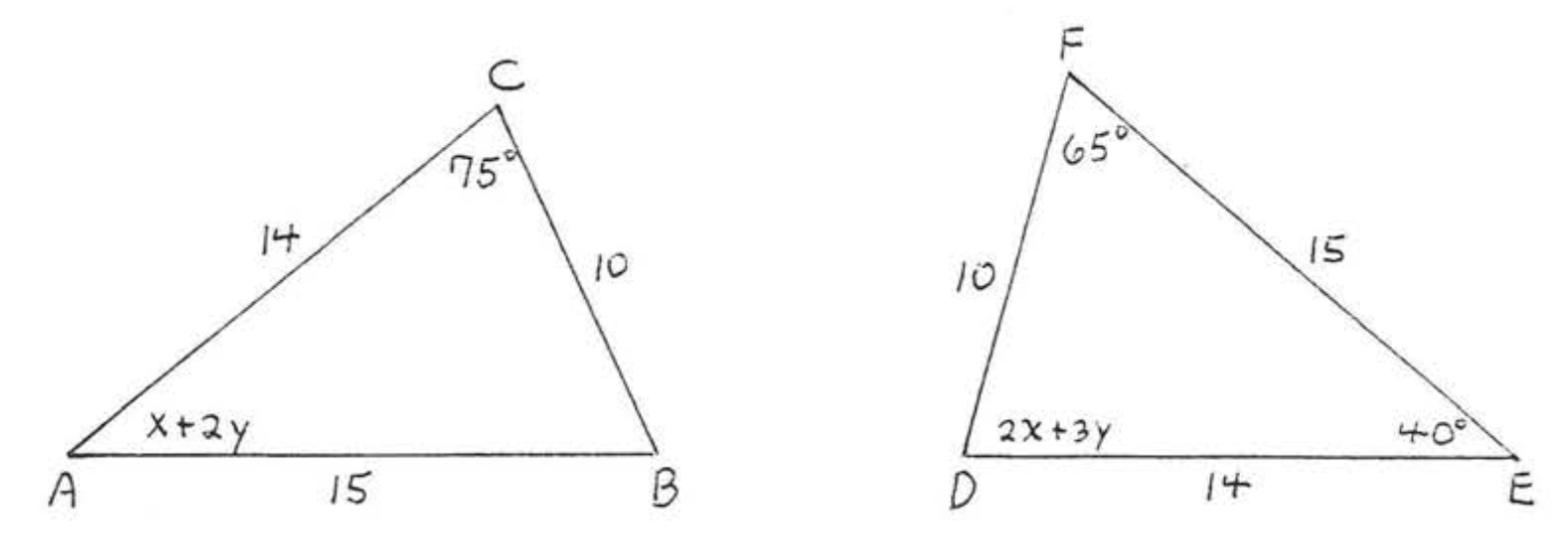
1 - 8. Para cada uno de los siguientes (1) escribir la declaración de congruencia,
(2) dada la razón de (1) (\(SAS\),\(ASA\)\(AAS\), o\(SSS\) teorema), y
(3) encontrar\(x\), o\(x\) y\(y\), o\(x, y\), y\(z\).
1.
2.
3.
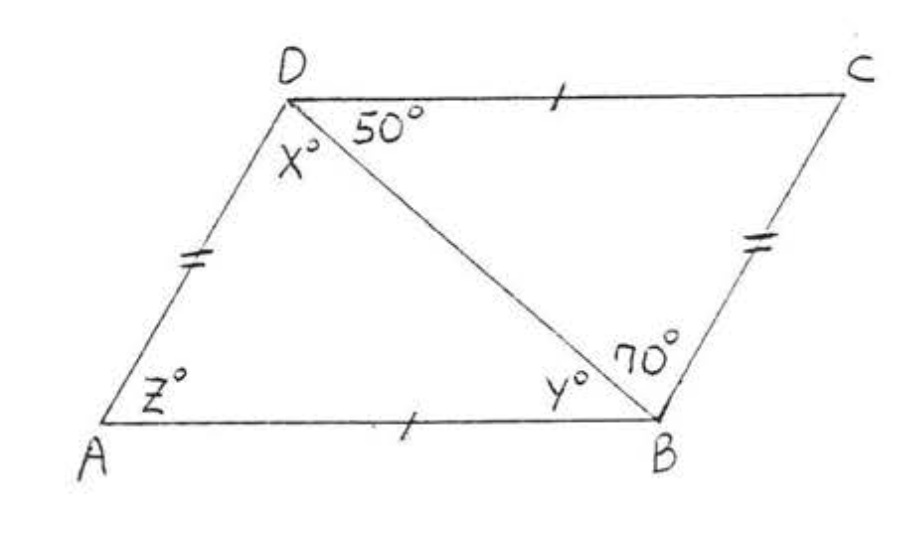
4.
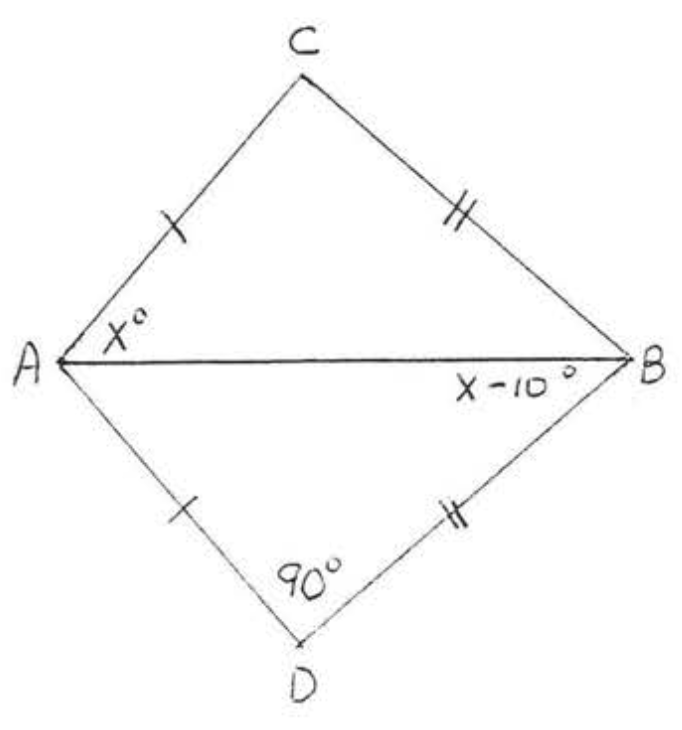
5.
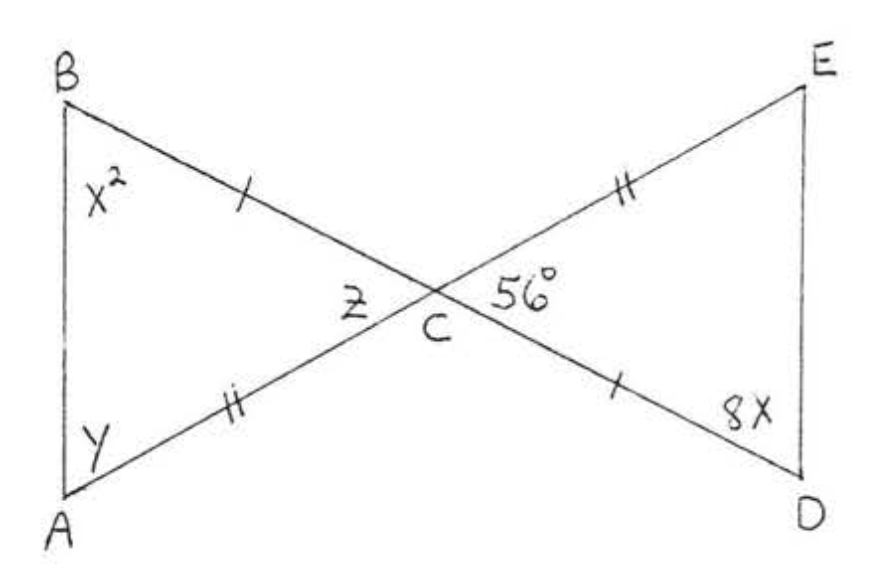
6.
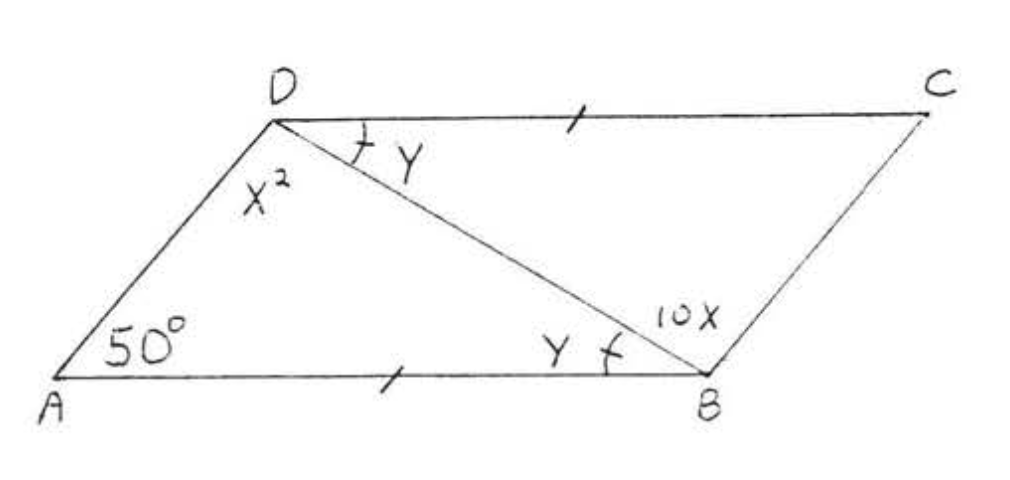
7.
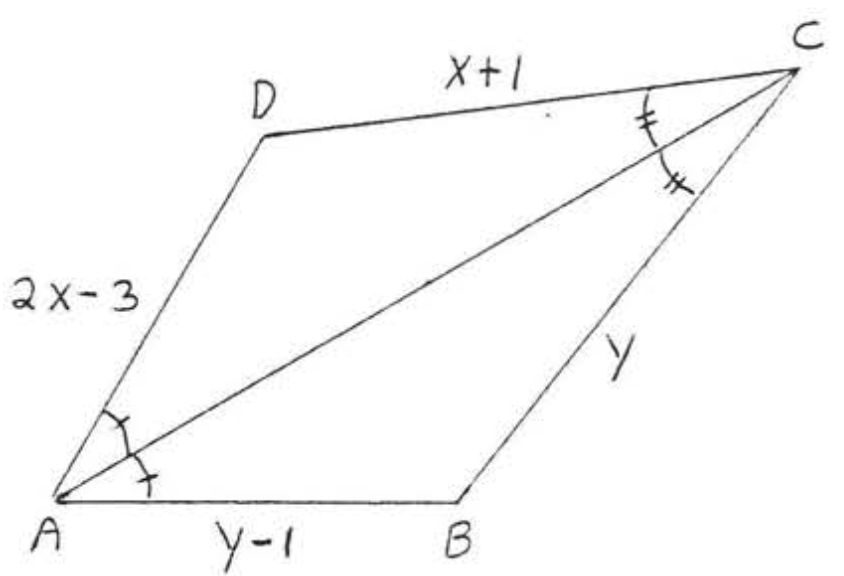
8.
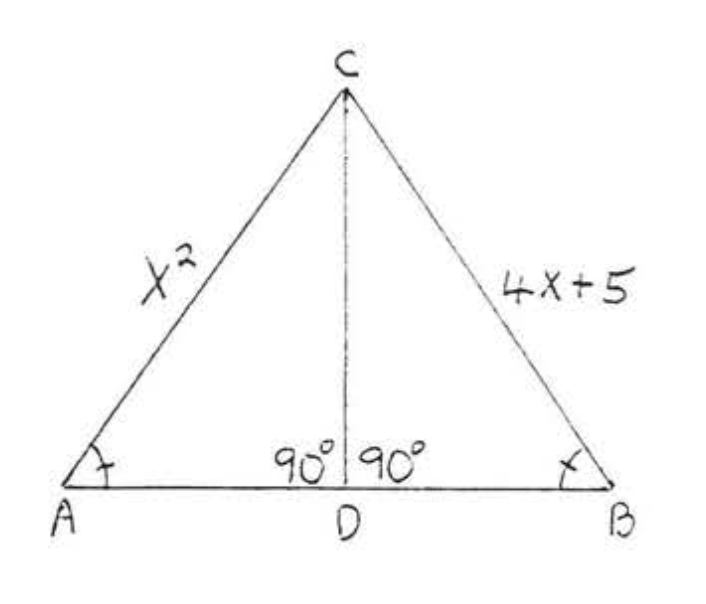
9. Dado\(AB = DE\),\(BC = EF\), y\(AC = DF\). Demostrar\(\angle A = \angle D\).
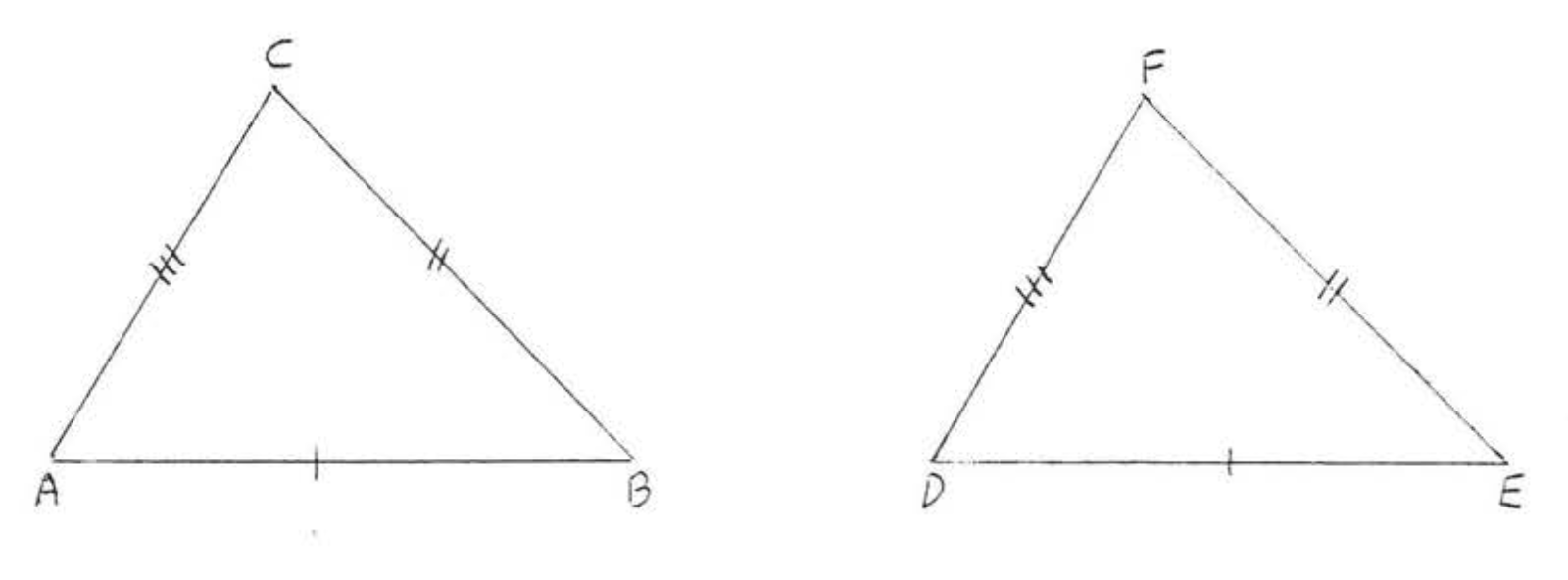
10. Dado\(AC = BC\). \(AD = BD\). Demostrar\(\angle ADC = \angle BDC\).
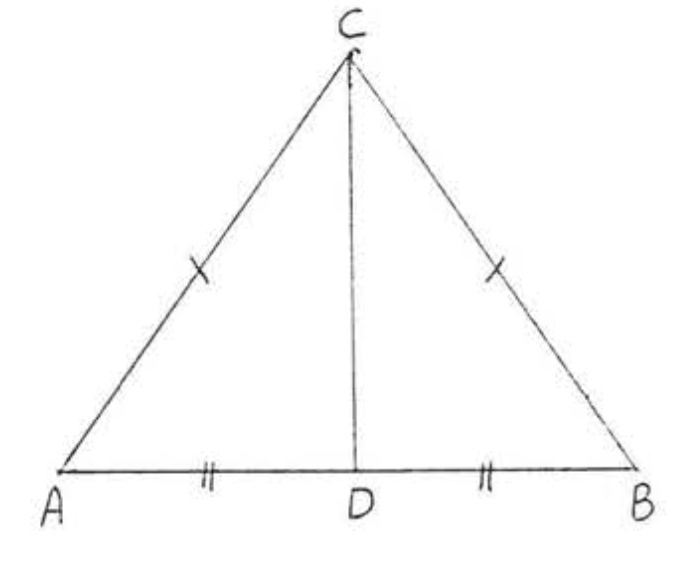
11. Dado\(AB = AD\),\(BC = DC\). Demostrar\(\angle BAC = \angle CAD\).
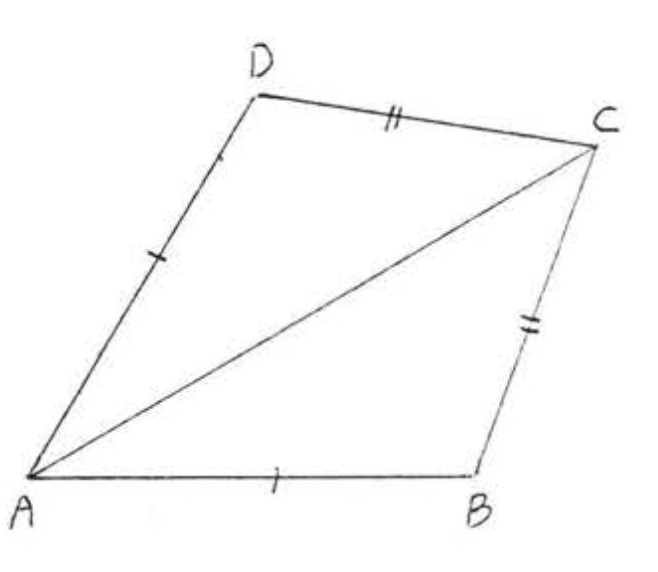
12. Dado\(AB = CD\),\(BC = DA\). Demostrar\(\angle BAC = \angle DCA\).
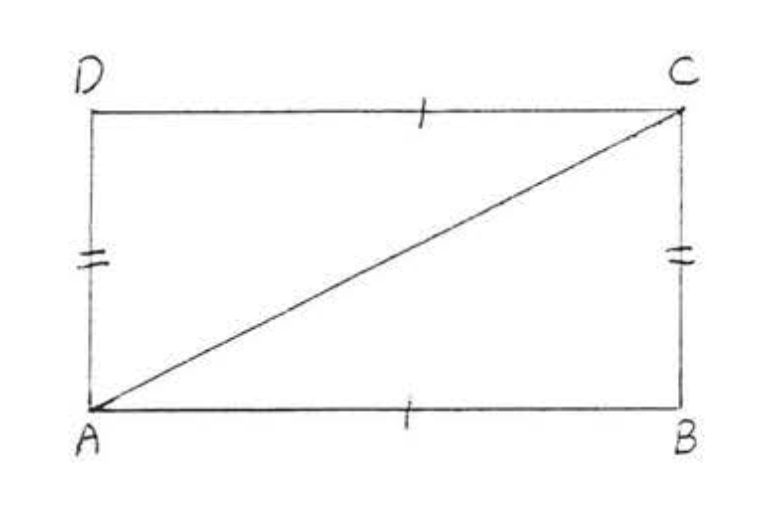
13. Dado\(AE = CE\),\(BE = ED\). Demostrar\(AB = CD\).
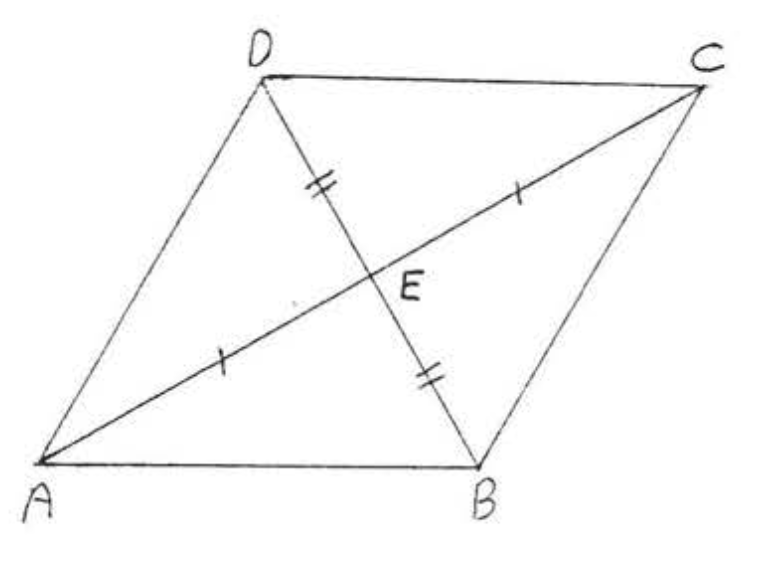
14. Dado\(AB||CD\),\(AD||BC\). Demostrar\(AB = CD\).