5.2: Solución de Triángulos Rectos
- Page ID
- 114552
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)En la sección anterior mostramos que todos los\(30^{\circ}\) ángulos tienen los mismos valores trigonométricos. Si calculamos cada uno de estos valores a cuatro decimales, obtenemos\(\sin 30^{\circ} = \dfrac{1}{2} = 0.5000\),\(\cos 30^{\circ} = \dfrac{\sqrt{3}}{2} = \dfrac{1.73205}{2} = 0.8660\), y\(\tan 30^{\circ} = \dfrac{\sqrt{3}}{3} = \dfrac{1.73205}{3} = 0.5774\). Estos números aparecen en la tabla de valores trigonométricos de la página 356 en la fila correspondiente a\(30^{\circ}\).
Como puedes ver, esta tabla contiene los valores trigonométricos de ángulos de\(1^{\circ}\) a\(90^{\circ}.\) No es práctico computar la mayoría de estos valores directamente, por lo que usaremos esta tabla cuando los necesitemos. También se puede utilizar una calculadora de bolsillo con funciones trigonométricas.
Encontrar\(\sin 20^{\circ}\),\(\cos 20^{\circ},\), y\(\tan 20^{\circ}\).
Solución
Busque\(20^{\circ}\) en la columna de ángulo de la tabla de la página 356:
Si estás usando una calculadora de bolsillo, primero asegúrate de que esté en modo grados. Luego escribe 20, seguido de las claves pecado, cos, o bronceado.
Respuesta:\(\sin 20^{\circ}=0.3420\),\(\cos 20^{\circ}=0.9397\),\(\tan 20^{\circ}=0.3640\)
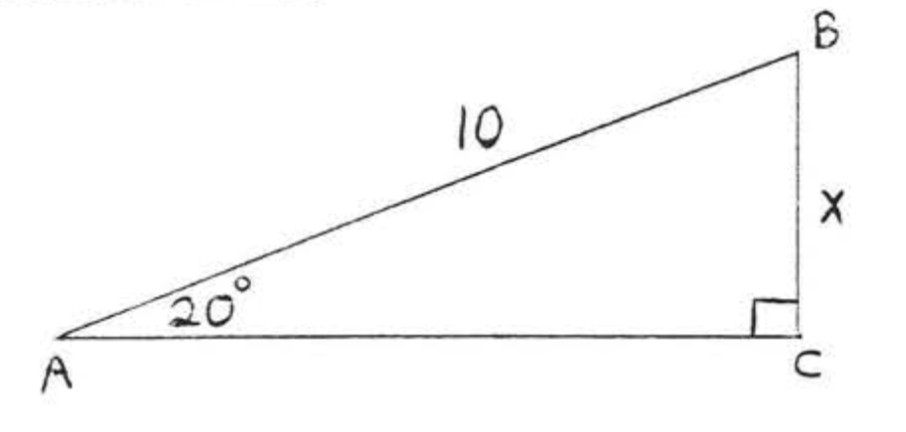
Encuentra\(x\) a la décima más cercana:
Solución
Deseamos encontrar la pierna opuesta\(20^{\circ}\) y conocemos la hipotenusa. Usamos el seno porque es la única de las tres funciones trigonométricas que involucra tanto la pierna opuesta como la hipotenusa.
\(\begin{array} {rcl} {\sin 20^{\circ}} & = & {\dfrac{\text{opp}}{\text{hyp}}} \\ {.3420} & = & {\dfrac{x}{10}} \\ {(10)(.3420)} & = & {\dfrac{x}{\cancel{10}} \cancel{(10)}} \\ {3.420} & = & {x} \end{array}\)
Si está utilizando una calculadora de bolsillo, escriba
Respuesta:\(x = 3.4\)
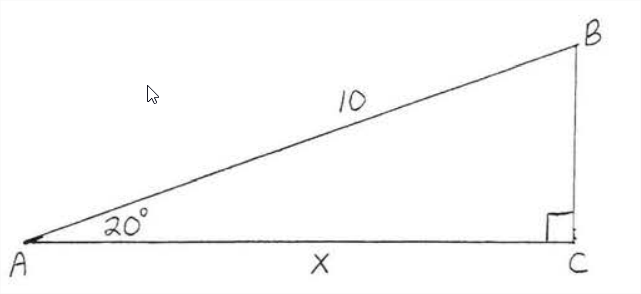
Encuentra\(x\) a la décima más cercana:
Solución
Conocemos la hipotenusa y deseamos encontrar la pierna adyacente a\(\angle A\). Por lo tanto, utilizamos el coseno.
\(\begin{array} {rcl} {\cos 20^{\circ}} & = & {\dfrac{\text{adj}}{\text{hyp}}} \\ {0.9397} & = & {\dfrac{x}{10}} \\ {9.397} & = & {x} \end{array}\)
Si está utilizando una calculadora de bolsillo, escriba
Respuesta:\(x = 9.4\)
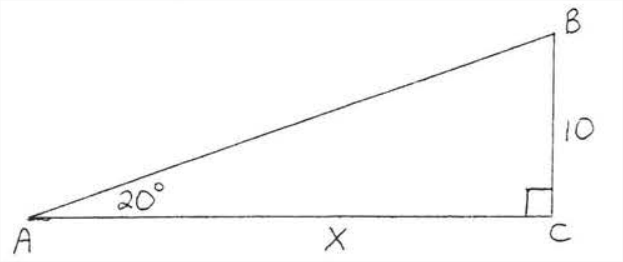
Encuentra\(x\) a la décima más cercana:
Solución
Conocemos la pierna opuesta\(\angle A\) y deseamos encontrar la pierna adyacente a\(\angle A\). Por lo tanto, utilizamos la tangente.
\(\begin{array} {rcl} {\tan 20^{\circ}} & = & {\dfrac{\text{opp}}{\text{adj}}} \\ {.3640} & = & {\dfrac{10}{x}} \\ {(x)(0.3640)} & = & {(\dfrac{10}{\cancel{x}})\cancel{(x)}} \\ {0.3640x} & = & {10} \\ {\dfrac{0.3640 x}{0.3640}} & = & {\dfrac{10}{0.3640}} \\ {x} & = & {\dfrac{10}{0.3640} = \dfrac{10}{0.364} = 27.47} \end{array}\)
27.47 se obtiene por división larga:
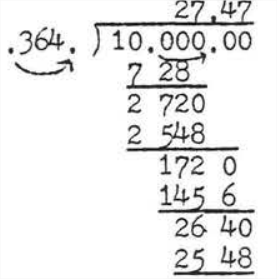
Si está utilizando una calculadora de bolsillo, escriba
Respuesta:\(x = 27.5\)
Hay un método más fácil de resolver Ejemplo\(\PageIndex{4}\). \(\angle B = 90^{\circ}-20^{\circ} = 70^{\circ}\)La pierna opuesta\(\angle B\) es\(x\) y la pata adyacente a\(\angle B\) es 10.
\(\begin{array} {rcl} {\tan 70^{\circ}} & = & {\dfrac{\text{opp}}{\text{adj}}} \\ {2.7475} & = & {\dfrac{x}{10}} \\ {(2.7475)(10)} & = & {x} \\ {27.475} & = & {x} \\ {27.5} & = & {x} \end{array}\)
Este método es más fácil porque implica multiplicación en lugar de división larga.
Encuentra\(x\) a la décima más cercana:
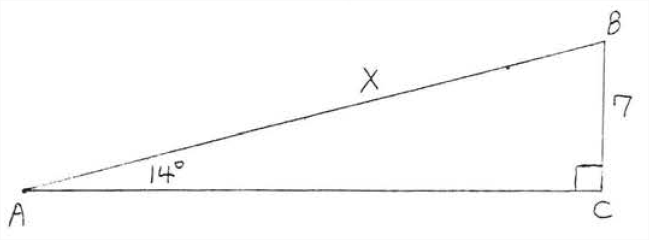
Solución
\(\begin{array} {rcl} {\sin 14^{\circ}} & = & {\dfrac{\text{opp}}{\text{hyp}}} \\ {.2419} & = & {\dfrac{7}{x}} \\ {.2419 x} & = & {7} \\ {x} & = & {\dfrac{7}{.2419} = 28.9} \end{array}\)
En este caso no hay manera de evitar la división larga. (Es posible evitar la división larga introduciendo tablas para las funciones secante y cosecante. No lo haremos en este libro.)
Respuesta:\(x = 28.9\)
Encuentra\(x\) al grado más cercano:
Solución
\(\begin{array} {rcl} {\sin 14^{\circ}} & = & {\dfrac{\text{opp}}{\text{hyp}}} \\ {.2419} & = & {\dfrac{7}{x}} \\ {.2419 x} & = & {7} \\ {x} & = & {\dfrac{7}{.2419} = 28.9} \end{array}\)
En este caso no hay manera de evitar la división larga. (Es posible evitar la división larga introduciendo tablas para las funciones secante y cosecante. No lo haremos en este libro.)
Respuesta:\(x = 28.9\)
Encuentra\(x\) al grado más cercano:
Solución
\(\begin{array} {rcl} {\sin x^{\circ}} & = & {\dfrac{\text{opp}}{\text{hyp}}} \\ {\sin x^{\circ}} & = & {\dfrac{2}{3} = .6667} \end{array}\)
En la tabla buscamos en la columna seno el valor más cercano a .6667:
| Ángulo | Sine |
| . | . |
| . | . |
| \(41^{\circ}\) | .6561 |
| \(42^{\circ}\) | .6691 |
| . | . |
.6667 es el más cercano a .6691 porque .6691 - .6667 = .0024 mientras que .6667 - .6561 = .0106. Por lo tanto\(x^{\circ} = 42^{\circ}\), al grado más cercano.
Si estás usando una calculadora de bolsillo, necesitarás usar el INV sin o 2nd F sin o el MAYÚS sin o\(sin^{-1}\) las teclas, dependiendo del modelo de calculatore. Tipo 2\(\div\) 3 = INV sin, luego redondea al grado más cercano.
Respuesta:\(x = 42\)
Encuentra\(x\) a la décima más cercana:
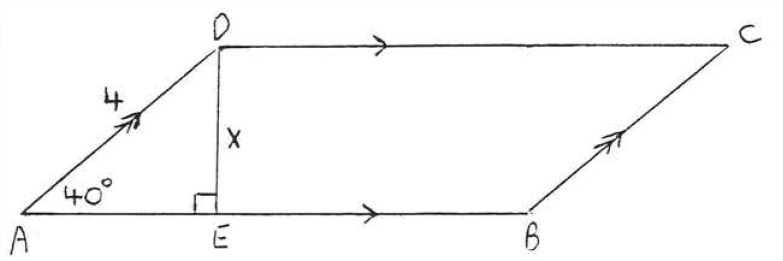
Solución
\(\begin{array} {rcl} {\sin 40^{\circ}} & = & {\dfrac{\text{opp}}{\text{hyp}}} \\ {.6428} & = & {\dfrac{x}{4}} \\ {(4)(.6428)} & = & {\dfrac{x}{\cancel{4}} (\cancel{4})} \\ {2.5712} & = & {x} \\ {2.6} & = & {x} \end{array}\)
Respuesta:\(x = 2.6\).
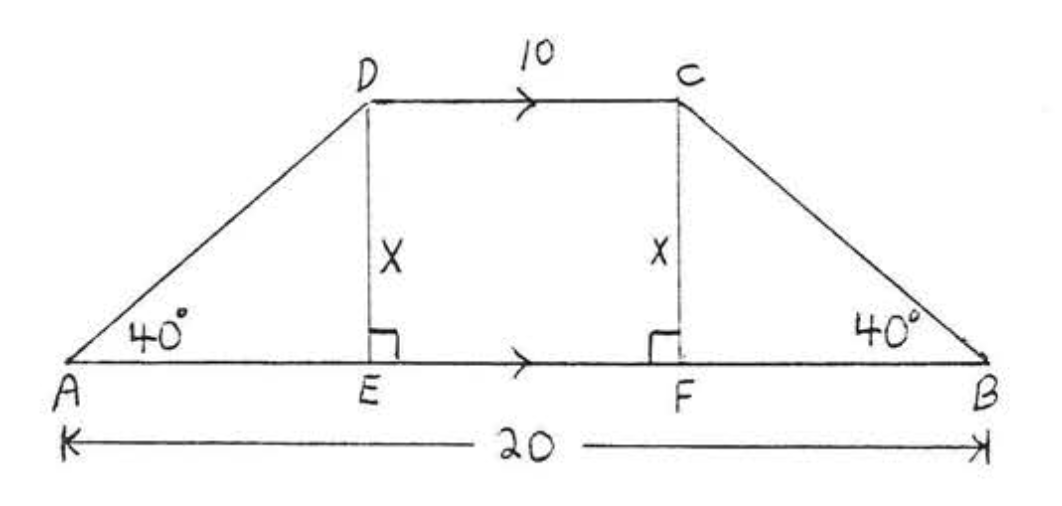
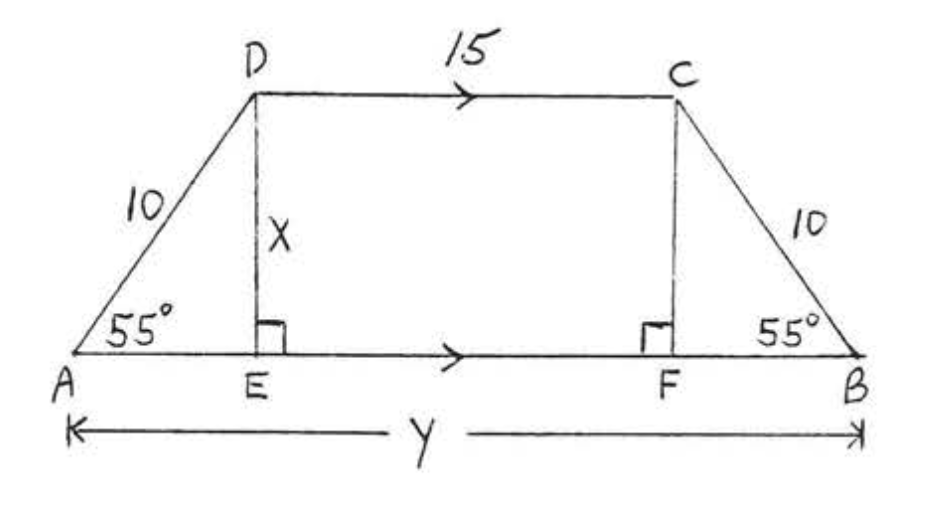
Encuentra\(x\) y\(y\) al décimo más cercano:
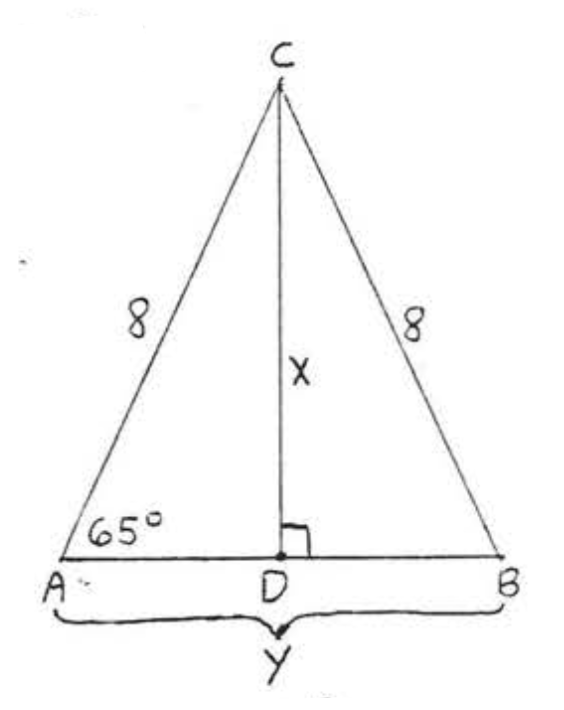
Solución
\(\begin{array} {rcl} {\sin 65^{\circ}} & = & {\dfrac{\text{opp}}{\text{hyp}}} \\ {.9063} & = & {\dfrac{x}{8}} \\ {(8)(.9063)} & = & {\dfrac{x}{\cancel{8}} (\cancel{8})} \\ {7.2504} & = & {x} \\ {7.3} & = & {x} \end{array}\)
Para encontrar primero\(y\) encontramos\(AD\):
\(\begin{array} {rcl} {\cos 65^{\circ}} & = & {\dfrac{\text{adj}}{\text{hyp}}} \\ {.4226} & = & {\dfrac{AD}{8}} \\ {(8)(.4226)} & = & {\dfrac{AD}{8} (8)} \\ {3.3808} & = & {AD} \end{array}\)
Ya\(AC = BC = 8\) que tenemos\(\angle A = \angle B = 65^{\circ}\). Por lo tanto\(BD = AD = 3.3808\). \(y = AD + BD = 3.3808 + 3.3808 = 6.7616 = 6.8\).
Respuesta:\(x = 7.3, y = 6.8\).
La primera tabla de valores trigonométricos fue construida por el astrónomo griego Hiparco (c. 180-125 a.C.). Hiparco asumió que el vértice de cada ángulo era el centro de un círculo, como\(\angle AOB\) se muestra en el círculo de la Figura\(\PageIndex{1}\). Dependiendo del número de grados en\(\angle AOB\), su tabla daría la longitud del acorde\(AB\) relativo al radio del círculo. Hoy mediríamos\(\angle AOC\) en lugar de\(\angle AOB\) y usaríamos el medio acorde\(AC\) en lugar de\(AB\). La relación\(\dfrac{AC}{AO}\) es entonces solo el seno de\(\angle AOC\).
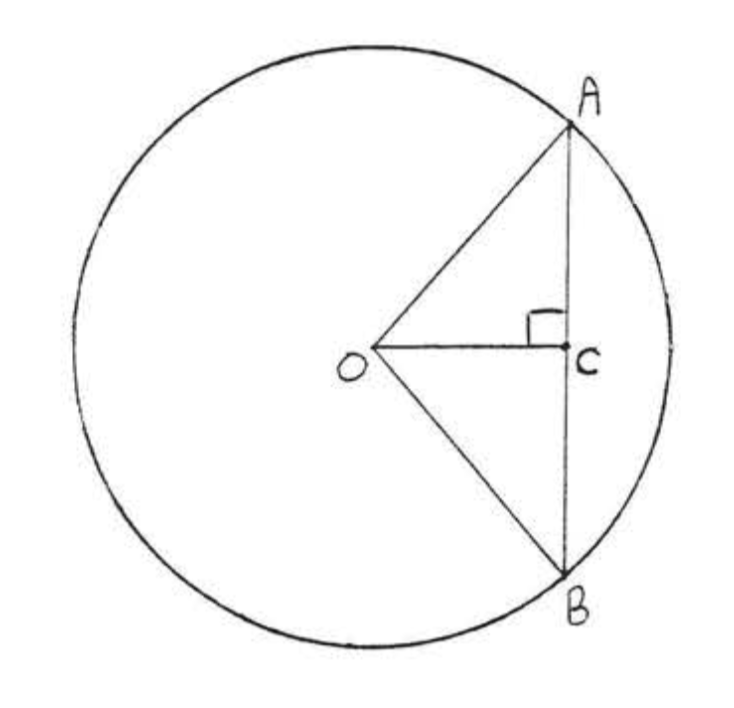
Hiparco obtuvo algunos de los valores para su tabla a partir de las propiedades de figuras geométricas especiales, como el\(30^{\circ}-60^{\circ}-90^{\circ}\) triángulo y el\(45^{\circ}-45^{\circ}-90^{\circ}\) triángulo. El resto de los valores se obtuvieron de los ya conocidos mediante el uso de identidades trigonométricas y aproximación. Las identidades que utilizó fueron esencialmente las fórmulas de medio ángulo y suma y diferencia que los estudiantes encuentran en los cursos modernos de TrigonometrJ.
La trigonometría de los griegos, y más tarde de los hindúes y los árabes, se basó principalmente en la función sinusoidal. Los hindúes sustituyeron la tabla de acordes de Hiparco por una tabla de medios acordes. El término seno se deriva de una palabra hindú que significa “media cuerda”.
Poco a poco el triángulo rectángulo reemplazó los acordes de los círculos como base de las definiciones trigonométricas. El coseno es solo el seno del complemento del ángulo en un triángulo rectángulo, Por ejemplo el complemento de\(60^{\circ}\) es\(30^{\circ}\) y\(\cos 60^{\circ} = \sin 30^{\circ} = .5\).
Una tangente es una línea que toca un círculo en un solo punto (ver Capítulo 7). En trigonometría se refiere justamente a esa parte de la línea tangente interceptada por el ángulo, relativa al radio del círculo. En\(\PageIndex{2}\) la Figura la tangente de\(\angle DOE\) es el segmento\(DE\) dividido por el radio\(OD\). Los antiguos griegos eran probablemente conscientes de la función tangente pero la primera tabla de valores conocida fue construida por los árabes en el siglo X. El término “tangente” fue adoptado en el siglo XVI.
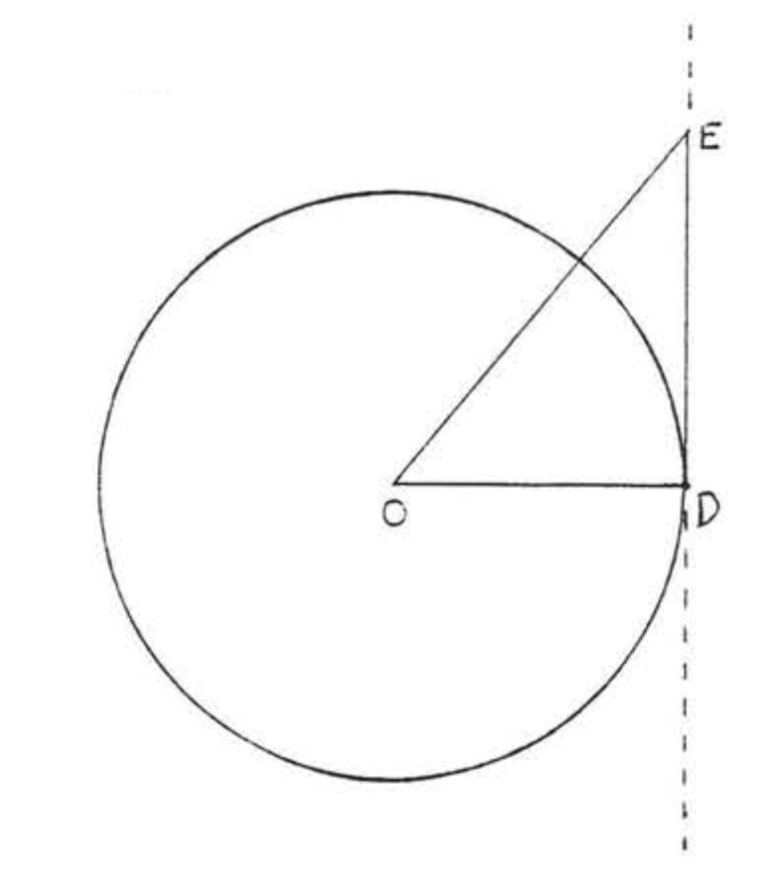
Las tablas trigonométricas modernas están construidas a partir de series infinitas. Estos fueron descubiertos por primera vez en el siglo XVII por Newton, Leibniz y otros. Por ejemplo, la serie infinita para la función sinusoidal es
\[\sin x = x - \dfrac{x^3}{6} + \dfrac{x^5}{120} - \dfrac{x^7}{5040} + \cdots\]
donde\(x\) está en radianes, 1 radián = 57.296 grados. Se puede obtener una buena aproximación del seno de un ángulo a partir de la serie infinita sumando solo las primeras diez centenas. Este es también el método que utilizan las computadoras y las calculadoras de bolsillo para encontrar valores trigonométricos. La derivación de estas fórmulas se encuentra en los libros de texto de cálculo.
Problemas
1 - 10. Encuentra cada uno de los siguientes usando la tabla:
1. \(\sin 10^{\circ}\)
2. \(\sin 30^{\circ}\)
3. \(\cos 80^{\circ}\)
4. \(\cos 60^{\circ}\)
5. \(\tan 45^{\circ}\)
6. \(\tan 60^{\circ}\)
7. \(\sin 18^{\circ}\)
8. \(\cos 72^{\circ}\)
9. \(\tan 50^{\circ}\)
10. \(\tan 80^{\circ}\)
11 - 30. Encuentra\(x\) a la décima más cercana:
11.
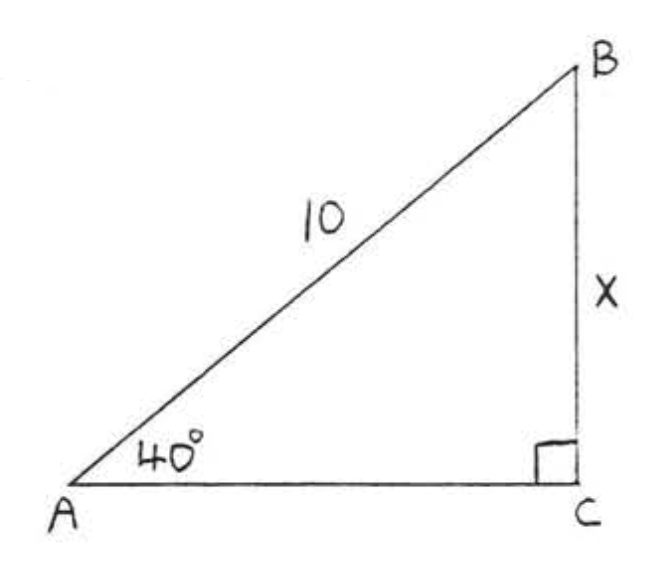
12.
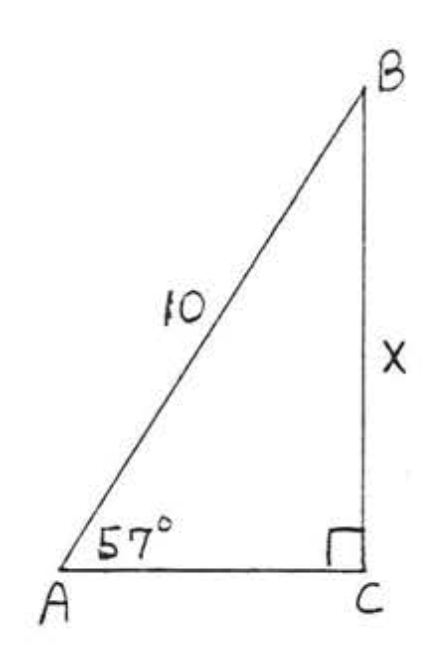
13.
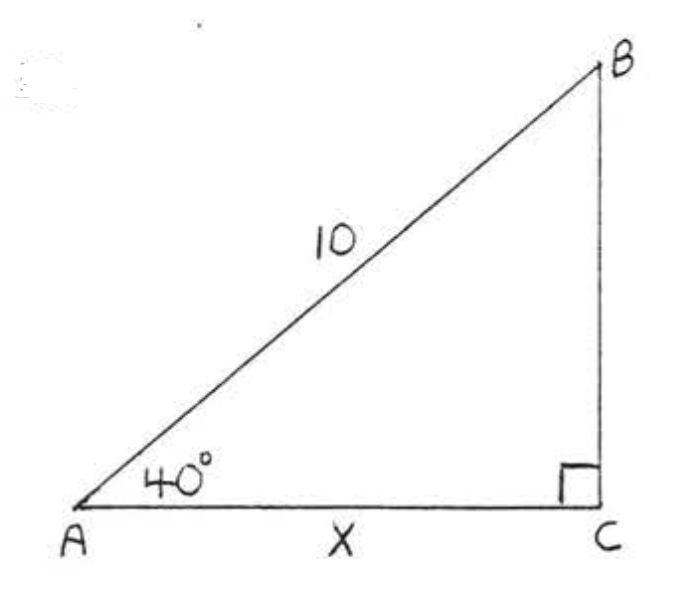
14.
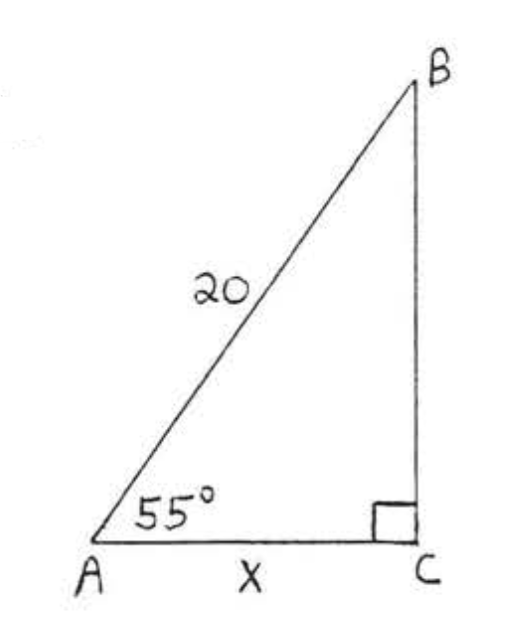
15.
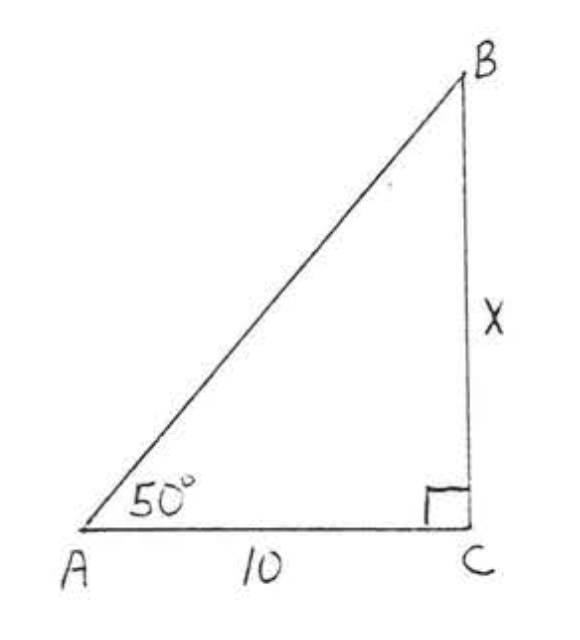
16.
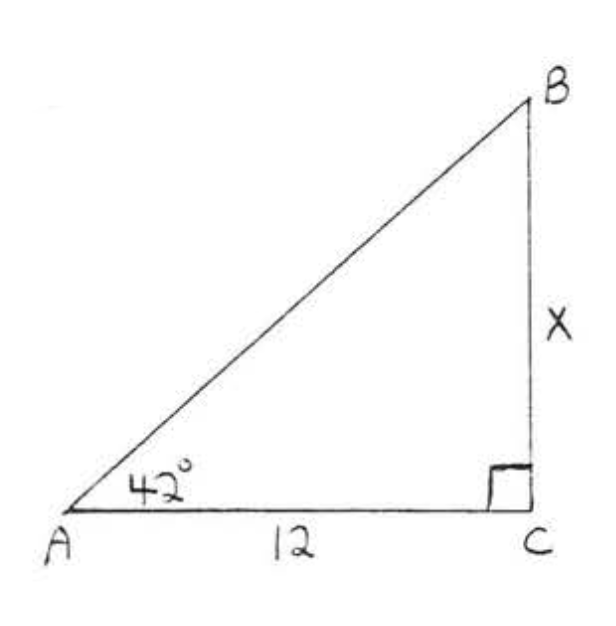
17.
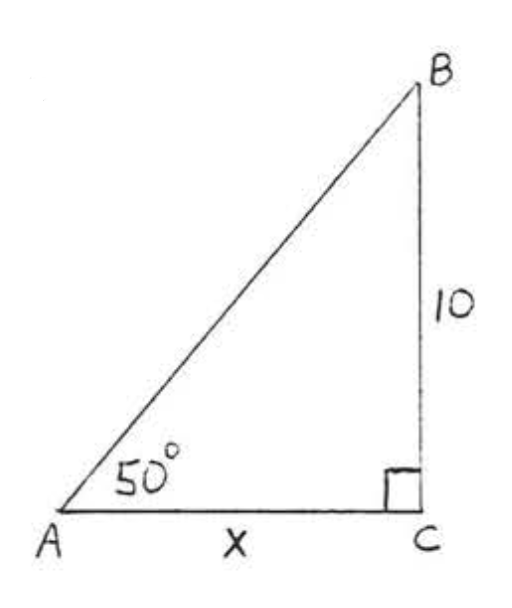
18.
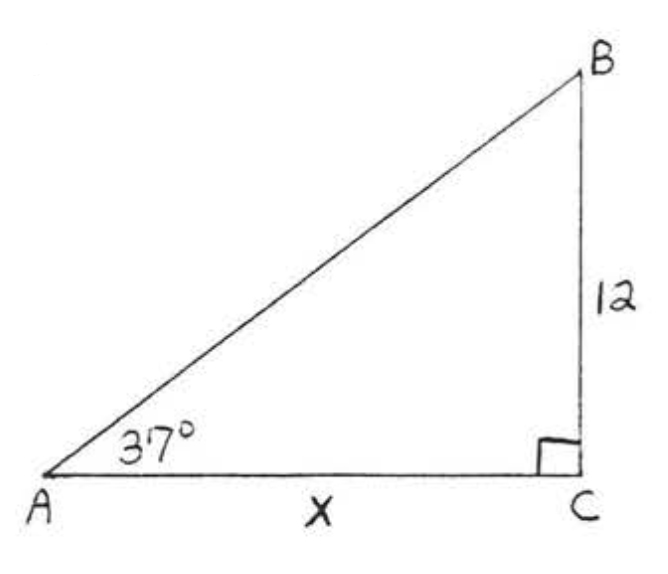
19.
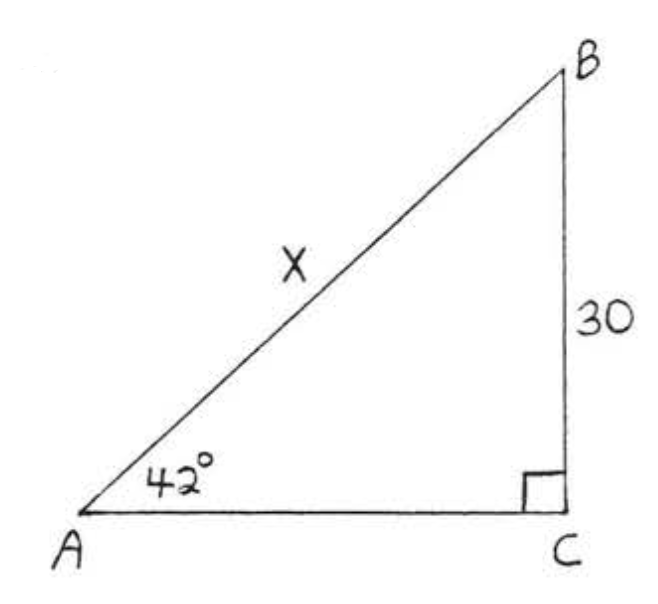
20.
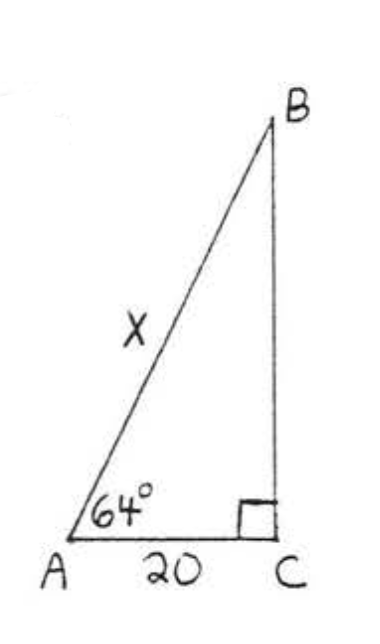
21.
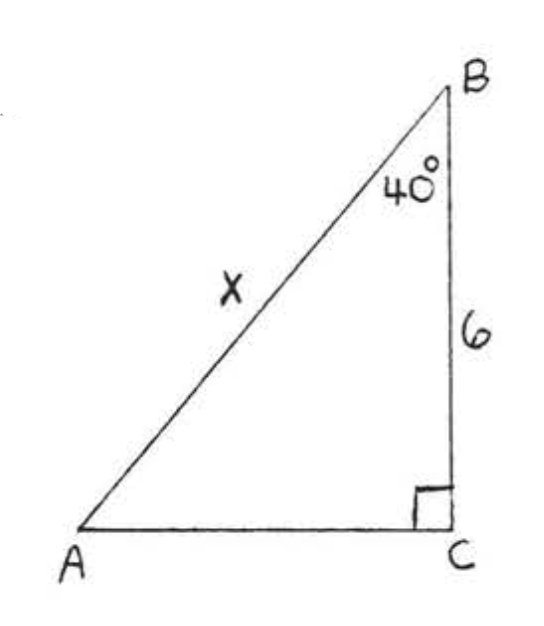
22.
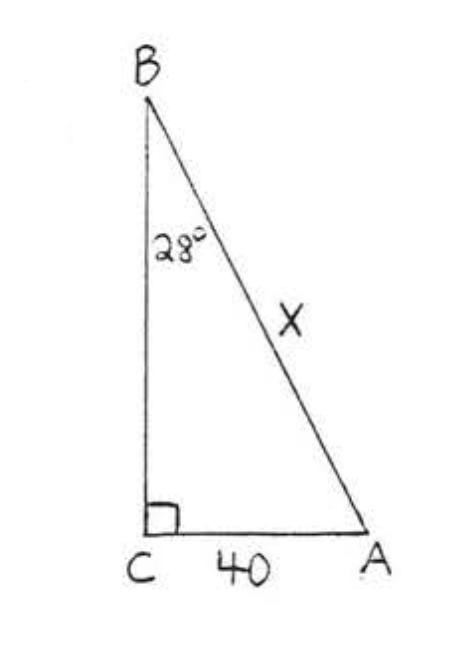
23.
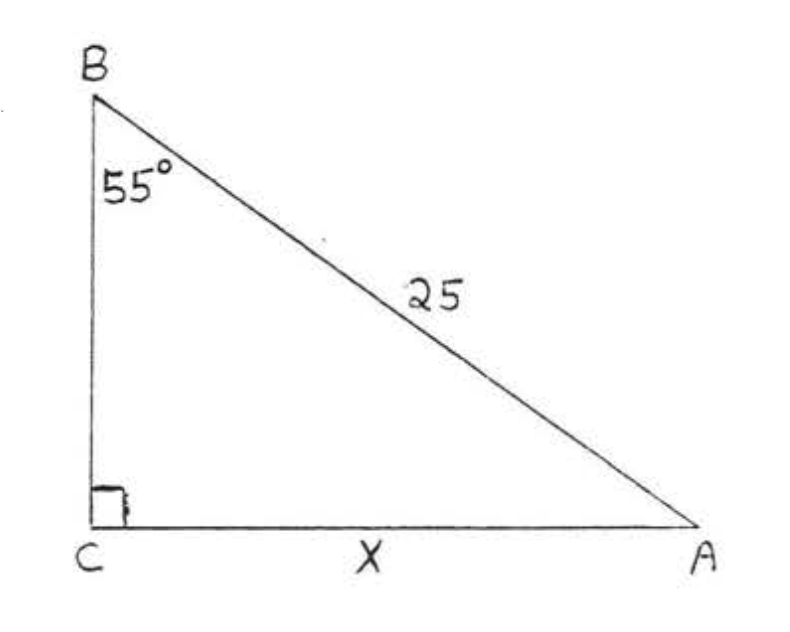
24.
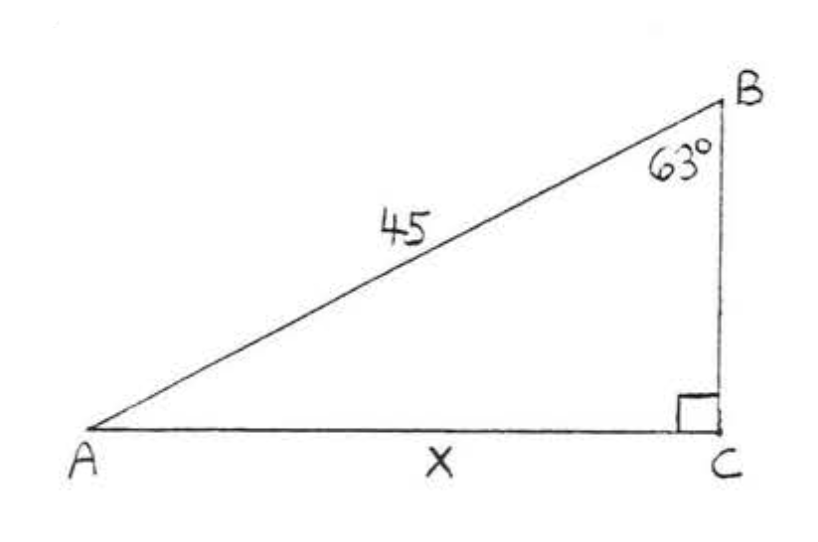
25.
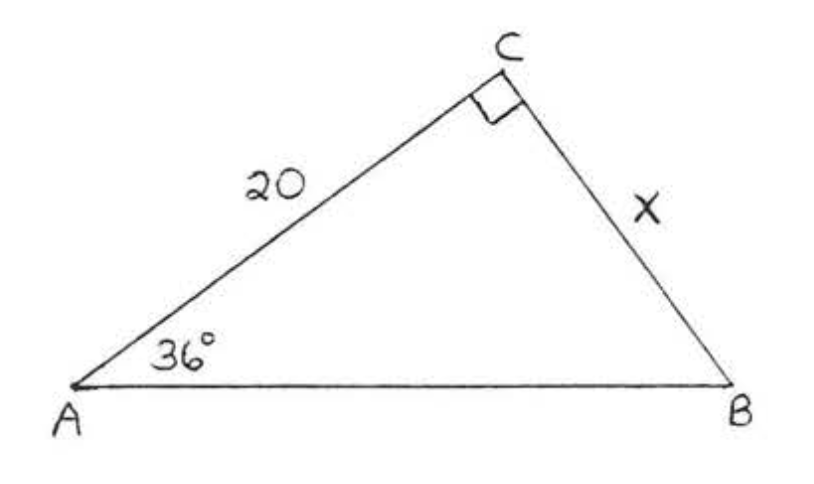
26.
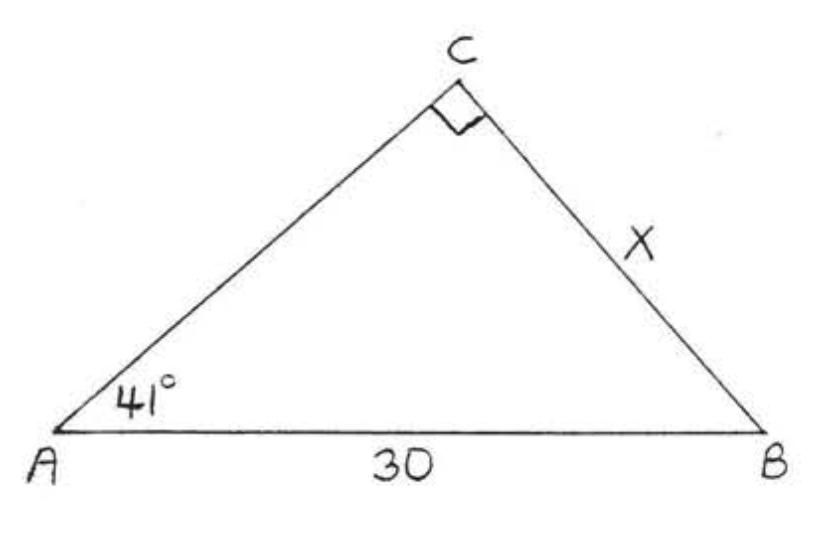
27.
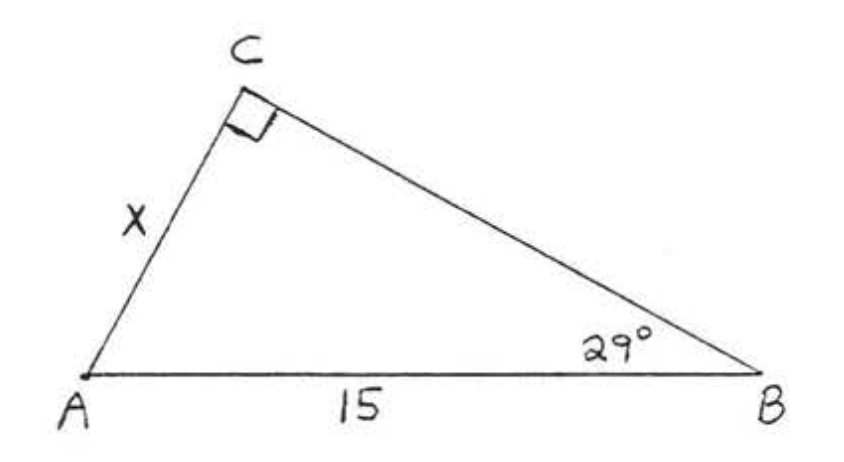
28.
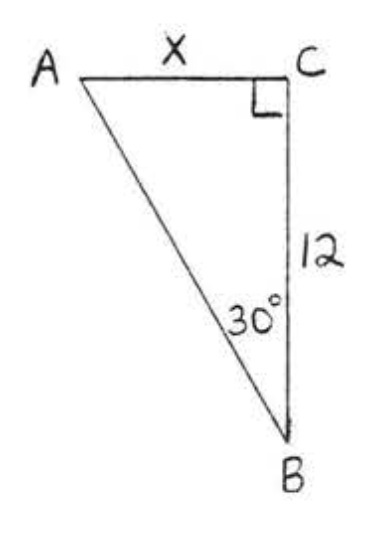
29.
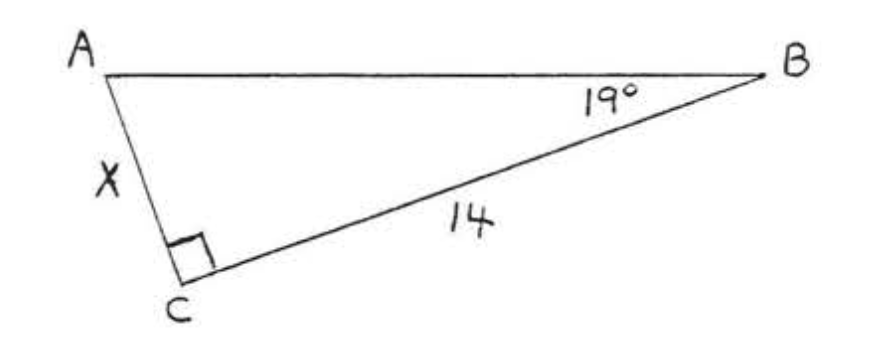
30.
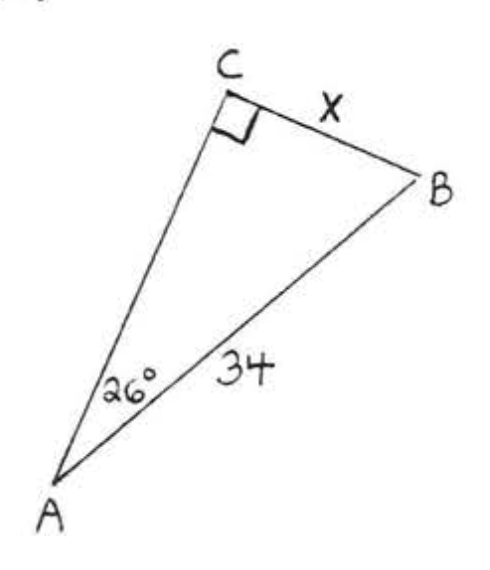
31 - 38. Encuentra\(x\) al grado más cercano:
31.
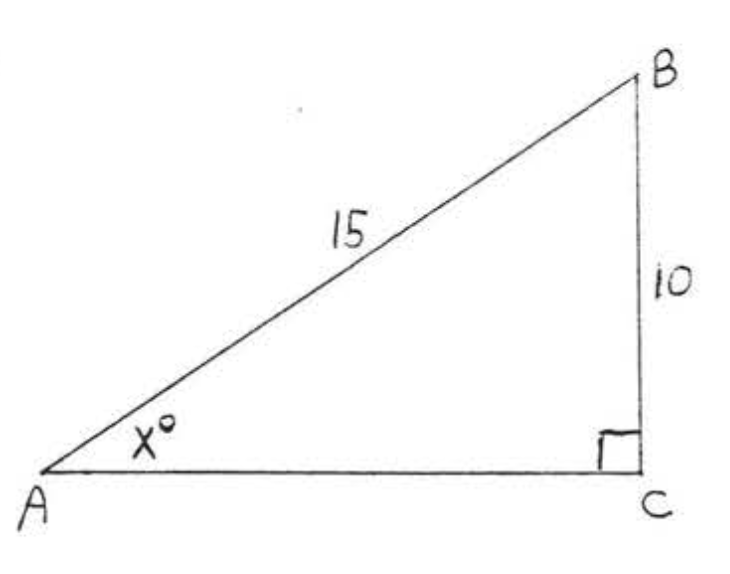
32.
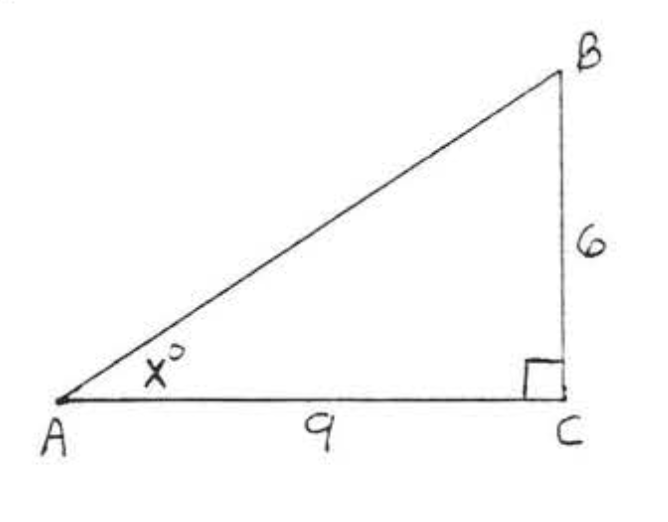
33.
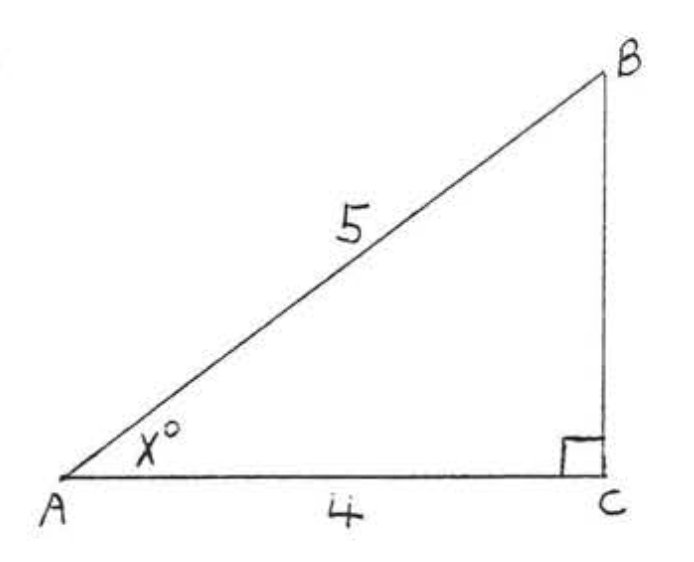
34.
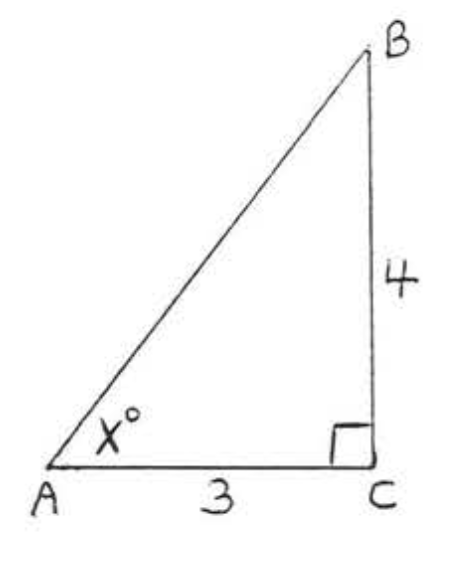
35.
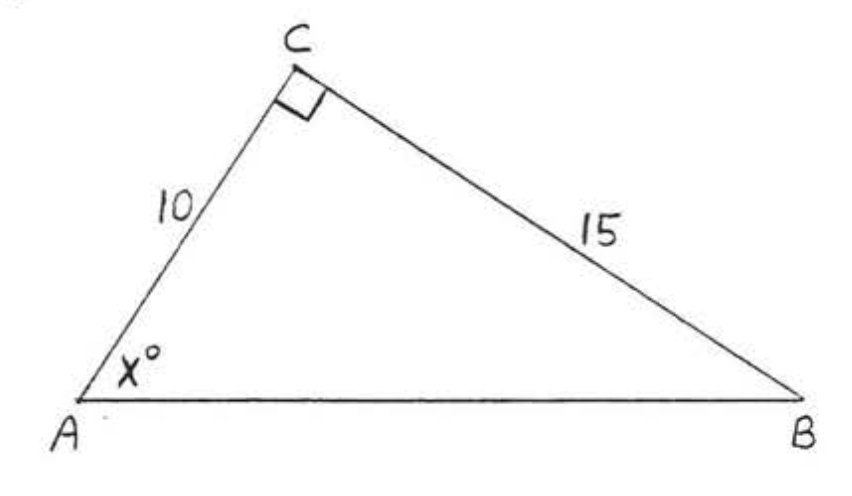
36.
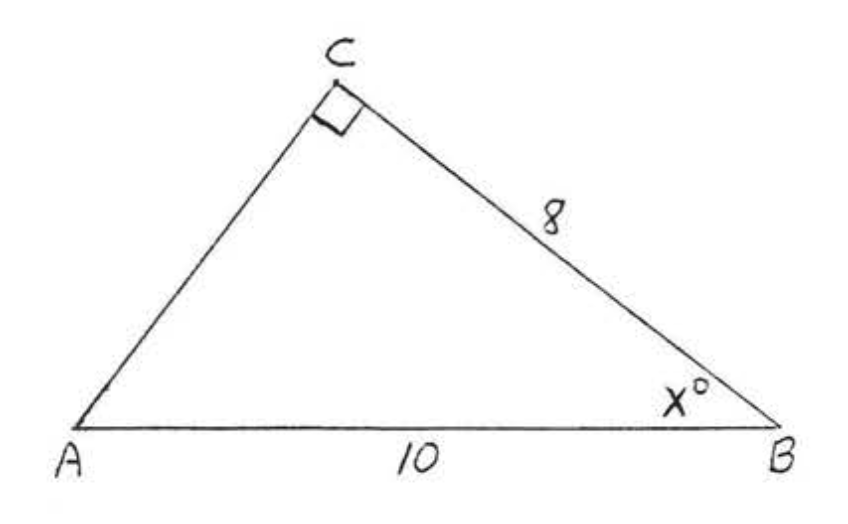
37.
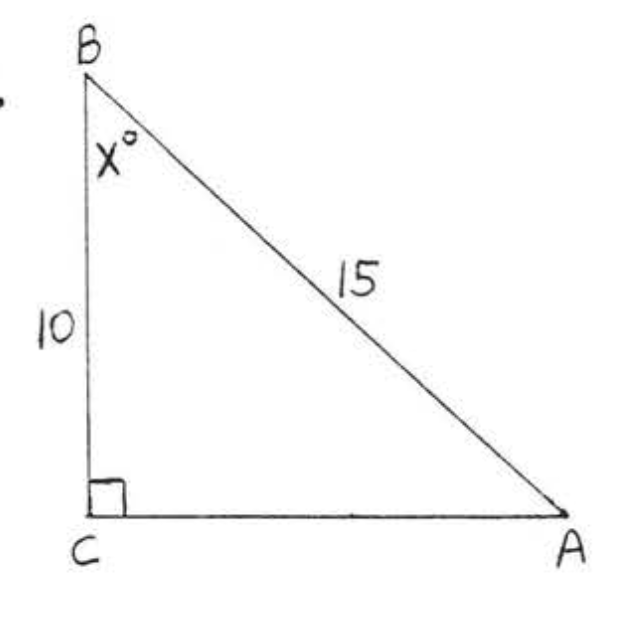
38.
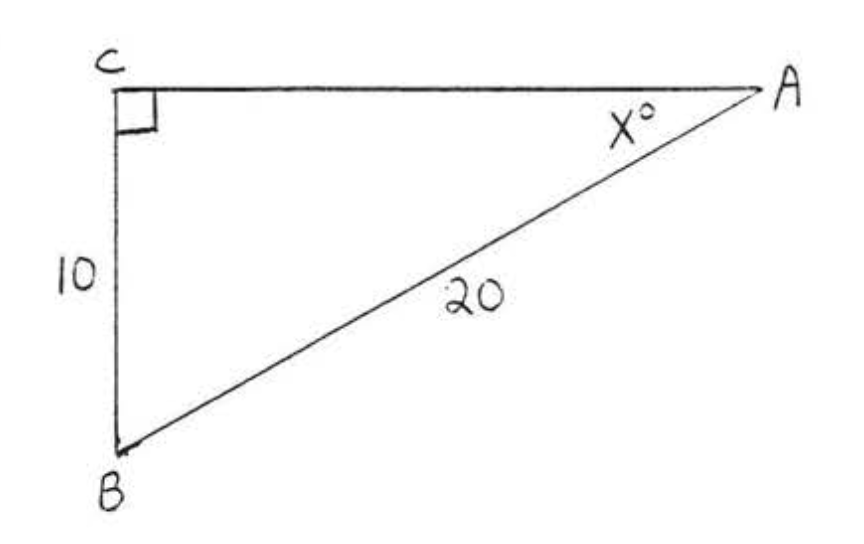
39 - 46. Encuentra\(x\) o\(x\) y\(y\) a la décima más cercana:
39.
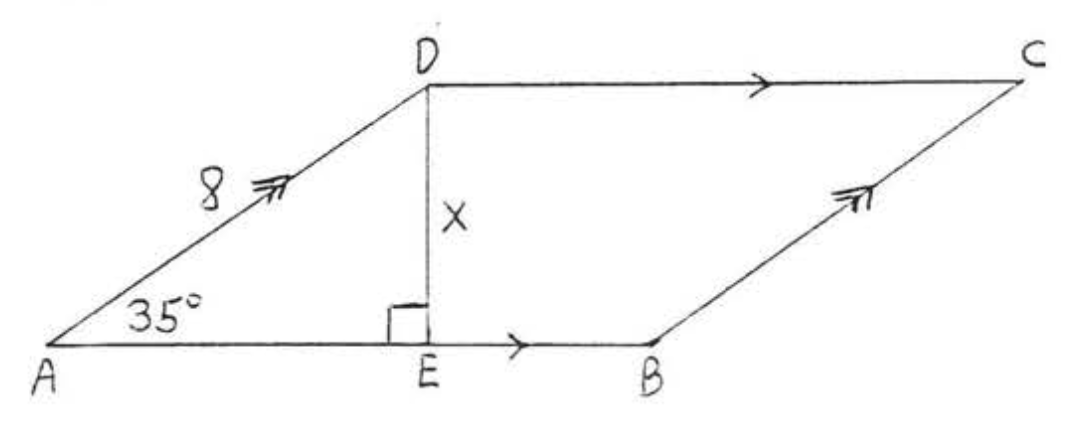
40.
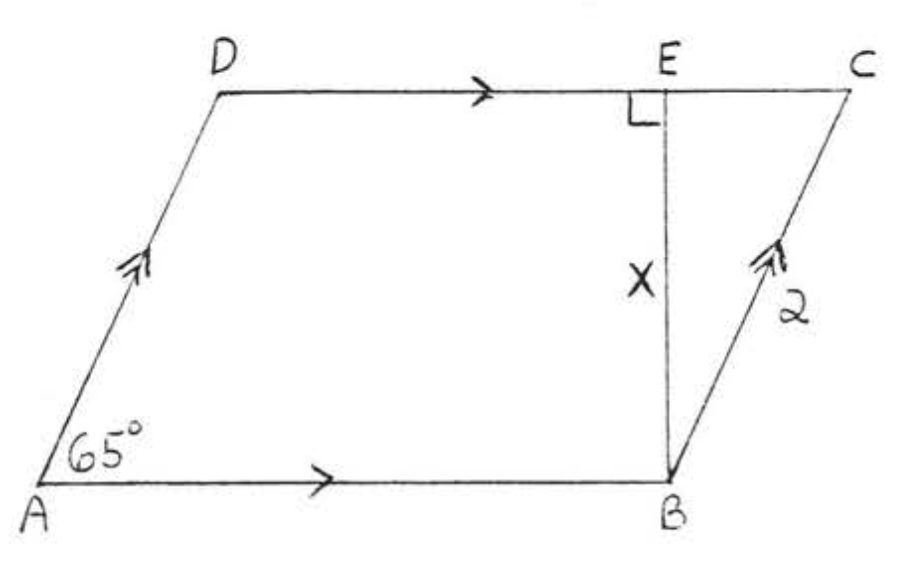
41.
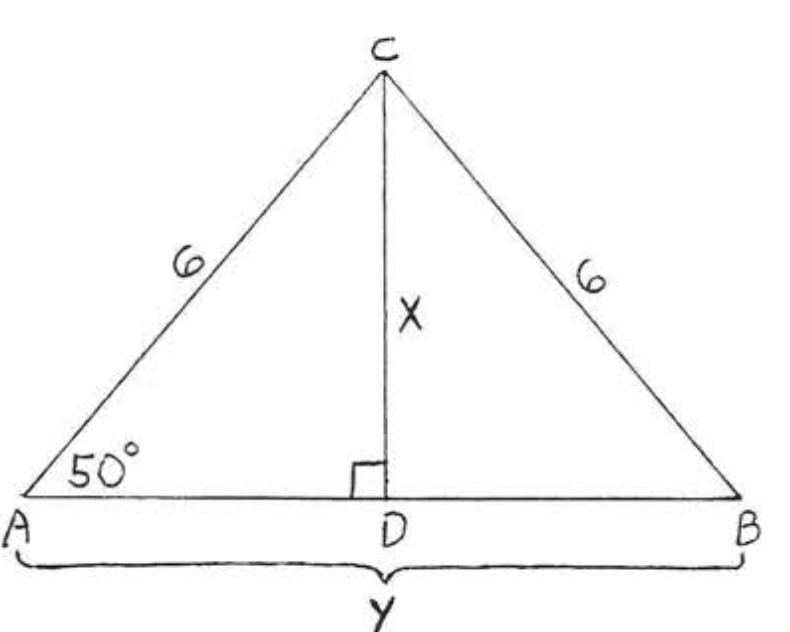
42.
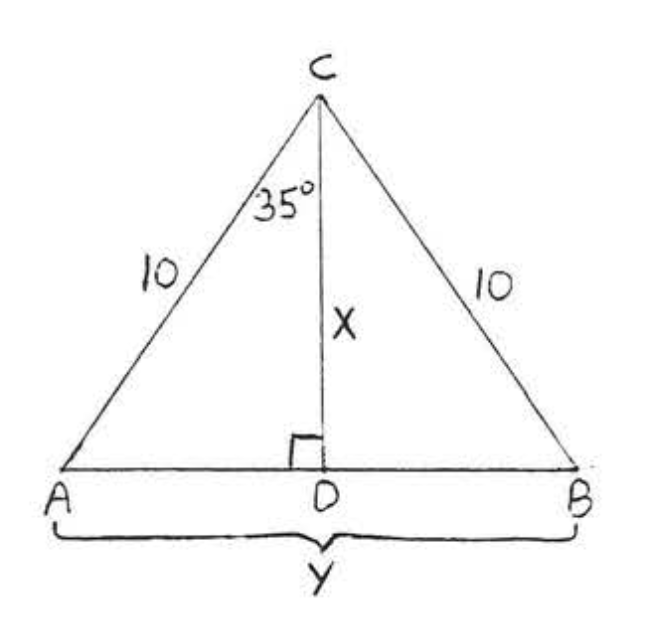
43.
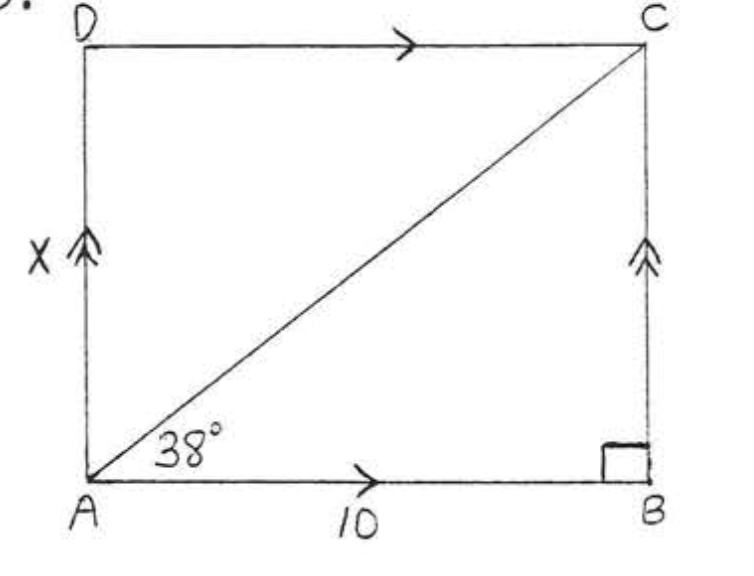
44.
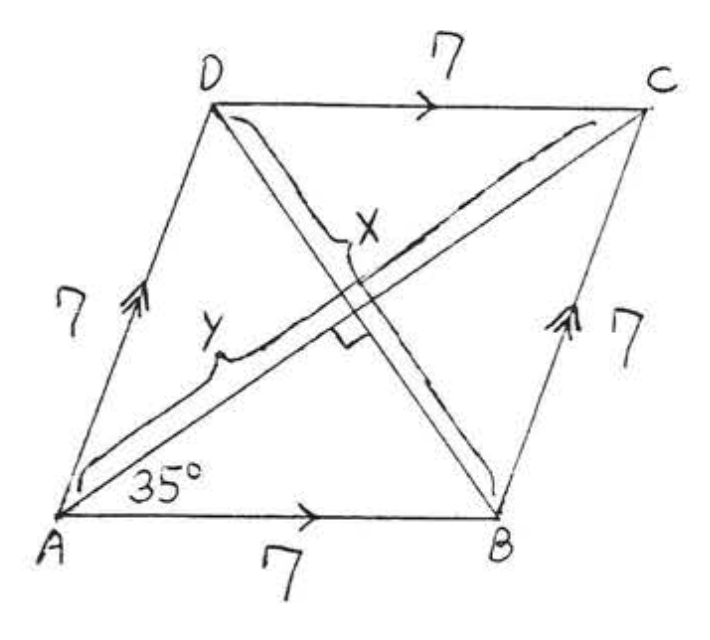
45.
46.
