4.1: Integrales de línea
- Page ID
- 111314
En el cálculo de una sola variable aprendiste a integrar una función de valor real a\(f (x)\) lo largo de un intervalo\([a,b]\) en\(\mathbb{R}^1\). Esta integral (generalmente llamada integral de Riemann) puede pensarse como una integral sobre un camino en\(\mathbb{R}^1\), ya que un intervalo (o colección de intervalos) es realmente el único tipo de “camino” en\(\mathbb{R}^1\). También puede recordar que si se\(f (x)\) representa la fuerza aplicada a lo largo del\(x\) eje a un objeto en la posición\(x\) en\([a,b]\), entonces el trabajo\(W\) realizado al mover ese objeto desde la posición\(x = a \text{ to }x = b\) se definió como la integral:
\[W=\int_a^b f (x)dx\]
En esta sección, veremos cómo definir la integral de una función (ya sea de valor real o vectorizado) de dos variables sobre una ruta general (es decir, una curva) en\(\mathbb{R}^2\). Esta definición estará motivada por la noción física de trabajo. Comenzaremos con funciones de valor real de dos variables.
En física, la idea intuitiva del trabajo es que
\[\text{Work = Force × Distance}\]
Supongamos que queremos encontrar la cantidad total\(W\) de trabajo realizado al mover un objeto a lo largo de una curva\(C\)\(\mathbb{R}^2\) con una parametrización suave\(x = x(t), y = y(t), a ≤ t ≤ b\), con una fuerza\(f (x, y)\) que varía con la posición\((x, y)\) del objeto y se aplica en la dirección del movimiento a lo largo de \(C\)(véase la Figura\(\PageIndex{1}\) a continuación).
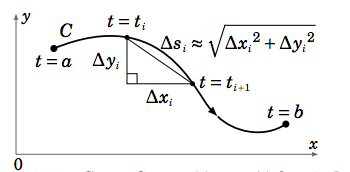
Asumiremos por ahora que la función\(f (x, y)\) es continua y de valor real, por lo que sólo consideramos la magnitud de la fuerza. Particionar el intervalo de\([a,b]\) la siguiente manera:
\[a = t_0 < t_1 < t_2 < ··· < t_{n−1} < t_n = b ,\text{ for some integer }n ≥ 2\]
Como podemos ver en la Figura\(\PageIndex{1}\), sobre un subintervalo típico\([t_i ,t_{i+1}]\) la distancia\(∆s_i\) recorrida a lo largo de la curva es aproximadamente\(\sqrt{∆x_i^2 +∆y_i^2}\), según el Teorema de Pitágoras. Así, si el subintervalo es lo suficientemente pequeño entonces el trabajo realizado para mover el objeto a lo largo de esa pieza de la curva es aproximadamente
\[\text{Force × Distance} \approx f (x_{i∗}, y_{i∗}) \sqrt{ ∆x_i^2 +∆y_i^2}\label{Eq4.1}\]
donde\((x_{i∗}, y_{i∗}) = (x(t_{i∗}), y(t_{i∗}))\) para algunos\(t_{i∗} \text{ in }[t_i ,t_{i+1}]\), y así
\[W \approx \sum_{i=0}^{n-1} f (x_{i∗}, y_{i∗}) \sqrt{ ∆x_i^2 +∆y_i^2}\label{Eq4.2}\]
es aproximadamente la cantidad total de trabajo realizado en toda la curva. Pero desde
\[\sqrt{ ∆x_i^2 +∆y_i^2} = \sqrt{\left ( \dfrac{∆x_i}{∆t_i} \right )^2 +\left ( \dfrac{∆y_i}{∆t_i}\right )^2}∆t_i\]
donde\(∆t_i = t_{i+1} − t_i\), entonces
\[W \approx \sum_{i=0}^{n-1}f (x_{i∗}, y_{i∗})\sqrt{\left ( \dfrac{∆x_i}{∆t_i} \right )^2 + \left ( \dfrac{∆y_i}{∆t_i} \right )^2}∆t_i \label{Eq4.3}\]
Tomando el límite de esa suma como la longitud del subintervalo más grande va a 0, la suma en todos los subintervalos se convierte en la integral de\(t = a \text{ to }t = b\), se\(∆x_i ∆t_i \text{ and }∆y_i ∆t_i\) convierte\(x ′ (t) \text{ and }y ′ (t)\), respectivamente, y\(f (x_{i∗}, y_{i∗})\) se convierte\(f (x(t), y(t))\), de manera que
\[W=\int_a^b f (x(t), y(t)) \sqrt{x ′ (t)^2 + y ′ (t)^2}\,dt \label{Eq4.4}\]
La integral en el lado derecho de la ecuación anterior nos da nuestra idea de cómo definir, para cualquier función de valor real\(f (x, y)\), la integral\(f (x, y)\) a lo largo de la curva\(C\), llamada integral de línea:
Definición\(\PageIndex{1}\): Line Integral of a scalar Field
Para una función de valor real\(f (x, y)\) y una curva\(C\) en\(\mathbb{R}^2\), parametrizada por\(x = x(t), y = y(t), a ≤ t ≤ b\), la integral de línea de\(f (x, y)\) lo largo\(C\) con respecto a la longitud del arco\(s\) es
\[\int_C f (x, y)\,ds = \int_a^b f (x(t), y(t))\sqrt{x ′ (t)^2 + y ′ (t)^2}\,dt \label{Eq4.5}\]
El símbolo\(ds\) es el diferencial de la función de longitud de arco
\[s = s(t) = \int_a^t \sqrt{x ′ (u)^2 + y ′ (u)^2}\,du \label{Eq4.6}\]
que puede reconocer de la Sección 1.9 como la longitud de la curva en el\(C\) intervalo\([a,t]\), para todos\(t\) en\([a,b]\). Es decir,
\[ds = s ′ (t)\,dt = \sqrt{x ′ (t)^2 + y ′ (t)^2}\,dt, \label{Eq4.7}\]
por el Teorema Fundamental del Cálculo.
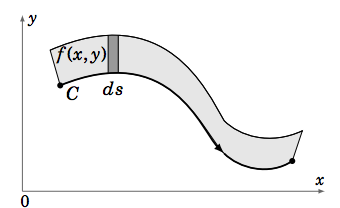
Para una función general de valor real\(f (x, y)\), ¿qué\(\int_C f (x, y)\,ds\) representa la integral de línea? La discusión anterior de nos\(ds\) da una pista. Se puede pensar en los diferenciales como longitudes infinitesimales. Entonces, si piensas en la altura de una cerca a lo largo de un piquete\(C\), entonces\(f (x, y)\,ds\) puede pensarse como aproximadamente el área de una sección de esa barda sobre alguna sección infinitesimalmente pequeña de la curva, y así la integral de línea\(\int_C f (x, y)\,ds\) es el área total de esa barda (ver Figura\(f (x, y)\) \(\PageIndex{2}\)).
Ejemplo\(\PageIndex{1}\)
Use una línea integral para mostrar que el área\(A\) de superficie lateral de un cilindro circular derecho de radio\(r\) y altura\(h\) es\(2\pi rh\).
Solución
Utilizaremos el cilindro circular derecho con círculo base\(C\) dado por\(x^2 + y^2 = r^2\) y con altura\(h\) en la\(z\) dirección positiva (ver Figura\(\PageIndex{3}\)). Parametrizar de\(C\) la siguiente manera:
\[x = x(t) = r \cos t , y = y(t) = r \sin t , 0 ≤ t ≤ 2π\]
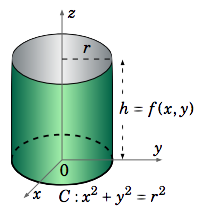
\[\nonumber \begin{align} A&=\int_C f (x, y)\,ds = \int_a^b f (x(t), y(t))\sqrt{x ′ (t)^2 + y ′ (t)^2}\,dt \\[4pt] \nonumber &=\int_0^{2\pi} h \sqrt{(−r \sin t)^2 +(r \cos t)^2}\,dt \\[4pt] \nonumber &=h\int_0^{2\pi} r \sqrt{\sin^2 t+\cos^2 t}\,dt \\[4pt] \nonumber &=rh\int_0^{2\pi} 1\,dt = 2\pi rh \\[4pt] \end{align}\]
Observe en Ejemplo\(\PageIndex{1}\) que si hubiéramos atravesado el círculo\(C\) dos veces, es decir, dejar que t varíe a partir de\(0 \text{ to }4\pi\) entonces habríamos obtenido un área de\(4\pi rh\), es decir, el doble del área deseada, aunque la curva en sí sigue siendo la misma (es decir, un círculo de radio\(r\)). Además, observe que atravesamos el círculo en sentido contrario a las agujas del reloj. Si hubiéramos ido en el sentido de las agujas del reloj, usando la parametrización
\[x = x(t) = r \cos (2π− t) , y = y(t) = r \sin (2π− t) , 0 ≤ t ≤ 2π ,\label{Eq4.8}\]
entonces es fácil verificar (Ejercicio 12) que el valor de la integral de línea no ha cambiado.
En general, se puede mostrar (Ejercicio 15) que invertir la dirección en la que\(C\) se recorre una curva deja\(\int_C f (x, y)\,ds\) sin cambios, para cualquiera\(f (x, y)\). Si una curva\(C\) tiene una parametrización\(x = x(t), y = y(t), a ≤ t ≤ b,\) entonces denota por\(−C\) la misma curva que\(C\) pero atravesada en la dirección opuesta. Luego\(−C\) se parametriza por
\[x = x(a+ b − t) , y = y(a+ b − t) , a ≤ t ≤ b ,\label{Eq4.9}\]
y tenemos
\[\int_C f (x, y)\,ds =\int_{-C}f (x, y)\,ds .\label{Eq4.10}\]
Observe que nuestra definición de la integral de línea fue con respecto al parámetro de longitud de arco\(s\). También podemos definir
\[\int_C f (x, y)\,dx=\int_a^b f (x(t), y(t)) x ′ (t)\,dt\label{Eq4.11}\]
como la línea integral de\(f (x, y)\) junto\(C\) con respecto a\(x\), y
\[\int_C f (x, y)\,d y=\int_a^b f (x(t), y(t)) y ′ (t)\,dt \label{Eq4.12}\]
como la línea integral de\(f (x, y)\) junto\(C\) con respecto a\(y\).
En la derivación de la fórmula para una integral lineal, se utilizó la idea de trabajo como fuerza multiplicada por distancia. No obstante, sabemos que la fuerza es en realidad un vector. Por lo que sería útil desarrollar una forma vectorial para una integral de línea. Para ello, supongamos que tenemos una función\(f(x, y)\) definida\(\mathbb{R}^2\) por
\[\nonumber \textbf{f}(x, y) = P(x, y)\textbf{i} + Q(x, y)\textbf{j}\]
para algunas funciones continuas de valor real\(P(x, y)\) y\(Q(x, y) \text{ on }\mathbb{R}^2\). Tal función\(f\) se llama un campo vectorial en\(\mathbb{R}^2\). Se define en puntos en\(\mathbb{R}^2\), y sus valores son vectores en\(\mathbb{R}^2\). Para una curva\(C\) con una parametrización suave\(x = x(t), y = y(t), a ≤ t ≤ b\), deje
\[\nonumber \textbf{r}(t) = x(t)\textbf{i} + y(t)\textbf{j}\]
ser el vector de posición para un punto\((x(t), y(t))\) encendido\(C\). Entonces\(\textbf{r}'(t) = x'(t)\textbf{i} + y'(t)\textbf{j}\) y así
\[\nonumber \begin{align} \int_C P(x, y)\,dx+ \int_C Q(x, y)\,d y &=\int_a^b P(x(t), y(t)) x ′ (t)\,dt+\int_a^b Q(x(t), y(t)) y ′ (t)\,dt \\[4pt] \nonumber &=\int_a^b (P(x(t), y(t)) x ′ (t)+Q(x(t), y(t)) y ′ (t))\,dt \\[4pt] \nonumber &=\int_a^b \textbf{f}(x(t), y(t))\cdot \textbf{r} ′ (t)dt \\[4pt] \end{align}\]
por definición de\(f(x, y)\). Observe que la función\(f(x(t), y(t))\cdot r ′ (t)\) es una función de valor real en\([a,b]\), por lo que la última integral de la derecha se ve algo similar a nuestra definición anterior de una integral de línea. Esto nos lleva a la siguiente definición:
Definición\(\PageIndex{2}\): Line Integral of a vector Field
Para un campo vectorial\(\textbf{f}(x, y) = P(x, y)\textbf{i} +Q(x, y)\textbf{j}\) y una curva\(C\) con una parametrización suave\(x = x(t), y = y(t), a ≤ t ≤ b\), la integral de línea de f a lo largo\(C\) es
\[\begin{align} \int_C \textbf{f}\cdot d\textbf{r} &= \int_C P(x, y)\,dx+\int_C Q(x, y)\,d y \label{Eq4.13} \\[4pt] &=\int_a^b \textbf{f}(x(t), y(t))\cdot \textbf{r} ′ (t)\,dt \label{Eq4.14} \\[4pt] \end{align}\]
donde\(\textbf{r}(t) = x(t)\textbf{i}+ y(t)\textbf{j}\) está el vector de posición para los puntos en\(C\).
Utilizamos la notación\(d\textbf{r} = \textbf{r} ′ (t)\,dt = dx\textbf{i}+ d y\textbf{j}\) para denotar el diferencial de la función valorada por vector r. La integral de línea en Definición a menudo\(\PageIndex{2}\) se denomina integral de línea de un campo vectorial para distinguirla de la integral de línea en Definición\(\PageIndex{1}\) que se llama integral de línea de un campo escalar. Para mayor comodidad, a menudo escribiremos
\[\nonumber \int_C P(x, y)\,dx +\int_C Q(x, y)\,d y =\int_C P(x, y)\,dx+Q(x, y)\,d y ,\]
donde se entiende que la línea integral a lo largo\(C\) se está aplicando a ambos\(P \text{ and }Q\). La cantidad\(P(x, y)\,dx +Q(x, y)\,d y\) se conoce como forma diferencial. Para una función de valor real\(F(x, y)\), el diferencial de\(F\) es
\[dF = \dfrac{∂F}{∂x}\,dx+ \dfrac{∂F}{∂y}\, d y.\]
Una forma diferencial\(P(x, y)\,dx+Q(x, y)\,d y\) se llama exacta si es igual\(dF\) para alguna función\(F(x, y)\).
Recordemos que si los puntos en una curva\(C\) tienen vector de posición\(\textbf{r}(t) = x(t)\textbf{i}+ y(t)\textbf{j}\), entonces\(\textbf{r} ′ (t)\) es un vector tangente\(C\) a en el punto\((x(t), y(t))\) en la dirección de incremento\(t\) (que llamamos la dirección de\(C\)). Dado que\(C\) es una curva suave, entonces\(\textbf{r} ′ (t) \neq \textbf{0} \text{ on }[a,b]\) y por lo tanto
\[\nonumber \textbf{T}(t) = \dfrac{\textbf{r}'(t)}{\left \lVert \textbf{r}'(t) \right \rVert} \]
es el vector tangente unitario a\(C\) at\((x(t), y(t))\). Poniendo Definiciones\(\PageIndex{1}\) y\(\PageIndex{2}\) juntos obtenemos el siguiente teorema:
Teorema\(\PageIndex{1}\)
Para un campo vectorial\(\textbf{f}(x, y) = P(x, y)\textbf{i} + Q(x, y)\textbf{j}\) y una curva\(C\) con un vector de parametrización\(x = x(t), y = y(t), a ≤ t ≤ b\) y posición suaves\(\textbf{r}(t) = x(t)\textbf{i}+ y(t)\textbf{j}\),
\[\int_C \textbf{f}\cdot d\textbf{r} = \int_C \textbf{f}\cdot \textbf{T}\,ds,\label{Eq4.15}\]
donde\(\textbf{T}(t) = \dfrac{\textbf{r} ′ (t)}{ \left \lVert \textbf{r} ′ (t)\right \rVert }\) es el vector tangente unitario a\(C\) at\((x(t), y(t))\).
Si el campo vectorial\( \textbf{f}(x, y)\) representa la fuerza que mueve un objeto a lo largo de una curva\(C\), entonces el trabajo\(W\) realizado por esta fuerza es
\[W = \int_C \textbf{f}\cdot \textbf{T} \, ds = \int_C \textbf{f}\cdot d\textbf{r} \label{Eq4.16}\]


