1.5: Funciones exponenciales y logarítmicas

Objetivos de aprendizaje

• Identificar la forma de una función exponencial.
• Explicar la diferencia entre las gráficas de$x^{b}$ y$b^{x}$.
• Reconocer la significación del número$e$.
• Identificar la forma de una función logarítmica.
• Explicar la relación entre funciones exponenciales y logarítmicas.
• Describir cómo calcular un logaritmo a una base diferente.
• Identificar las funciones hiperbólicas, sus gráficas e identidades básicas.

En esta sección examinamos las funciones exponenciales y logarítmicas. Utilizamos las propiedades de estas funciones para resolver ecuaciones que involucran términos exponenciales o logarítmicos, y estudiamos el significado y la importancia del número$e$. También definimos funciones hiperbólicas e hiperbólicas inversas, que involucran combinaciones de funciones exponenciales y logarítmicas. (Tenga en cuenta que presentamos definiciones alternativas de funciones exponenciales y logarítmicas en el capítulo Aplicaciones de Integraciones, y comprobamos que las funciones tienen las mismas propiedades con cualquiera de las definiciones.)

Funciones exponenciales

Las funciones exponenciales surgen en muchas aplicaciones. Un ejemplo común es el crecimiento poblacional. Por ejemplo, si una población comienza con$P_0$ individuos y luego crece a una tasa anual de$2\%$, su población después de 1 año es

$$P(1)=P_0+0.02P_0=P_0(1+0.02)=P_0(1.02).\nonumber$$

Su población después de 2 años es

$$P(2)=P(1)+0.02P(1)=P(1)(1.02)=P_0(1.02)^2.\nonumber$$

En general, su población después de$t$ años es

$$P(t)=P_0(1.02)^t,\nonumber$$

que es una función exponencial. De manera más general, cualquier función de la forma$f(x)=b^x$$b>0$, donde$b≠1$,, es una función exponencial con base$b$ y exponente Las funciones$x.$ exponenciales tienen bases constantes y exponentes variables. Tenga en cuenta que una función de la forma$f(x)=x^b$ para alguna constante no$b$ es una función exponencial sino una función de potencia.

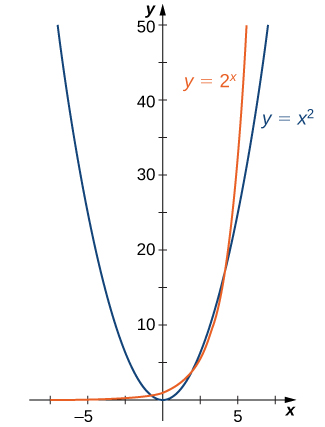
Para ver la diferencia entre una función exponencial y una función de potencia, comparamos las funciones$y=x^2$ y$y=2^x$. En Tabla$\PageIndex{1}$, vemos que tanto$2^x$ y se$x^2$ acercan al infinito como$x→∞$. Eventualmente, sin embargo,$2^x$ se vuelve más grande que$x^2$ y crece más rápidamente a medida que$x→∞$. En sentido contrario, como$x→−∞$,$x^2→∞$, mientras$2^x→0$. La línea$y=0$ es una asíntota horizontal para$y=2^x$.

Mesa$\PageIndex{1}$

$x$	-3	-2	-1	0	1	2	3	4	5	6
$x^2$	9	4	1	0	1	4	9	16	25	36
$2^x$	1/8	1/4	1/2	1	2	4	8	16	32	64

En la Figura$\PageIndex{1}$, graficamos ambos$y=x^2$ y$y=2^x$ para mostrar en qué se diferencian las gráficas.

Figura$\PageIndex{1}$: Ambos$2^x$ y$x^2$ acercarse al infinito como$x→∞$, pero$2^x$ crece más rápidamente que$x^2$. Como$x→−∞$,$x^2→∞$, mientras que$2^x→0$.

Evaluación de funciones exponenciales

Recordemos las propiedades de los exponentes: Si$x$ es un entero positivo, entonces definimos$b^x=b⋅b⋯b$ (con$x$ factores de$b$). Si$x$ es un entero negativo, entonces$x=−y$ para algún entero positivo$y$, y definimos$b^x=b^{−y}=1/b^y$. También,$b^0$ se define como que sea$1$. Si$x$ es un número racional, entonces$x=p/q$, donde$p$ y$q$ son enteros y$b^x=b^{p/q}=\sqrt[q]{b^p}$. Por ejemplo,$9^{3/2}=\sqrt{9^3}=\left(\sqrt{9}\right)^3=27$. Sin embargo, ¿cómo se$b^x$ define si$x$ es un número irracional? Por ejemplo, ¿a qué nos referimos con$2^{\sqrt{2}}$? Esta es una pregunta demasiado compleja para que podamos responder plenamente ahora mismo; sin embargo, podemos hacer una aproximación.

Tabla$\PageIndex{2}$: Valores de$2^x$ para una lista de números racionales aproximados$\sqrt{2}$

$x$	1.4	1.41	1.414	1.4142	1.41421	1.414213
$2^x$	2.639	2.65737	2.66475	2.665119	2.665138	2.665143

En Tabla$\PageIndex{2}$, enumeramos algunos números racionales que se aproximan$\sqrt{2}$, y también$x$ se presentan los valores de$2^x$ para cada número racional. Afirmamos que si elegimos números racionales$x$ cada vez más cerca$\sqrt{2}$, los valores de cada vez se$2^x$ acercan más a algún número$L$. Definimos ese número$L$ para que sea$2^{\sqrt{2}}$.

Ejemplo$\PageIndex{1}$: Bacterial Growth

Supongamos que se sabe que una población particular de bacterias se duplica en tamaño cada$4$ hora. Si un cultivo comienza con$1000$ bacterias, el número de bacterias después de$4$ horas es$n(4)=1000⋅2$. El número de bacterias después de$8$ horas es$n(8)=n(4)⋅2=1000⋅2^2$. En general, el número de bacterias después de$4m$ horas es$n(4m)=1000⋅2^m$. Dejando$t=4m$, vemos que el número de bacterias después de t horas es$n(t)=1000⋅2^{t/4}$. Encuentra el número de bacterias después de$6$$10$ horas, horas y$24$ horas.

Solución

El número de bacterias después de 6 horas viene dado por

$$n(6)=1000⋅2^{6/4}≈2828\, \text{bacteria}. \nonumber$$

El número de bacterias después de$10$ horas viene dado por

$$n(10)=1000⋅2^{10/4}≈5657\, \text{bacteria}. \nonumber$$

El número de bacterias después del$24$ horario es dado por$n(24)=1000⋅2^6=64,000$ bacterias.

Ejercicio$\PageIndex{1}$

Dada la función exponencial$f(x)=100⋅3^{x/2}$, evaluar$f(4)$ y$f(10)$.

Contestar

$f(4)=900$

$f(10)=24,300$.

Graficando Funciones Exponenciales

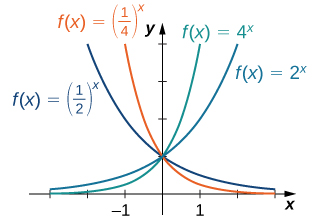
Para cualquier base$b>0$,$b≠1$, la función exponencial$f(x)=b^x$ se define para todos los números reales$x$ y$b^x>0$. Por lo tanto, el dominio de$f(x)=b^x$ es$(−∞,∞)$ y el rango es$(0,∞)$. Para graficar$b^x$, observamos que para$b>1$,$b^x$ va aumentando en$(−∞,∞)$ y$b^x→∞$ como$x→∞$, mientras que$b^x→0$ as$x→−∞$. Por otro lado, si$0<b<1$,$f(x)=b^x$ es decreciente sobre$(−∞,∞)$ y$b^x→0$ como$x→∞$ mientras$b^x→∞$ como$x→−∞$ (Figura$\PageIndex{2}$).

Figura$\PageIndex{2}$: Si$b>1$, entonces$b^x$ está aumentando en$(−∞,∞)$. Si$0<b<1$, entonces$b^x$ está disminuyendo en$(−∞,∞)$.

Tenga en cuenta que las funciones exponenciales satisfacen las leyes generales de los exponentes. Para recordarte estas leyes, las declaramos como reglas.

Leyes de los exponentes

Para cualquier constante$a>0$,$b>0$, y para todos$x$ y$y,$

1. $$b^x⋅b^y=b^{x+y} \nonumber$$
2. $$\dfrac{b^x}{b^y}=b^{x−y} \nonumber$$
3. $$(b^x)^y=b^{xy} \nonumber$$
4. $$(ab)^x=a^xb^x \nonumber$$
5. $$\dfrac{a^x}{b^x}=\left(\dfrac{a}{b}\right)^x \nonumber$$

Ejemplo$\PageIndex{2}$: Using the Laws of Exponents

Utilice las leyes de los exponentes para simplificar cada una de las siguientes expresiones.

1. $\dfrac{(2x^{2/3})^3}{(4x^{−1/3})^2}$
2. $\dfrac{(x^3y^{−1})^2}{(xy^2)^{−2}}$

Soution

a. Podemos simplificar de la siguiente manera:

$$\dfrac{(2x^{2/3})^3}{(4x^{−1/3})^2}=\dfrac{2^3(x^{2/3})^3}{4^2(x^{−1/3})^2}= \dfrac{8x^2}{16x^{−2/3}} =\dfrac{x^2x^{2/3}}{2}=\dfrac{x^{8/3}}{2}. \nonumber$$

b. Podemos simplificar de la siguiente manera:

$$\dfrac{(x^3y^{−1})^2}{(xy^2)^{−2}}=\dfrac{(x^3)^2(y^{−1})^2}{x^{−2}(y^2)^{−2}}=\dfrac{x^6y^{−2}}{x^{−2}y^{−4}} =x^6x^2y^{−2}y^4=x^8y^2. \nonumber$$

Ejercicio$\PageIndex{2}$

Utilice las leyes de los exponentes para simplificar$\dfrac{6x^{−3}y^2}{12x^{−4}y^5}$.

Pista

$x^a/x^b=x^{a-b}$

Contestar

$x/(2y^3)$

El número e

Un tipo especial de función exponencial aparece frecuentemente en aplicaciones del mundo real. Para describirlo, considere el siguiente ejemplo de crecimiento exponencial, que surge del interés compuesto en una cuenta de ahorro. Supongamos que una persona invierte$P$ dólares en una cuenta de ahorro con una tasa de interés anual$r$, agravada anualmente. La cantidad de dinero después de 1 año es

$A(1)=P+rP=P(1+r)$.

La cantidad de dinero después de$2$ años es

$A(2)=A(1)+rA(1)=P(1+r)+rP(1+r)=P(1+r)^2$.

De manera más general, la cantidad después de$t$ años es

$A(t)=P(1+r)^t$.

Si el dinero se compone 2 veces al año, la cantidad de dinero después de medio año es

$A\left(\dfrac{1}{2}\right)=P+\left(\dfrac{r}{2}\right)P=P\left(1+\left(\dfrac{r}{2}\right)\right)$.

La cantidad de dinero tras$1$ año es

$A(1)=A\left(\dfrac{1}{2}\right)+\left(\dfrac{r}{2}\right)A \left(\dfrac{1}{2}\right)=P\left(1+\dfrac{r}{2}\right)+\dfrac{r}{2}\left(\left(P(1+\dfrac{r}{2}\right)\right)=P\left(1+\dfrac{r}{2}\right)^2.$

Después de$t$ años, la cantidad de dinero en la cuenta es

$A(t)=P\left(1+\dfrac{r}{2}\right)^{2t}$.

De manera más general, si el dinero se compone$n$ veces al año, la cantidad de dinero en la cuenta después de$t$ años viene dada por la función

$A(t)=P\left(1+\dfrac{r}{n}\right)^{nt}.$

Qué pasa como$n→∞?$ Para responder a esta pregunta, dejamos$m=n/r$ y escribimos

$\left(1+\dfrac{r}{n}\right)^{nt}=\left(1+\dfrac{1}{m}\right)^{mrt},$

y examinar el comportamiento de$(1+1/m)^m$ as$m→∞$, utilizando una tabla de valores (Tabla$\PageIndex{3}$).

Tabla$\PageIndex{3}$: Valores de$\left(1+\dfrac{1}{m}\right)^m$ as$m→∞$

$m$	10	100	1000	10,000	100,000	1,000,000
$\left(1+\dfrac{1}{m}\right)^m$	2.5937	2.7048	2.71692	2.71815	2.718268	2.718280

Al mirar esta mesa, parece que$(1+1/m)^m$ se está acercando a un número entre$2.7$ y$2.8$ como$m→∞$. De hecho,$(1+1/m)^m$ sí se acerca a algún número como$m→∞$. Llamamos a este número$e$. A seis decimales de precisión,

$$e≈2.718282. \nonumber$$

Leonhard Euler

La letra$e$ fue utilizada por primera vez para representar este número por el matemático suizo Leonhard Euler durante la década de 1720. Aunque Euler no descubrió el número, mostró muchas conexiones importantes entre$e$ y funciones logarítmicas. Todavía usamos la notación$e$ hoy en día para honrar el trabajo de Euler porque aparece en muchas áreas de las matemáticas y porque podemos usarlo en muchas aplicaciones prácticas.

Volviendo a nuestro ejemplo de cuenta de ahorro, podemos concluir que si una persona pone$P$ dólares en una cuenta a una tasa de interés anual$r$, agravada continuamente, entonces$A(t)=Pe^{rt}$. Esta función puede ser familiar. Dado que las funciones que involucran base$e$ surgen a menudo en las aplicaciones, llamamos a$f(x)=e^x$ la función la función exponencial natural. Esta función no sólo es interesante por la definición del número$e$, sino que también, como se discutirá a continuación, su gráfica tiene una propiedad importante.

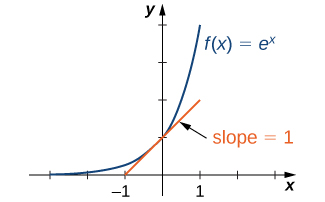
Ya que$e>1$, sabemos que$f(x) = e^x$ va en aumento$(−∞,∞)$. En la Figura$\PageIndex{3}$, se muestra una gráfica de$f(x)=e^x$ junto con una línea tangente a la gráfica de$f$ at$x=0$. Damos una definición precisa de línea tangente en el siguiente capítulo; pero, informalmente, decimos que una línea tangente a una gráfica de$f$ at$x=a$ es una línea que pasa por el punto$(a,f(a))$ y tiene la misma “pendiente” que$f$ en ese punto. La función$f(x)=e^x$ es la única función exponencial$b^x$ con línea tangente en la$x=0$ que tiene una pendiente de$1.$ Como vemos más adelante en el texto, tener esta propiedad hace que la función exponencial natural sea la función exponencial más simple de usar en muchas instancias.

Figura$\PageIndex{3}$: La gráfica de$f(x)=e^x$ tiene una línea tangente con pendiente$1$ en$x=0$.

Ejemplo$\PageIndex{3}$: Compounding Interest

Supongamos que$$500$ se invierte en una cuenta a una tasa de interés anual de$r=5.5\%$, compuesto continuamente.

1. Dejar$t$ denotar el número de años después de la inversión inicial y$A(t)$ denotar la cantidad de dinero en la cuenta en el momento$t$. Encuentra una fórmula para$A(t)$.
2. Encuentra la cantidad de dinero en la cuenta después de$10$ años y después de$20$ años.

Solución

a. si los$P$ dólares se invierten en una cuenta a una tasa de interés anual$r$, agravada continuamente, entonces$A(t)=Pe^{rt}$. Aquí$P=$500$ y$r=0.055$. Por lo tanto,$A(t)=500e^{0.055t}$.

b. Después de$10$ años, la cantidad de dinero en la cuenta es

$A(10)=500e^{0.055⋅10}=500e^{0.55}≈$866.63$.

Después de$20$ años, la cantidad de dinero en la cuenta es

$A(20)=500e^{0.055⋅20}=500e^{1.1}≈$1,502.08$.

Ejercicio$\PageIndex{3}$

Si$$750$ se invierte en una cuenta a una tasa de interés anual de$4\%$, compuesto continuamente, encuentre una fórmula para la cantidad de dinero en la cuenta después de$t$ años. Encuentra la cantidad de dinero después de$30$ años.

Pista

$A(t)=Pe^{rt}$

Contestar

$A(t)=750e^{0.04t}$. Después de$30$ años, habrá aproximadamente$$2,490.09$.

Funciones logarítmicas

Usando nuestra comprensión de las funciones exponenciales, podemos discutir sus inversos, que son las funciones logarítmicas. Estos son útiles cuando necesitamos considerar cualquier fenómeno que varíe en un amplio rango de valores, como la escala de pH en química o decibelios en los niveles de sonido.

La función exponencial$f(x)=b^x$ es uno a uno, con dominio$(−∞,∞)$ y rango$(0,∞)$. Por lo tanto, tiene una función inversa, llamada la función logarítmica con base$b$. Para cualquiera$b>0,\, b≠1$, la función logarítmica con base$b$, denotada$\log_b$, tiene dominio$(0,∞)$ y rango$(−∞,∞)$, y satisface

$$\log_b(x)=y \nonumber$$

si y sólo si$b^y=x$.

Por ejemplo,

$$\log_2(8)=3\nonumber$$

ya que$2^3=8$,

$$\log_{10}\left(\dfrac{1}{100}\right)=−2 \nonumber$$

ya que$10^{−2}=\dfrac{1}{10^2}=\dfrac{1}{100}$,

$$\log_b(1)=0 \nonumber$$

ya que$b^0=1$ para cualquier base$b>0$.

Además, dado que$y=\log_b(x)$ y$y=b^x$ son funciones inversas,

$$\log_b(b^x)=x \nonumber$$

y

$$b^{\log_b(x)}=x. \nonumber$$

La función logarítmica más utilizada es la función$\log_e$. Dado que esta función utiliza natural$e$ como base, se le llama logaritmo natural. Aquí usamos la notación$\ln (x)$ o$\ln x$ para significar$\log_e(x)$. Por ejemplo,

$$\begin{align*} \ln (e) &=\log_e(e)=1 \\[4pt] \ln (e^3) &=\log_e(e^3)=3 \\[4pt] \ln (1) &=\log_e(1)=0. \end{align*}$$

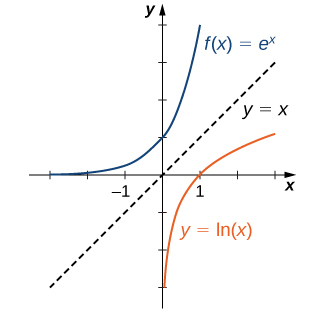
Dado que las funciones$f(x)=e^x$ y$g(x)=\ln (x)$ son inversas unas de otras,

$\ln (e^x)=x$y$e^{\ln x}=x$,

y sus gráficas son simétricas sobre la línea$y=x$ (Figura$\PageIndex{4}$).

Figura$\PageIndex{4}$: Las funciones$y=e^x$ y$y=\ln (x)$ son inversas entre sí, por lo que sus gráficas son simétricas alrededor de la línea$y=x$.

En general, para cualquier base$b>0$,$b≠1$, la función$g(x)=\log_b(x)$ es simétrica sobre la línea$y=x$ con la función$f(x)=b^x$. Usando este hecho y las gráficas de las funciones exponenciales, graficamos funciones$\log_b$ para varios valores de$b>1$ (Figura$\PageIndex{5}$).

Figura$\PageIndex{5}$: Las gráficas de$y=\log_b(x)$ se representan para$b=2,\,e,\,10$.

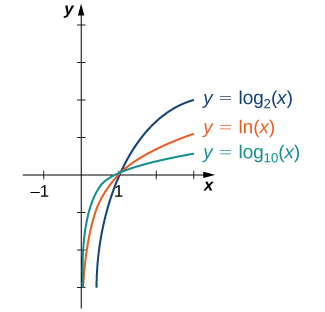
Antes de resolver algunas ecuaciones que involucran funciones exponenciales y logarítmicas, revisemos las propiedades básicas de los logaritmos.

Propiedades de logaritmos

Si$a,\,b,\,c>0,\,b≠1$, y$r$ es cualquier número real, entonces

• Propiedad del producto

$$\log_b(ac)=\log_b(a)+\log_b(c) \label{productprop}$$

• Propiedad del cociente

$$\log_b \left(\dfrac{a}{c} \right)=\log_b(a)−\log_b(c) \label{quotientprop}$$

• Propiedad de energía

$$\log_b(a^r)=r\log_b(a) \label{powerprop}$$

Ejemplo$\PageIndex{4}$: Solving Equations Involving Exponential Functions

Resuelve cada una de las siguientes ecuaciones para$x$.

1. $5^x=2$
2. $e^x+6e^{−x}=5$

Solución

a. Aplicando la función de logaritmo natural a ambos lados de la ecuación, tenemos

$\ln 5^x=\ln 2$.

Usando la propiedad de poder de logaritmos,

$x\ln 5=\ln 2.$

Por lo tanto,

$$x= \dfrac{\ln 2}{\ln 5}. \nonumber$$

b. Multiplicando ambos lados de la ecuación por$e^x$, llegamos a la ecuación

$e^{2x}+6=5e^x$.

Reescribir esta ecuación como

$e^{2x}−5e^x+6=0$,

entonces podemos reescribirlo como una ecuación cuadrática en$e^x$:

$(e^x)^2−5(e^x)+6=0.$

Ahora podemos resolver la ecuación cuadrática. Factorizando esta ecuación, obtenemos

$(e^x−3)(e^x−2)=0.$

Por lo tanto, las soluciones satisfacen$e^x=3$ y$e^x=2$. Tomar el logaritmo natural de ambos lados nos da las soluciones$x=\ln 3,\ln 2$.

Ejercicio$\PageIndex{4}$

Resolver

$$e^{2x}/(3+e^{2x})=1/2. \nonumber$$

Pista

Primero resuelve la ecuación para$e^{2x}$

Contestar

$x=\dfrac{\ln 3}{2}$.

Ejemplo$\PageIndex{5}$: Solving Equations Involving Logarithmic Functions

Resuelve cada una de las siguientes ecuaciones para$x$.

1. $\ln \left(\dfrac{1}{x}\right)=4$
2. $\log_{10}\sqrt{x}+\log_{10}x=2$
3. $\ln (2x)−3\ln (x^2)=0$

Solución

a. Por la definición de la función de logaritmo natural,

$\ln \left(\dfrac{1}{x} \right)=4$

• si y sólo si$e^4=\dfrac{1}{x}$.

Por lo tanto, la solución es$x=1/e^4$.

b. Usando las propiedades product (Equation\ ref {productprop}) y power (Equation\ ref {powerprop}) de las funciones logarítmicas, reescriba el lado izquierdo de la ecuación como

$$\begin{align*} \log_{10}\sqrt{x} + \log_{10}x &= \log_{10} x \sqrt{x} \\[4pt] &= \log_{10}x^{3/2} \\[4pt] &= \dfrac{3}{2}\log_{10}x. \end{align*}$$

Por lo tanto, la ecuación se puede reescribir como

$\dfrac{3}{2}\log_{10}x=2$

o

$\log_{10}x=\dfrac{4}{3}$.

La solución es$x=10^{4/3}=10\sqrt[3]{10}$.

c. Usando la propiedad power (Ecuación\ ref {powerprop}) de las funciones logarítmicas, podemos reescribir la ecuación como$\ln (2x)−\ln (x^6)=0$.

Usando la propiedad cociente (Ecuación\ ref {quotientprop}), esto se convierte en

$\ln \left(\dfrac{2}{x^5}\right)=0$

Por lo tanto$2/x^5=1$,, lo que implica$x=\sqrt[5]{2}$. Entonces debemos verificar si hay alguna solución extraña.

Ejercicio$\PageIndex{5}$

Resolver$\ln (x^3)−4\ln (x)=1$.

Pista

Primero use la propiedad power, luego use la propiedad product de logaritmos.

Contestar

$x=\dfrac{1}{e}$

Al evaluar una función logarítmica con una calculadora, es posible que haya notado que las únicas opciones son$\log_{10}$ o$\log$, llamado logaritmo común, o$\ln$, que es el logaritmo natural. Sin embargo, las funciones exponenciales y las funciones de logaritmo se pueden expresar en términos de cualquier base deseada$b$. Si necesita usar una calculadora para evaluar una expresión con una base diferente, primero puede aplicar las fórmulas de cambio de base. Usando este cambio de base, normalmente escribimos una función exponencial o logarítmica dada en términos de las funciones exponenciales naturales y logarítmicas naturales.

Regla: Fórmulas de cambio de base

Vamos$a>0,\,b>0$, y$a≠1,\,b≠1$.

1. $a^x=b^{x \log_ba}$para cualquier número real$x$.

Si$b=e$, esta ecuación se reduce a$a^x=e^{x \log_ea}=e^{x \ln a}$.

2. $\log_ax=\dfrac{\log_bx}{\log_ba}$para cualquier número real$x>0$.

Si$b=e$, esta ecuación se reduce a$\log_ax=\dfrac{\ln x}{\ln a}$.

Prueba

Para la primera fórmula de cambio de base, comenzamos haciendo uso de la propiedad power de las funciones logarítmicas. Sabemos que para cualquier base$b>0,\, b≠1$,$\log_b(a^x)=x \log_ba$. Por lo tanto,

$b^{\log_b(a^x)}$=$b^{x \log_ba}$.

Además, lo sabemos$b^x$ y$\log_b(x)$ son funciones inversas. Por lo tanto,

$b^{\log_b(a^x)}=a^x$.

Combinando estas dos últimas igualdades, concluimos que$a^x=b^{x \log_ba}$.

Para probar el segundo inmueble, demostramos que

$(\log_ba)⋅(\log_ax)=\log_bx.$

Vamos$u=\log_ba,v=\log_ax$, y$w=\log_bx$. Eso lo demostraremos$u⋅v=w$. Por la definición de funciones logarítmicas, lo sabemos$b^u=a,\, a^v=x$, y$b^w=x$. De las ecuaciones anteriores, vemos que

$b^{uv}=(b^u)^v=a^v=x=b^w.$

Por lo tanto,$b^{uv}=b^w$. Dado que las funciones exponenciales son uno a uno, podemos concluir que$u⋅v=w$.

$\square$

Ejemplo$\PageIndex{6}$: Changing Bases

Utilice una utilidad de cálculo para evaluar$\log_37$ con la fórmula de cambio de base presentada anteriormente.

Solución

Utilice la segunda ecuación con$a=3$ y$b=e$:$\log_37=\dfrac{\ln 7}{\ln 3}≈1.77124$.

Ejercicio$\PageIndex{6}$

Utilice la fórmula de cambio de base y una utilidad de cálculo para evaluar$\log_46$.

Pista

Utilice el cambio de base para reescribir esta expresión en términos de expresiones que involucran la función de logaritmo natural.

Contestar

$\log_46 = \dfrac{\ln 6}{\ln 4} \approx 1.29248$

Ejemplo$\PageIndex{7}$: The Richter Scale for Earthquakes

En 1935, Charles Richter desarrolló una escala (ahora conocida como la escala de Richter) para medir la magnitud de un terremoto. La escala es una escala logarítmica de base 10, y puede describirse de la siguiente manera: Considere un sismo con magnitud$R_1$ en la escala de Richter y un segundo terremoto con magnitud$R_2$ en la escala de Richter. Supongamos$R_1>R_2$, lo que significa que el sismo de magnitud$R_1$ es más fuerte, pero ¿cuánto más fuerte es que el otro sismo?

Figura$\PageIndex{6}$: (crédito: modificación de obra de Robb Hannawacker, NPS)

Una manera de medir la intensidad de un sismo es mediante el uso de un sismógrafo para medir la amplitud de las olas sísmicas. Si$A_1$ es la amplitud medida para el primer sismo y$A_2$ es la amplitud medida para el segundo sismo, entonces las amplitudes y magnitudes de los dos sismos satisfacen la siguiente ecuación:

$R_1−R_2=\log_{10}\left(\dfrac{A1}{A2}\right)$.

Considera un sismo que mide 8 en la escala de Richter y un sismo que mide 7 en la escala de Richter. Entonces,

$8−7=\log_{10}\left(\dfrac{A1}{A2}\right)$.

Por lo tanto,

$\log_{10}\left(\dfrac{A1}{A2}\right)=1$,

lo que implica$A_1/A_2=10$ o$A_1=10A_2$. Ya que$A_1$ es 10 veces el tamaño de$A_2$, decimos que el primer sismo es 10 veces más intenso que el segundo sismo. Por otro lado, si un sismo mide 8 en la escala de Richter y otro mide 6, entonces la intensidad relativa de los dos sismos satisface la ecuación

$\log_{10}\left(\dfrac{A1}{A2}\right)=8−6=2$.

Por lo tanto,$A_1=100A_2$ .Es decir, el primer sismo es 100 veces más intenso que el segundo sismo.

¿Cómo podemos usar funciones logarítmicas para comparar la gravedad relativa del terremoto de magnitud 9 en Japón en 2011 con el terremoto de magnitud 7.3 en Haití en 2010?

Solución

Para comparar los sismos de Japón y Haití, podemos usar una ecuación presentada anteriormente:

$9−7.3=\log_{10}\left(\dfrac{A1}{A2}\right)$.

Por lo tanto$A_1/A_2=10^{1.7}$,, y concluimos que el sismo en Japón fue aproximadamente 50 veces más intenso que el sismo en Haití.

Ejercicio$\PageIndex{7}$

Comparar la gravedad relativa de un$8.4$ sismo de magnitud con un$7.4$ sismo de magnitud.

Pista

$R_1−R_2=\log_{10}(A1/A2)$.

Contestar

El$8.4$ sismo de magnitud es aproximadamente$10$ veces más o menos tan severo como el$7.4$ terremoto de magnitud.

Funciones hiperbólicas

Las funciones hiperbólicas se definen en términos de ciertas combinaciones de$e^x$ y$e^{−x}$. Estas funciones surgen naturalmente en diversas aplicaciones de ingeniería y física, incluyendo el estudio de las ondas de agua y las vibraciones de las membranas elásticas. Otro uso común para una función hiperbólica es la representación de una cadena o cable colgante, también conocida como catenaria (Figura$\PageIndex{7}$). Si introducimos un sistema de coordenadas para que el punto bajo de la cadena se encuentre a lo largo$y$ del eje, podemos describir la altura de la cadena en términos de una función hiperbólica. Primero, definimos las funciones hiperbólicas.

Figura:La$\PageIndex{7}$ forma de un hilo de seda en una tela de araña se puede describir en términos de una función hiperbólica. La misma forma se aplica a una cadena o cable que cuelga de dos soportes con solo su propio peso. (crédito: “Mtpaley”, Wikimedia Commons)

Definiciones: funciones hiperbólicas

Coseno hiperbólico

$\cosh x=\dfrac{e^x+e^{−x}}{2}$

Seno hiperbólico

$\sinh x=\dfrac{e^x−e^{−x}}{2}$

Tangente hiperbólica

$\tanh x=\dfrac{\sinh x}{\cosh x}=\dfrac{e^x−e^{−x}}{e^x+e^{−x}}$

Cosecante hiperbólico

$\operatorname{csch}x=\dfrac{1}{\sinh x}=\dfrac{2}{e^x−e^{−x}}$

Secante hiperbólica

$\operatorname{sech}x=\dfrac{1}{\cosh x}=\dfrac{2}{e^x+e^{−x}}$

Cotangente hiperbólica

$\coth x=\dfrac{\cosh x}{\sinh x}=\dfrac{e^x+e^{−x}}{e^x−e^{−x}}$

El nombre$\cosh$ rima con “dios”, mientras que el nombre$\sinh$ se pronuncia “cincha”. $\operatorname{Tanh}, \,\operatorname{sech}, \, \operatorname{csch},$y$\coth$ se pronuncian “tanch”, “seech”, “coseech” y “cotanch”, respectivamente.

Utilizando la definición$\cosh(x)$ y principios de la física, se puede demostrar que la altura de una cadena colgante, como la de la Figura$\PageIndex{8}$, puede ser descrita por la función$h(x)=a\cosh(x/a) + c$ para ciertas constantes$a$ y$c$.

Pero, ¿por qué estas funciones se llaman funciones hiperbólicas? Para responder a esta pregunta, considere la cantidad$\cosh^2 t − \sinh^2 t$. Usando la definición de$\cosh$ y$\sinh$, vemos que

$$\cosh^2 t − \sinh^2 t=\dfrac{e^{2t}+2+e^{−2t}}{4}−\dfrac{e^{2t}−2+e^{−2t}}{4}=1. \nonumber$$

Esta identidad es el análogo de la identidad trigonométrica$\cos^2 t + \sin^2 t=1$. Aquí, dado un valor$t$, el punto$(x,y)=(\cosh t,\,\sinh t)$ se encuentra en la hipérbola unitaria$x^2−y^2=1$ (Figura$\PageIndex{8}$).

Figura$\PageIndex{8}$: La hipérbola unitaria$\cosh^2 t − \sinh^2 t=1$.

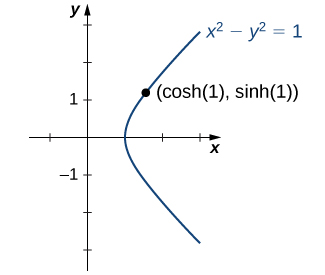
Gráficas de Funciones Hiperbólicas

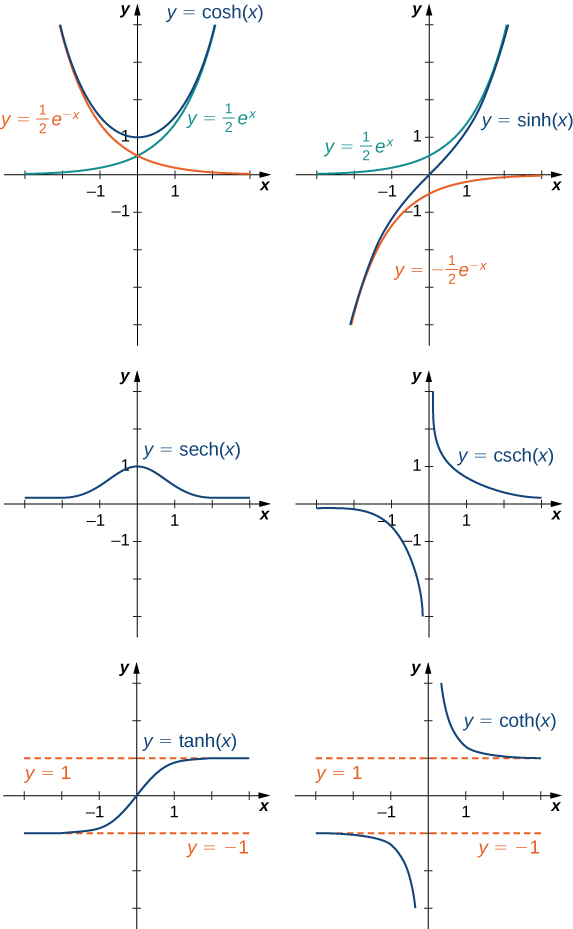
Para graficar$\cosh x$ y$\sinh x$, hacemos uso del hecho de que ambas funciones se acercan$(1/2)e^x$ como$x→∞$, ya que$e^{−x}→0$ como$x→∞$. Como$x→−∞,\cosh x$ enfoques$1/2e^{−x}$, mientras que$\sinh x$ enfoques$−1/2e^{−x}$. Por lo tanto, utilizando las gráficas de$1/2e^x,1/2e^{−x}$, y$−1/2e^{−x}$ como guías, graficamos$\cosh x$ y$\sinh x$. Para graficar$\tanh x$, utilizamos el hecho de que$\tanh(0)=0$,$−1<\tanh(x)<1$ para todos$x$,$\tanh x→1$ como$x→∞$, y$\tanh x→−1$ como$x→−∞$. Las gráficas de las otras tres funciones hiperbólicas se pueden esbozar utilizando las gráficas de$\cosh x$$\sinh x$, y$\tanh x$ (Figura$\PageIndex{9}$).

Figura$\PageIndex{9}$: Las funciones hiperbólicas implican combinaciones de$e^x$ y$e^{−x}$.

Identidades que involucran funciones hiperbólicas

La identidad$\cosh^2 t−\sinh^2 t = 1$, mostrada en la Figura$\PageIndex{8}$, es una de varias identidades que involucran las funciones hiperbólicas, algunas de las cuales se enumeran a continuación. Las primeras cuatro propiedades se derivan fácilmente de las definiciones de seno hiperbólico y coseno hiperbólico. Excepto por algunas diferencias en los signos, la mayoría de estas propiedades son análogas a las identidades para funciones trigonométricas.

Identidades que involucran funciones hiperbólicas

1. $\cosh(−x)=\cosh x$
2. $\sinh(−x)=−\sinh x$
3. $\cosh x+\sinh x=e^x$
4. $\cosh x−\sinh x=e^{−x}$
5. $\cosh^2 x−\sinh^2 x=1$
6. $1−\tanh^2 x=\operatorname{sech}^2 x$
7. $\coth^2 x −1=\operatorname{csch}^2 x$
8. $\sinh(x±y)=\sinh x \cosh y ± \cosh x \sinh y$
9. $\cosh(x±y)=\cosh x \cosh y ± \sinh x \sinh y$

Ejemplo$\PageIndex{8}$: Evaluating Hyperbolic Functions

1. Simplificar$\sinh(5\ln x)$.
2. Si$\sinh x=3/4$, encuentra los valores de las cinco funciones hiperbólicas restantes.

Solución:

a. Usando la definición de la$\sinh$ función, escribimos

$\sinh(5\ln x)=\dfrac{e^{5\ln x}−e^{−5\ln x}}{2}=\dfrac{e^{\ln (x^5)}−e^{\ln (x^{−5})}}{2}=\dfrac{x^5−x^{−5}}{2}.$

b. Utilizando la identidad$\cosh^2 x − \sinh^2 x=1$, vemos que

$\cosh^2 x=1+\left(\frac{3}{4}\right)^2=\dfrac{25}{16}.$

Ya que$\cosh x≥1$ para todos$x$, debemos tener$\cosh x=5/4$. Luego, usando las definiciones para las otras funciones hiperbólicas, concluimos que$\tanh x=3/5,\operatorname{csch}x=4/3,\operatorname{sech}x=4/5$, y$\coth x=5/3$.

Ejercicio$\PageIndex{8}$

Simplificar$\cosh(2\ln x)$.

Pista

Utilice la definición de la$\cosh$ función y la propiedad power de las funciones logaritmo.

Contestar

$(x^2+x^{−2})/2$

Funciones hiperbólicas inversas

A partir de las gráficas de las funciones hiperbólicas, vemos que todas ellas son uno-a-uno excepto$\cosh x$ y$\operatorname{sech}x$. Si restringimos los dominios de estas dos funciones al intervalo$[0,∞),$ entonces todas las funciones hiperbólicas son uno a uno, y podemos definir las funciones hiperbólicas inversas. Dado que las funciones hiperbólicas en sí mismas involucran funciones exponenciales, las funciones hiperbólicas inversas involucran funciones logarítmicas.

Definiciones: Funciones hiperbólicas inversas

\ [\ begin {align*} &\ sinh^ {−1} x =\ nombreoperador {arcsinh} x=\ ln\ izquierda (x+\ sqrt {x^2+1}\ derecha) &\ cosh^ {−1} x =\ nombreoperador {arccosh} x=\ ln\ izquierda (x+\ sqrt {x^2−1}\ derecha)\ [4pt]
&\ tanh^ {−1} x=\ nombreoperador {arctanh} x=\ dfrac {1} {2}\ ln\ izquierda (\ dfrac {1+x} {1−x}\ derecha) &\ coth^ {−1} x =\ nombreoperador {arccot} x=\ frac {1} {2}\ ln\ izquierda (\ dfrac {x+1} {x−1}\ derecha)\\ [4pt]
&\ nombreoperador {sech} ^ {−1} x=\ nombreoperador {arcsech} x=\ ln\ izquierda (\ dfrac {1+\ sqrt {1−x^2} {x}\ derecha) &\ nombreoperador {csch} ^ {−1} x=\ nombreoperador {arccsch} x=\ ln\ izquierda (\ dfrac {1} {x} +\ dfrac {\ sqrt {1+x^2}} {|x|}\ derecha)\ end { alinear*}\]

Veamos cómo derivar la primera ecuación. Los demás siguen de manera similar. Supongamos$y=\sinh^{−1}x$. Entonces,$x=\sinh y$ y, por la definición de la función sinusoidal hiperbólica,$x=\dfrac{e^y−e^{−y}}{2}$. Por lo tanto,

$e^y−2x−e^{−y}=0.$

Multiplicando esta ecuación por$e^y$, obtenemos

$e^{2y}−2xe^y−1=0$.

Esto se puede resolver como una ecuación cuadrática, con la solución

$e^y=\dfrac{2x±\sqrt{4x^2+4}}{2}=x±\sqrt{x^2+1}$.

Ya que$e^y>0$, la única solución es la que tiene el signo positivo. Aplicando el logaritmo natural a ambos lados de la ecuación, concluimos que

$y=\ln (x+\sqrt{x^2+1}).$

Ejemplo$\PageIndex{9}$: Evaluating Inverse Hyperbolic Functions

Evalúe cada una de las siguientes expresiones.

$\sinh^{−1}(2)$

$\tanh^{−1}(1/4)$

Solución:

$$\sinh^{−1}(2)=\ln (2+\sqrt{2^2+1})=\ln (2+\sqrt{5})≈1.4436\nonumber$$

$$\tanh^{−1}(1/4)=\frac{1}{2}\ln \left(\dfrac{1+1/4}{1−1/4}\right)=\frac{1}{2}\ln \left(\dfrac{5/4}{3/4}\right)=\frac{1}{2}\ln \left(\dfrac{5}{3}\right)≈0.2554\nonumber$$

Ejercicio$\PageIndex{9}$

Evaluar$\tanh^{−1}(1/2)$.

Pista

Utilice la definición de$\tanh^{−1}x$ y simplifique.

Contestar

$\dfrac{1}{2}\ln (3)≈0.5493$.

Conceptos clave

• La función exponencial$y=b^x$ está aumentando si$b>1$ y disminuyendo si$0<b<1$. Su dominio es$(−∞,∞)$ y su rango es$(0,∞)$.
• La función logarítmica$y=\log_b(x)$ es la inversa de$y=b^x$. Su dominio es$(0,∞)$ y su rango es$(−∞,∞).$
• La función exponencial natural es$y=e^x$ y la función logarítmica natural es$y=\ln x=\log_ex.$
• Dada una función exponencial o función logarítmica en base$a$, podemos hacer un cambio de base para convertir esta función a cualquier base$b>0$, normalmente$b≠1.$ convertimos a base$e$.
• Las funciones hiperbólicas implican combinaciones de las funciones exponenciales$e^x$ y$e^{−x}.$ como resultado, las funciones hiperbólicas inversas involucran el logaritmo natural.

Glosario

base

el número$b$ en la función exponencial$f(x)=b^x$ y la función logarítmica$f(x)=\log_bx$

exponente

el valor$x$ en la expresión$b^x$

funciones hiperbólicas

las funciones denotadas$\sinh,\,\cosh,\,\operatorname{tanh},\,\operatorname{csch},\,\operatorname{sech},$ y$\coth$, que implican ciertas combinaciones de$e^x$ y$e^{−x}$

funciones hiperbólicas inversas

las inversas de las funciones hiperbólicas donde$\cosh$ y$\operatorname{sech}$ están restringidas al dominio$[0,∞)$; cada una de estas funciones se puede expresar en términos de una composición de la función logaritmo natural y una función algebraica

función exponencial natural

la función$f(x)=e^x$

logaritmo natural

la función$\ln x=\log_ex$

número e

a medida que$m$ aumenta, la cantidad$(1+(1/m)^m$ se acerca a algún número real; definimos ese número real para que sea$e;$ el valor de$e$ es aproximadamente$2.718282$