6.1: Áreas entre curvas

Última actualización
Guardar como PDF

Page ID: 116191

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Objetivos de aprendizaje

Determinar el área de una región entre dos curvas integrando con respecto a la variable independiente.
Encuentra el área de una región compuesta.
Determinar el área de una región entre dos curvas integrando con respecto a la variable dependiente.

En Introducción a la Integración, desarrollamos el concepto de la integral definida para calcular el área por debajo de una curva en un intervalo dado. En esta sección, ampliamos esa idea para calcular el área de regiones más complejas. Comenzamos por encontrar el área entre dos curvas que son funciones de$\displaystyle x$, comenzando por el simple caso en el que un valor de función es siempre mayor que el otro. Luego miramos casos en los que las gráficas de las funciones se cruzan. Por último, consideramos cómo calcular el área entre dos curvas que son funciones de$\displaystyle y$.

Área de una región entre dos curvas

Dejar$\displaystyle f(x)$ y$\displaystyle g(x)$ ser funciones continuas a lo largo de un intervalo$\displaystyle [a,b]$ tal que$\displaystyle f(x)≥g(x)$ encendido$\displaystyle [a,b]$. Queremos encontrar el área entre las gráficas de las funciones, como se muestra en la Figura$\PageIndex{1}$.

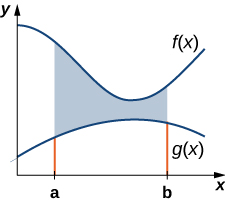
Esta figura es una gráfica en el primer cuadrante. Hay dos curvas en la gráfica. La curva superior está etiquetada como “f (x)” y la curva inferior está etiquetada como “g (x)”. Hay dos límites en el eje x etiquetados a y b. Hay un área sombreada entre las dos curvas delimitadas por líneas en x=a y x=b. — Figura$\PageIndex{1}$: El área entre las gráficas de dos funciones,$\displaystyle f(x)$ y$\displaystyle g(x)$, en el intervalo$\displaystyle [a,b]$

Como hicimos antes, vamos a particionar el intervalo en el eje x y aproximar el área entre las gráficas de las funciones con rectángulos. Entonces, para$\displaystyle i=0,1,2,…,n$, deja$\displaystyle P={x_i}$ ser una partición regular de$\displaystyle [a,b]$. Luego, para$\displaystyle i=1,2,…,n,$ elegir un punto$\displaystyle x^∗_i∈[x_{i−1},x_i]$, y en cada intervalo$\displaystyle [x_{i−1},x_i]$ construir un rectángulo que se extiende verticalmente de$\displaystyle g(x^∗_i)$ a$\displaystyle f(x^∗_i)$. La figura$\PageIndex{2a}$ muestra los rectángulos cuando$\displaystyle x^∗_i$ se selecciona para ser el punto final izquierdo del intervalo y$\displaystyle n=10$. La figura$\PageIndex{2b}$ muestra un rectángulo representativo en detalle.

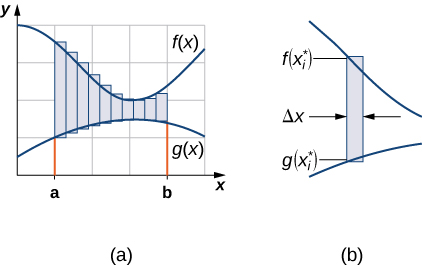
Esta figura tiene tres gráficas. La primera gráfica tiene dos curvas, una sobre la otra. Entre las curvas hay un rectángulo. La parte superior del rectángulo está en la curva superior etiquetada como “f (x*)” y la parte inferior del rectángulo está en la curva inferior y etiquetada como “g (x*)”. La segunda gráfica, etiquetada como “(a)”, tiene dos curvas en la gráfica. La curva superior está etiquetada como “f (x)” y la curva inferior está etiquetada como “g (x)”. Hay dos límites en el eje x etiquetados a y b. Hay un área sombreada entre las dos curvas delimitadas por líneas en x=a y x=b. La tercera gráfica, etiquetada como “(b)” tiene dos curvas una sobre la otra. La primera curva está etiquetada como “f (x*)” y la curva inferior está etiquetada como “g (x*)”. Hay un rectángulo sombreado entre los dos. El ancho del rectángulo se etiqueta como “delta x”. — Figura$\PageIndex{2}$: (a) Podemos aproximar el área entre las gráficas de dos funciones,$\displaystyle f(x)$ y$\displaystyle g(x)$, con rectángulos. b) El área de un rectángulo típico va de una curva a otra.

La altura de cada rectángulo individual es$\displaystyle f(x^∗_i)−g(x^∗_i)$ y el ancho de cada rectángulo es$\displaystyle Δx$. Sumando las áreas de todos los rectángulos, vemos que el área entre las curvas se aproxima por

\[\displaystyle A≈\sum_{i=1}^n[f(x^∗_i)−g(x^∗_i)]Δx. \nonumber \]

Esta es una suma de Riemann, así que tomamos el límite como$\displaystyle n→∞$ y obtenemos

\[\displaystyle A=\lim_{n→∞}\sum_{i=1}^n[f(x^∗_i)−g(x^∗_i)]Δx=\int ^b_a[f(x)−g(x)]dx. \nonumber \]

Estos hallazgos se resumen en el siguiente teorema.

Encontrar el área entre dos curvas

Dejar$\displaystyle f(x)$ y$\displaystyle g(x)$ ser funciones continuas de tal manera que$\displaystyle f(x)≥g(x)$ a lo largo de un intervalo [$\displaystyle a,b]$. Que R denote la región delimitada arriba por la gráfica de$\displaystyle f(x)$, abajo por la gráfica de$\displaystyle g(x)$, y a la izquierda y derecha por las líneas$\displaystyle x=a$ y$\displaystyle x=b$, respectivamente. Entonces, el área de$\textbf{R}$ es dada por

\[A=\int ^b_a[f(x)−g(x)]dx. \nonumber \]

Aplicamos este teorema en el siguiente ejemplo.

Ejemplo$\PageIndex{1}$: Finding the Area of a Region between Two Curves I

Si$\textbf{R}$ es la región delimitada arriba por la gráfica de la función$\displaystyle f(x)=x+4$ y abajo por la gráfica de la función$\displaystyle g(x)=3−\dfrac{x}{2}$ sobre el intervalo$\displaystyle [1,4]$, busque el área de región$\textbf{R}$.

Solución

La región se representa en la siguiente figura.

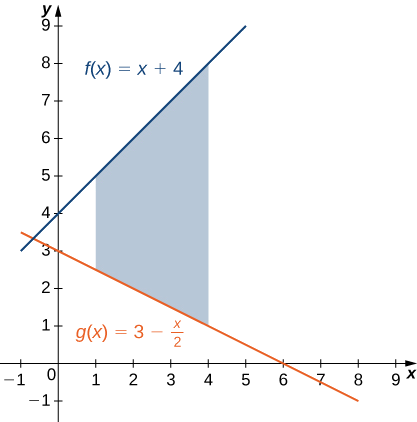
Esta figura tiene dos gráficas lineales en el primer cuadrante. Son las funciones f (x) = x+4 y g (x) = 3-x/2. Entre estas líneas se encuentra una región sombreada, delimitada arriba por f (x) y abajo por g (x). El área sombreada está entre x=1 y x=4. — Figura$\PageIndex{3}$: Se muestra una región entre dos curvas donde una curva es siempre mayor que la otra.

Tenemos

\[ \begin{align*} A =\int ^b_a[f(x)−g(x)]\,dx \\[4pt] =\int ^4_1[(x+4)−(3−\dfrac{x}{2})]\,dx=\int ^4_1\left[\dfrac{3x}{2}+1\right]\,dx \\[4pt] =[\dfrac{3x^2}{4}+x]\bigg|^4_1=(16−\dfrac{7}{4})=\dfrac{57}{4}. \end{align*}\]

El área de la región es$\displaystyle \dfrac{57}{4}units^2$.

Ejercicio$\PageIndex{1}$

Si$\textbf{R}$ es la región delimitada por las gráficas de las funciones$\displaystyle f(x)=\dfrac{x}{2}+5$ y$\displaystyle g(x)=x+\dfrac{1}{2}$ sobre el intervalo$\displaystyle [1,5]$, busque el área de región$\textbf{R}$.

Insinuación: Grafique las funciones para determinar qué gráfico de función forma el límite superior y cuál forma el límite inferior, luego siga el proceso utilizado en Ejemplo.

Contestar: $\displaystyle 12$unidades ²

En Ejemplo$\PageIndex{1}$, definimos el intervalo de interés como parte de la declaración del problema. Muy a menudo, sin embargo, queremos definir nuestro intervalo de interés en función de dónde se cruzan las gráficas de las dos funciones. Esto se ilustra en el siguiente ejemplo.

Ejemplo$\PageIndex{2}$: Finding the Area of a Region between Two Curves II

Si$\textbf{R}$ es la región delimitada arriba por la gráfica de la función$\displaystyle f(x)=9−(x/2)^2$ y abajo por la gráfica de la función$\displaystyle g(x)=6−x$, busque el área de región$\textbf{R}$.

Solución

La región se representa en la siguiente figura.

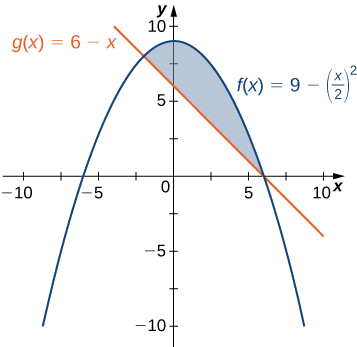
Esta figura tiene dos gráficas en el primer cuadrante. Son las funciones f (x) = 9- (x/2) ^2 y g (x) = 6-x. Entre estas gráficas, una parábola invertida y una línea, es una región sombreada, delimitada arriba por f (x) y abajo por g (x). — Figura$\PageIndex{4}$: Esta gráfica muestra la región debajo de la gráfica$\displaystyle f(x)$ y por encima de la gráfica de$\displaystyle g(x).$

Primero necesitamos calcular dónde se cruzan las gráficas de las funciones. Configuración$\displaystyle f(x)=g(x),$ que obtenemos

\[ \begin{align*} \displaystyle f(x) =g(x) \\[4pt] 9−(\dfrac{x}{2})^2 =6−x\\[4pt] 9−\dfrac{x^2}{4} =6−x\\[4pt] 36−x^2 =24−4x\\[4pt] x^2−4x−12 =0\\[4pt] (x−6)(x+2) =0. \end{align*}\]

Las gráficas de las funciones se cruzan cuando más$\displaystyle x=6$ o$\displaystyle x=−2,$ menos queremos integrar de$\displaystyle −2$ a$\displaystyle 6$. Ya que$\displaystyle f(x)≥g(x)$ para$\displaystyle −2≤x≤6,$ obtenemos

\[\begin{align*} \displaystyle A =\int ^b_a[f(x)−g(x)]\,dx \\ =\int ^6_{−2} \left[9−(\dfrac{x}{2})^2−(6−x)\right]\,dx \\ =\int ^6_{−2}\left[3−\dfrac{x^2}{4}+x\right]\,dx \\ = \left. \left[3x−\dfrac{x^3}{12}+\dfrac{x^2}{2}\right] \right|^6_{−2}=\dfrac{64}{3}. \end{align*}\]

El área de la región es de$\displaystyle 64/3$ unidades ².

Ejercicio$\PageIndex{2}$

Si$\textbf{R}$ es la región delimitada arriba por la gráfica de la función$\displaystyle f(x)=x$ y abajo por la gráfica de la función$\displaystyle g(x)=x^4$, busque el área de región$\textbf{R}$.

Insinuación: Utilice el proceso de Ejemplo$\PageIndex{2}$.

Contestar: $\displaystyle \dfrac{3}{10}$unidad ²

Áreas de Regiones Comidas

Hasta el momento, hemos requerido$\displaystyle f(x)≥g(x)$ a lo largo de todo el intervalo de interés, pero ¿y si queremos mirar regiones delimitadas por las gráficas de funciones que se cruzan entre sí? En ese caso, modificamos el proceso que acabamos de desarrollar utilizando la función de valor absoluto.

Encontrar el área de una región entre curvas que se cruzan

Dejar$\displaystyle f(x)$ y$\displaystyle g(x)$ ser funciones continuas a lo largo de un intervalo$\displaystyle [a,b]$. Dejar$\textbf{R}$ denotar la región entre las gráficas de$\displaystyle f(x)$ y$\displaystyle g(x)$, y estar delimitada a la izquierda y a la derecha por las líneas$\displaystyle x=a$ y$\displaystyle x=b$, respectivamente. Entonces, el área de$\textbf{R}$ es dada por

\[A=\int ^b_a|f(x)−g(x)|dx. \nonumber \]

En la práctica, aplicar este teorema nos obliga a romper el intervalo$\displaystyle [a,b]$ y evaluar varias integrales, dependiendo de cuál de los valores de la función sea mayor en una parte dada del intervalo. Estudiamos este proceso en el siguiente ejemplo.

Ejemplo$\PageIndex{3}$: Finding the Area of a Region Bounded by Functions That Cross

Si$\textbf{R}$ es la región entre las gráficas de las funciones$\displaystyle f(x)=\sin x $ y$\displaystyle g(x)=\cos x$ sobre el intervalo$\displaystyle [0,π]$, busque el área de región$\textbf{R}$.

Solución

La región se representa en la siguiente figura.

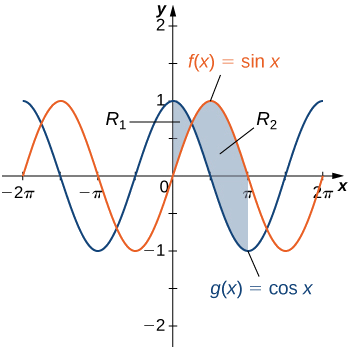
Esta figura tiene dos gráficas. Son las funciones f (x) = sinx y g (x) = cosx. Ambas son funciones periódicas que se asemejan a las ondas. Hay dos áreas sombreadas entre las gráficas. La primera área sombreada está etiquetada con “R1” y tiene g (x) por encima de f (x). Esta región comienza en el eje y y se detiene donde se cruzan las curvas. La segunda región está etiquetada como “R2” y comienza en la intersección con f (x) por encima de g (x). La región sombreada se detiene en x=pi. — Figura$\PageIndex{5}$: La región entre dos curvas se puede dividir en dos subregiones.

Las gráficas de las funciones se cruzan en$\displaystyle x=π/4$. Por$\displaystyle x∈[0,π/4], \cos x≥\sin x ,$ lo

$\displaystyle |f(x)−g(x)|=|\sin x −\cos x|=\cos x−\sin x .$

Por otro lado, para$\displaystyle x∈[π/4,π], \sin x ≥\cos x,$ así

$\displaystyle |f(x)−g(x)|=|\sin x −\cos x|=\sin x −\cos x.$

Entonces

\[ \begin{align*} A =\int ^b_a|f(x)−g(x)|dx \\[4pt] =\int ^π_0|\sin x −\cos x|dx=\int ^{π/4}_0(\cos x−\sin x )dx+\int ^{π}_{π/4}(\sin x −\cos x)dx \\[4pt] =[\sin x +\cos x]|^{π/4}_0+[−\cos x−\sin x ]|^π_{π/4} \\[4pt] =(\sqrt{2}−1)+(1+\sqrt{2})=2\sqrt{2}. \end{align*}\]

El área de la región es de$\displaystyle 2\sqrt{2}$ unidades ^₂.

Ejercicio$\PageIndex{3}$

Si$\textbf{R}$ es la región entre las gráficas de las funciones$\displaystyle f(x)=\sin x $ y$\displaystyle g(x)=\cos x$ sobre el intervalo$\displaystyle [π/2,2π]$, busque el área de región$\textbf{R}$.

Insinuación: Las dos curvas se cruzan en$\displaystyle x=(5π)/4.$

Contestar: $\displaystyle 2+2\sqrt{2}$unidades ²

Ejemplo$\PageIndex{4}$: Finding the Area of a Complex Region

Consideremos la región representada en la Figura$\PageIndex{6}$. Encuentra el área de$\textbf{R}$.

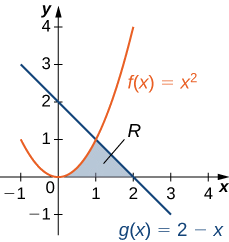
Esta figura tiene dos gráficas en el primer cuadrante. Son las funciones f (x) = x^2 y g (x) = 2-x. Entre estas gráficas se encuentra una región sombreada, delimitada a la izquierda por f (x) y a la derecha por g (x). Todo lo cual está por encima del eje x. La región está etiquetada como R. El área sombreada está entre x=0 y x=2. — Figura$\PageIndex{6}$: Se requieren dos integrales para calcular el área de esta región.

Solución

Al igual que con Ejemplo$\PageIndex{3}$, necesitamos dividir el intervalo en dos piezas. Las gráficas de las funciones se cruzan en$\displaystyle x=1$ (set$\displaystyle f(x)=g(x)$ y solve para x), por lo que evaluamos dos integrales separadas: una sobre el intervalo$\displaystyle [0,1]$ y otra sobre el intervalo$\displaystyle [1,2]$.

A lo largo del intervalo$\displaystyle [0,1]$, la región está delimitada por arriba$\displaystyle f(x)=x^2$ y por debajo por el eje x, por lo que tenemos

$\displaystyle A_1=\int ^1_0x^2dx=\dfrac{x^3}{3}∣^1_0=\dfrac{1}{3}.$

A lo largo del intervalo$\displaystyle [1,2],$ la región está delimitada por arriba$\displaystyle g(x)=2−x$ y por debajo por el eje x, por lo que tenemos

$\displaystyle A_2=\int ^2_1(2−x)dx=[2x−\dfrac{x^2}{2}]∣^2_1=\dfrac{1}{2}.$

Sumando estas áreas, obtenemos

$\displaystyle A=A_1+A_2=\dfrac{1}{3}+\dfrac{1}{2}=\dfrac{5}{6}.$

El área de la región es de$\displaystyle 5/6$ unidades ²^.

Ejercicio$\PageIndex{4}$

Consideremos la región representada en la siguiente figura. Encuentra el área de$\textbf{R}$.

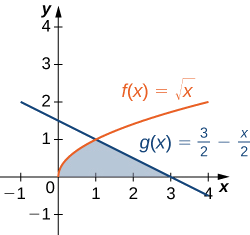
$Esta figura tiene dos gráficas en el primer cuadrante. Son las funciones f (x) = cuadratura de x y g (x) = 3/2 — x/2. Entre estas gráficas se encuentra una región sombreada, delimitada a la izquierda por f (x) y a la derecha por g (x). Todo lo cual está por encima del eje x. El área sombreada está entre x=0 y x=3.$

Insinuación: Las dos curvas se cruzan en x=1

Contestar: $\displaystyle \dfrac{5}{3}$unidades ²

Regiones definidas con respecto a y

En Ejemplo$\PageIndex{4}$, tuvimos que evaluar dos integrales separadas para calcular el área de la región. Sin embargo, hay otro enfoque que requiere sólo una integral. ¿Y si tratamos las curvas como funciones de$\displaystyle y$, en lugar de como funciones de$\displaystyle x$? Figura de revisión. Tenga en cuenta que la gráfica izquierda, mostrada en rojo, está representada por la función$\displaystyle y=f(x)=x^2$. Podríamos resolver esto con la misma facilidad para x y representar la curva por la función$\displaystyle x=v(y)=\sqrt{y}$. (Tenga en cuenta que también$\displaystyle x=−\sqrt{y}$ es una representación válida de$\displaystyle y=f(x)=x^2$ la función en función de$\displaystyle y$. No obstante, con base en la gráfica, es claro que estamos interesados en la raíz cuadrada positiva.) Del mismo modo, la gráfica derecha está representada por la función$\displaystyle y=g(x)=2−x$, pero con la misma facilidad podría ser representada por la función$\displaystyle x=u(y)=2−y$. Cuando las gráficas se representan como funciones de$\displaystyle y$, vemos que la región está delimitada a la izquierda por la gráfica de una función y a la derecha por la gráfica de la otra función. Por lo tanto, si nos integramos con respecto a$\displaystyle y$, necesitamos evaluar una integral solamente. Desarrollemos una fórmula para este tipo de integración.

Dejar$\displaystyle u(y)$ y$\displaystyle v(y)$ ser funciones continuas sobre un intervalo$\displaystyle [c,d]$ tal que$\displaystyle u(y)≥v(y)$ para todos$\displaystyle y∈[c,d]$. Queremos encontrar el área entre las gráficas de las funciones, como se muestra en la Figura$\PageIndex{7}$.

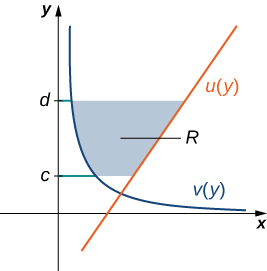
Esta figura tiene dos gráficas en el primer cuadrante. Son las funciones v (y) y u (y). Entre estas gráficas se encuentra una región sombreada, delimitada a la izquierda por v (y) y a la derecha por u (y). La región está etiquetada como R. El área sombreada se encuentra entre los límites horizontales de y=c e y=d. — Figura$\PageIndex{7}$: Podemos encontrar el área entre las gráficas de dos funciones,$\displaystyle u(y)$ y$\displaystyle v(y)$.

Esta vez, vamos a particionar el intervalo en el eje y y usar rectángulos horizontales para aproximar el área entre las funciones. Entonces, para$\displaystyle i=0,1,2,…,n$, deja$\displaystyle Q={y_i}$ ser una partición regular de$\displaystyle [c,d]$. Luego, para$\displaystyle i=1,2,…,n$, elija un punto$\displaystyle y^∗_i∈[y_{i−1},y_i]$, luego sobre cada intervalo$\displaystyle [y_{i−1},y_i]$ construya un rectángulo que se extienda horizontalmente de$\displaystyle v(y^0∗_i)$ a$\displaystyle u(y^∗_i)$. La figura$\PageIndex{8a}$ muestra los rectángulos cuando$\displaystyle y^∗_i$ se selecciona para ser el punto final inferior del intervalo y$\displaystyle n=10$. La figura$\PageIndex{8b}$ muestra un rectángulo representativo en detalle.

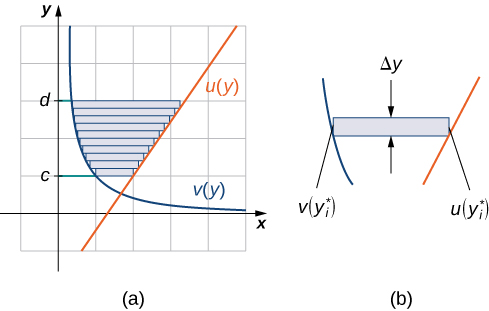
Esta cifra tiene tres gráficas. La primera figura tiene dos curvas. Son las funciones v (y*) y u (y*). Entre estas curvas se encuentra un rectángulo horizontal. La segunda figura etiquetada como “(a)”, es una región sombreada, delimitada a la izquierda por v (y) y a la derecha por u (y). El área sombreada se encuentra entre los límites horizontales de y=c e y=d, esta área sombreada se divide en rectángulos entre las curvas. La tercera figura, etiquetada como “(b)”, son las dos curvas v (y*) y u (y*). Entre las curvas hay un rectángulo horizontal con anchura delta y. — Figura$\PageIndex{8}$: (a) Aproximación del área entre las gráficas de dos funciones,$\displaystyle u(y)$ y$\displaystyle v(y)$, con rectángulos. b) El área de un rectángulo típico.

La altura de cada rectángulo individual es$\displaystyle Δy$ y el ancho de cada rectángulo es$\displaystyle u(y^∗_i)−v(y^∗_i)$. Por lo tanto, el área entre las curvas es aproximadamente

\[ A≈\sum_{i=1}^n[u(y^∗_i)−v(y^∗_i)]Δy . \nonumber \]

Esta es una suma de Riemann, así que tomamos el límite como$\displaystyle n→∞,$ obtener

\[ \begin{align*} A =\lim_{n→∞}\sum_{i=1}^n[u(y^∗_i)−v(y^∗_i)]Δy \\[4pt] =\int ^d_c[u(y)−v(y)]dy. \end{align*}\]

Estos hallazgos se resumen en el siguiente teorema.

Encontrar el área entre dos curvas, integrando a lo largo del eje y

Dejar$\displaystyle u(y)$ y$\displaystyle v(y)$ ser funciones continuas tales que$\displaystyle u(y)≥v(y) $ para todos$\displaystyle y∈[c,d]$. Dejar$\textbf{R}$ denotar la región delimitada a la derecha por la gráfica de$\displaystyle u(y)$, a la izquierda por la gráfica de$\displaystyle v(y)$, y arriba y abajo por las líneas$\displaystyle y=d$ y$\displaystyle y=c$, respectivamente. Entonces, el área de$\textbf{R}$ es dada por

\[A=\int ^d_c[u(y)−v(y)]dy. \nonumber \]

Ejemplo$\PageIndex{5}$: Integrating with Respect to y

Volvamos a visitar Ejemplo$\PageIndex{4}$, sólo que esta vez vamos a integrar con respecto a$\displaystyle y$. $\textbf{R}$Sea la región representada en la Figura$\PageIndex{9}$. Encuentra el área de$\textbf{R}$ integrando con respecto a$\displaystyle y$.

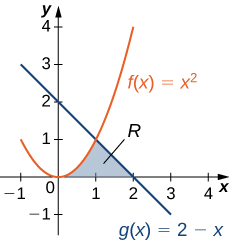
Solución

Primero debemos expresar las gráficas como funciones de$\displaystyle y$. Como vimos al principio de esta sección, la curva de la izquierda puede ser representada por la función$\displaystyle x=v(y)=\sqrt{y}$, y la curva de la derecha puede ser representada por la función$\displaystyle x=u(y)=2−y$.

Ahora tenemos que determinar los límites de la integración. La región está delimitada por debajo por el eje x, por lo que el límite inferior de integración es$\displaystyle y=0$. El límite superior de integración está determinado por el punto donde se cruzan las dos gráficas, que es el punto$\displaystyle (1,1)$, por lo que el límite superior de integración es$\displaystyle y=1$. Así, tenemos$\displaystyle [c,d]=[0,1]$.

Calculando el área de la región, obtenemos

\[ \begin{align*} A =\int ^d_c[u(y)−v(y)]dy \\[4pt] =\int ^1_0[(2−y)−\sqrt{y}]dy\\[4pt] =[2y−\dfrac{y^2}{2}−\dfrac{2}{3}y^{3/2}]∣^1_0\\[4pt] =\dfrac{5}{6}. \end{align*}\]

El área de la región es de$\displaystyle 5/6$ unidades ².

Ejercicio$\PageIndex{5}$

Volvamos a visitar el punto de control asociado con Ejemplo$\PageIndex{4}$, solo que esta vez, vamos a integrar con respecto a$\displaystyle y$. $\textbf{R}$Sea la región representada en la siguiente figura. Encuentra el área de$\textbf{R}$ integrando con respecto a$\displaystyle y$.

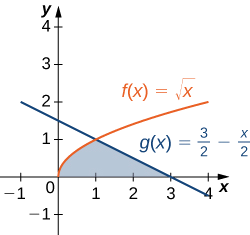
Insinuación: Sigue el proceso del ejemplo anterior.

Contestar: $\displaystyle \dfrac{5}{3}$unidades ²

Conceptos clave

Así como las integrales definidas se pueden usar para encontrar el área bajo una curva, también se pueden usar para encontrar el área entre dos curvas.
Para encontrar el área entre dos curvas definidas por funciones, integre la diferencia de las funciones.
Si las gráficas de las funciones se cruzan, o si la región es compleja, utilice el valor absoluto de la diferencia de las funciones. En este caso, puede ser necesario evaluar dos o más integrales y agregar los resultados para encontrar el área de la región.
A veces puede ser más fácil integrarse con respecto a y para encontrar el área. Los principios son los mismos independientemente de qué variable se utilice como variable de integración.

Ecuaciones Clave

Área entre dos curvas, integrándose en el eje x

$\displaystyle A=\int ^b_a[f(x)−g(x)]dx$

Área entre dos curvas, integrándose en el eje y

$\displaystyle A=\int ^d_c[u(y)−v(y)]dy$

Search

Text Color

Text Size

Margin Size

Font Type

Encontrar el área entre dos curvas

Ejemplo\(\PageIndex{1}\): Finding the Area of a Region between Two Curves I

Ejercicio\(\PageIndex{1}\)

Ejemplo\(\PageIndex{2}\): Finding the Area of a Region between Two Curves II

Ejercicio\(\PageIndex{2}\)

Encontrar el área de una región entre curvas que se cruzan

Ejemplo\(\PageIndex{3}\): Finding the Area of a Region Bounded by Functions That Cross

Ejercicio\(\PageIndex{3}\)

Ejemplo\(\PageIndex{4}\): Finding the Area of a Complex Region

Ejercicio\(\PageIndex{4}\)

Encontrar el área entre dos curvas, integrando a lo largo del eje y

Ejemplo\(\PageIndex{5}\): Integrating with Respect to y

Ejercicio\(\PageIndex{5}\)