6.6E: Ejercicios para la Sección 6.6
- Page ID
- 116187
En los ejercicios 1 - 6, calcular el centro de masa para la recolección de masas dadas.
1)\(m_1=2\) en\(x_1=1\) y\(m_2=4\) en\(x_2=2\)
2)\(m_1=1\) en\(x_1=−1\) y\(m_2=3\) en\(x_2=2\)
- Contestar
- \(x = \frac{5}{4}\)
3)\(m=3\) en\(x=0,1,2,6\)
4) Masas unitarias en\((x,y)=(1,0),(0,1),(1,1)\)
- Contestar
- \(\left(\frac{2}{3},\, \frac{2}{3}\right)\)
5)\(m_1=1\) en\((1,0)\) y\(m_2=4\) en\((0,1)\)
6)\(m_1=1\) en\((1,0)\) y\(m_2=3\) en\((2,2)\)
- Contestar
- \(\left(\frac{7}{4},\,\frac{3}{2}\right)\)
En los ejercicios 7 - 16, computar el centro de masa\(\bar x.\)
7)\(ρ=1\) para\(x∈(−1,3)\)
8)\(ρ=x^2\) para\(x∈(0,L)\)
- Contestar
- \(\dfrac{3L}{4}\)
9)\(ρ=1\) para\(x∈(0,1)\) y\(ρ=2\) para\(x∈(1,2)\)
10)\(ρ=\sin x\) para\(x∈(0,π)\)
- Contestar
- \(\frac{π}{2}\)
11)\(ρ=\cos x\) para\(x∈\left(0,\frac{π}{2}\right)\)
12)\(ρ=e^x\) para\(x∈(0,2)\)
- Contestar
- \(\dfrac{e^2+1}{e^2−1}\)
13)\(ρ=x^3+xe^{−x}\) para\(x∈(0,1)\)
14)\(ρ=x\sin x\) para\(x∈(0,π)\)
- Contestar
- \(\dfrac{π^2−4}{π}\)
15)\(ρ=\sqrt{x}\) para\(x∈(1,4)\)
16)\(ρ=\ln x\) para\(x∈(1,e)\)
- Contestar
- \(\frac{1}{4}(1+e^2)\)
En los ejercicios 17 - 19, computar el centro de masa\((\bar{x},\bar{y}).\) Usa la simetría para ayudar a localizar el centro de masa siempre que sea posible.
17)\(ρ=7\) en la plaza\(0≤x≤1, \; 0≤y≤1\)
18)\(ρ=3\) en el triángulo con vértices\((0,0), \, (a,0)\), y\((0,b)\)
- Contestar
- \(\left(\frac{a}{3},\, \frac{b}{3}\right)\)
19)\(ρ=2\) para la región delimitada por\(y=\cos(x), \; y=−\cos(x), \; x=−\frac{π}{2}\), y\(x=\frac{π}{2}\)
En los ejercicios 20 - 26, usa una calculadora para dibujar la región, luego computar el centro de masa\((\bar{x},\bar{y}).\) Usa la simetría para ayudar a localizar el centro de masa siempre que sea posible.
20) [T] La región delimitada por\(y=\cos(2x), \; x=−\frac{π}{4}\), y\(x=\frac{π}{4}\)
- Contestar
- \(\left(0,\frac{π}{8}\right)\)
21) [T] La región entre\(y=2x^2, \; y=0, \; x=0,\) y\(x=1\)
22) [T] La región entre\(y=\frac{5}{4}x^2\) y\(y=5\)
- Contestar
- \((0,3)\)
23) [T] Región entre\(y=\sqrt{x}, \; y=\ln x, \; x=1,\) y\(x=4\)
24) [T] La región delimitada por\(y=0\) y\(\dfrac{x^2}{4}+\dfrac{y^2}{9}=1\)
- Contestar
- \(\left(0,\frac{4}{π}\right)\)
25) [T] La región delimitada por\(y=0, \; x=0,\) y\(\dfrac{x^2}{4}+\dfrac{y^2}{9}=1\)
26) [T] La región delimitada por\(y=x^2\) y\(y=x^4\) en el primer cuadrante
- Contestar
- \(\left(\frac{5}{8},\, \frac{1}{3}\right)\)
En los ejercicios 27 - 31, utilizar el teorema de Pappus para determinar el volumen de la forma.
27) Girando\(y=mx\) alrededor del\(x\) eje entre\(x=0\) y\(x=1\)
28) Rotación\(y=mx\) alrededor del\(y\) eje entre\(x=0\) y\(x=1\)
- Contestar
- \(V = \frac{mπ}{3}\)unidades³
29) Un cono general creado al girar un triángulo con vértices\((0,0), \, (a,0),\) y\((0,b)\) alrededor del\(y\) eje. ¿Tu respuesta concuerda con el volumen de un cono?
30) Un cilindro general creado al girar un rectángulo con vértices\((0,0), \, (a,0), \, (0,b),\) y\((a,b)\) alrededor del\(y\) eje. ¿Su respuesta concuerda con el volumen de un cilindro?
- Contestar
- \(V = πa^2b\)unidades³
31) Una esfera creada al girar un semicírculo con radio\(a\) alrededor del\(y\) eje. ¿Su respuesta concuerda con el volumen de una esfera?
En los ejercicios 32 - 36, utilice una calculadora para dibujar la región encerrada por la curva. Encuentra el área\(M\) y el centroide\((\bar{x},\bar{y})\) para las formas dadas. Utilice la simetría para ayudar a localizar el centro de masa siempre que sea posible.
32) [T] Cuarto de círculo:\(y=\sqrt{1−x^2}, \; y=0\), y\(x=0\)
- Contestar
- \(\left(\frac{4}{3π},\, \frac{4}{3π}\right)\)
33) [T] Triángulo:\(y=x, \; y=2−x\), y\(y=0\)
34) [T] Lente:\(y=x^2\) y\(y=x\)
- Contestar
- \(\left(\frac{1}{2},\, \frac{2}{5}\right)\)
35) [T] Anillo:\(y^2+x^2=1\) y\(y^2+x^2=4\)
36) [T] Medio anillo:\(y^2+x^2=1, \; y^2+x^2=4,\) y\(y=0\)
- Contestar
- \(\left(0,\, \frac{28}{9π}\right)\)
37) Encontrar el centro de masa generalizado en la astillas entre\(y=x^a\) y\(y=x^b\) con\(a>b\). Luego, usa el teorema de Pappus para encontrar el volumen del sólido generado al girar alrededor del\(y\) eje -eje.
38) Encontrar el centro generalizado de masa entre\(y=a^2−x^2, \; x=0\), y\(y=0\). Luego, usa el teorema de Pappus para encontrar el volumen del sólido generado al girar alrededor del\(y\) eje -eje.
- Contestar
- Centro de masa:\(\left(\frac{a}{6},\,\frac{4a^2}{5}\right),\)
Volumen:\(\dfrac{2πa^4}{9}\) unidades³
39) Encuentra el centro de masa generalizado entre\(y=b\sin(ax),\; x=0,\) y\(x=\dfrac{π}{a}.\) Entonces, usa el teorema de Pappus para encontrar el volumen del sólido generado al girar alrededor del\(y\) eje -eje.
40) Usa el teorema de Pappus para encontrar el volumen de un toro (en la foto aquí). Supongamos que un disco de radio\(a\) se posiciona con el extremo izquierdo del círculo en\(x=b, \, b>0,\) y se gira alrededor del\(y\) eje.
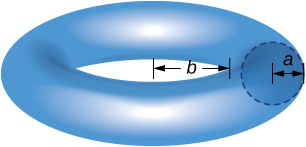
- Contestar
- Volumen:\(V = 2\pi^2a^2(b+a)\)
41) Encuentra el centro de masa\((\bar{x},\bar{y})\) para un cable delgado a lo largo del semicírculo\(y=\sqrt{1−x^2}\) con masa unitaria. (Pista: Usa el teorema de Pappus.)


