6.6: Momentos y Centros de Masa

Última actualización
Guardar como PDF

Page ID: 116183

Edwin “Jed” Herman & Gilbert Strang
OpenStax

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Objetivos de aprendizaje

Encuentra el centro de masa de los objetos distribuidos a lo largo de una línea.
Localice el centro de masa de una placa delgada.
Usa la simetría para ayudar a localizar el centroide de una placa delgada.
Aplicar el teorema de Pappus para volumen.

En esta sección, consideramos centros de masa (también llamados centroides, bajo ciertas condiciones) y momentos. La idea básica del centro de masa es la noción de punto de equilibrio. Muchos de nosotros hemos visto artistas que hacen girar platos en los extremos de palos. Los intérpretes tratan de mantener a varios de ellos girando sin permitir que ninguno de ellos caiga. Si miramos un solo plato (sin girarlo), hay un punto dulce en el plato donde se equilibra perfectamente en el palo. Si ponemos el palo en otro lugar que no sea ese punto dulce, el plato no se equilibra y cae al suelo. (Es por eso que los artistas hacen girar las placas; el giro ayuda a evitar que las placas se caigan incluso si el palo no está exactamente en el lugar correcto). Matemáticamente, ese punto dulce se llama el centro de masa del plato.

En esta sección, primero examinamos estos conceptos en un contexto unidimensional, luego expandimos nuestro desarrollo para considerar centros de masa de regiones bidimensionales y simetría. Por último, utilizamos centroides para encontrar el volumen de ciertos sólidos aplicando el teorema de Pappus.

Centro de Misas y Momentos

Empecemos por mirar el centro de masa en un contexto unidimensional. Considera un alambre o varilla larga y delgada de masa insignificante que descansa sobre un fulcro, como se muestra en la Figura\(\PageIndex{1a}\). Ahora supongamos que colocamos objetos que tienen masas\(m_1\) y\(m_2\) a distancias\(d_1\) y\(d_2\) desde el fulcro, respectivamente, como se muestra en la Figura\(\PageIndex{1b}\).

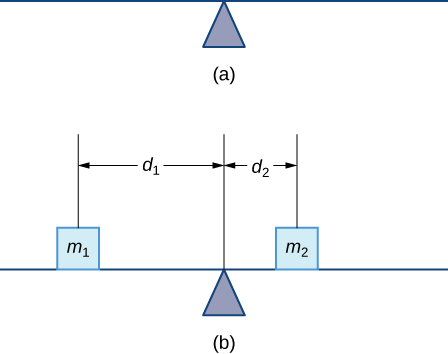
Esta figura tiene dos imágenes. La primera imagen es una línea horizontal en la parte superior de un triángulo equilátero. Representa una varilla sobre un fulcro. La segunda imagen es la misma que la primera con dos cuadrados en la línea. Están etiquetados como msub1 y msub2. La distancia de msub1 al fulcro es dsub1. La distancia de msub2 al fulcro es dsub2. — Figura\(\PageIndex{1}\): (a) Una varilla delgada descansa sobre un fulcro. (b) Se colocan masas sobre la varilla.

El ejemplo más común de la vida real de un sistema como este es un balancín de juegos, o tambalancín, con niños de diferentes pesos sentados a diferentes distancias del centro. En un balancín, si un niño se sienta en cada extremo, el niño más pesado se hunde y el niño más ligero es levantado en el aire. Sin embargo, si el niño más pesado se desliza hacia el centro, el balancín se equilibra. Aplicando este concepto a las masas en la varilla, observamos que las masas se equilibran entre sí si y solo si

\[m_1d_1=m_2d_2. \nonumber \]

Esta figura es una imagen del eje x. En el eje hay un punto etiquetado x barra. También en el eje hay un punto xsub1 con un cuadrado encima del mismo. Dentro del cuadrado se encuentra la etiqueta msub1. También hay un punto xsub2 en el eje. Por encima de este punto hay una plaza. Dentro del cuadrado se encuentra la etiqueta msub2. — Figura\(\PageIndex{2}\): El centro de masa\(\bar{x}\) es el punto de equilibrio del sistema.

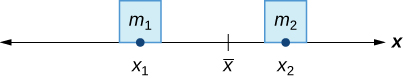
En el ejemplo del balancín, equilibramos el sistema moviendo a las masas (niños) con respecto al fulcro. No obstante, estamos realmente interesados en sistemas en los que no se permita que las masas se muevan, y en cambio equilibramos el sistema moviendo el punto de apoyo. Supongamos que tenemos dos masas puntuales\(m_2\),\(m_1\) y, ubicadas en una recta numérica en puntos\(x_1\) y\(x_2\), respectivamente (Figura\(\PageIndex{2}\)). El centro de masa,\(\bar{x}\), es el punto donde se debe colocar el fulcro para hacer que el sistema se equilibre.

Por lo tanto, tenemos

\[ \begin{align*} m_1|x_1−\bar{x}| &=m_2|x_2−\bar{x}| \\[4pt] m_1(\bar{x}−x_1) &=m_2(x_2−\bar{x}) \\[4pt] m_1\bar{x}−m_1x_1 &=m_2x_2−m_2\bar{x} \\[4pt] \bar{x}(m_1+m_2) &=m_1x_1+m_2x_2 \end{align*} \nonumber \]

\[ \bar{x} =\dfrac{m_1x_1+m_2x_2}{m_1+m_2} \label{COM} \]

La expresión en el numerador de la Ecuación\ ref {COM}\(m_1x_1+m_2x_2\),, se llama el primer momento del sistema con respecto al origen. Si el contexto es claro, a menudo soltamos la palabra primero y solo nos referimos a esta expresión como el momento del sistema. La expresión en el denominador,\(m_1+m_2\), es la masa total del sistema. Así, el centro de masa del sistema es el punto en el que se podría concentrar la masa total del sistema sin cambiar el momento.

Esta idea no se limita sólo a dos masas puntuales. En general, si\(n\) las masas, se\(m_1,m_2,…,m_n,\) colocan en una recta numérica en puntos\(x_1,x_2,…,x_n,\) respectivamente, entonces el centro de masa del sistema viene dado por

\[ \bar{x}=\dfrac{\displaystyle {\sum_{i=1}^nm_ix_i}}{\displaystyle {\sum_{i=1}^nm_i}} \nonumber \]

Centro de masa de objetos en una línea

Let\(m_1,m_2,…,m_n\) Ser masas puntuales colocadas en una recta numérica en puntos\(x_1,x_2,…,x_n\), respectivamente, y dejar\(\displaystyle m=\sum_{i=1}^nm_i\) denotar la masa total del sistema. Entonces, el momento del sistema con respecto al origen viene dado por

\[M=\sum_{i=1}^nm_ix_i \label{moment} \]

y el centro de masa del sistema viene dado por

\[\bar{x}=\dfrac{M}{m}. \label{COM2a} \]

Aplicamos este teorema en el siguiente ejemplo.

Ejemplo\(\PageIndex{1}\): Finding the Center of Mass of Objects along a Line

Supongamos que se colocan cuatro masas de puntos en una recta numérica como sigue:

\(m_1=30\,kg,\)colocado en\(x_1=−2m\)
\(m_2=5\,kg,\)colocado en\(x_2=3m\)
\(m_3=10\,kg,\)colocado en\(x_3=6m\)
\(m_4=15\,kg,\)colocado en\(x_4=−3m.\)

Solución

Encuentra el momento del sistema con respecto al origen y encuentra el centro de masa del sistema.

Primero, necesitamos calcular el momento del sistema (Ecuación\ ref {momento}):

\[ \begin{align*} M &=\sum_{i=1}^4m_ix_i \\[4pt] &= −60+15+60−45 \\[4pt] &=−30. \end{align*}\]

Ahora, para encontrar el centro de masa, necesitamos la masa total del sistema:

\[ \begin{align*} m &=\sum_{i=1}^4m_i \\[4pt] &=30+5+10+15 \\[4pt] &= 60\, kg \end{align*}\]

Entonces tenemos (de la Ecuación\ ref {Com2a})

\(\bar{x}–=\dfrac{M}{m}=−\dfrac{30}{60}=−\dfrac{1}{2}\).

El centro de masa se ubica 1/2 m a la izquierda del origen.

Ejercicio\(\PageIndex{1}\)

Supongamos que se colocan cuatro masas de puntos en una recta numérica como sigue:

\(m_1=12\,kg\)colocado en\(x_1=−4m\)
\(m_2=12\,kg\)colocado en\(x_2=4m\)
\(m_3=30\,kg\)colocado en\(x_3=2m\)
\(m_4=6\,kg,\)colocado en\(x_4=−6m.\)

Encuentra el momento del sistema con respecto al origen y encuentra el centro de masa del sistema.

Pista: Utilice el proceso del ejemplo anterior.

Contestar: \(M=24,\bar{x}=\dfrac{2}{5}m\)

Podemos generalizar este concepto para encontrar el centro de masa de un sistema de masas puntuales en un plano. Dejar\(m_1\) ser una masa puntual ubicada en punto\((x_1,y_1)\) en el plano. Entonces el momento\(M_x\) de la masa con respecto al\(x\) -eje viene dado por\(M_x=m_1y_1\). Del mismo modo, el momento\(M_y\) con respecto al\(y\) eje viene dado por

\[M_y=m_1x_1. \nonumber \]

Observe que la\(x\) coordenada -del punto se utiliza para calcular el momento con respecto al\(y\) eje -y viceversa. La razón es que la\(x\) coordenada -da la distancia desde la masa puntual hasta el\(y\) eje -eje, y la\(y\) coordenada -da la distancia al\(x\) eje -eje (ver la siguiente figura).

Si tenemos varias masas puntuales en el\(xy\) plano, podemos usar los momentos con respecto a los\(y\) ejes\(x\) - y -para calcular las\(y\) coordenadas\(x\) - y -del centro de masa del sistema.

Centro de masa de objetos en un plano

Dejar\(m_1\),\(m_2\),...,\(m_n\) ser masas puntuales ubicadas en el\(xy\) plano -en puntos\((x_1,y_1),(x_2,y_2),…,(x_n,y_n),\) respectivamente, y dejar\(\displaystyle m=\sum_{i=1}^nm_i\) denotar la masa total del sistema. Entonces los momentos\(M_x\) y\(M_y\) del sistema con respecto a los\(y\) ejes\(x\) - y -respectivamente, están dados por

\[M_x=\sum_{i=1}^nm_iy_i \label{COM1} \]

\[M_y=\sum_{i=1}^nm_ix_i. \label{COM2} \]

Además, las coordenadas del centro de masa\((\bar{x},\bar{y})\) del sistema son

\[\bar{x}=\dfrac{M_y}{m} \label{COM3} \]

\[\bar{y}=\dfrac{M_x}{m}. \label{COM4} \]

El siguiente ejemplo demuestra cómo se pueden aplicar fórmulas al centro de masa (Ecuaciones\ ref {COM1} -\ ref {COM4}).

Ejemplo\(\PageIndex{2}\): Finding the Center of Mass of Objects in a Plane

Supongamos que tres masas puntuales se colocan en el\(xy\) plano de la siguiente manera (supongamos que las coordenadas se dan en metros):

\(m_1=2\,kg\)colocado en\((−1,3),\)
\(m_2=6\,kg\)colocado en\((1,1),\)
\(m_3=4\,kg\)colocado en\((2,−2).\)

Encuentra el centro de masa del sistema.

Solución

Primero calculamos la masa total del sistema:

\[m=\sum_{i=1}^3m_i=2+6+4=12\,kg. \nonumber \]

A continuación encontramos los momentos con respecto a los ejes\(x\) - y\(y\) -ejes:

\[\begin{align*} M_y &=\sum_{i=1}^3m_ix_i=−2+6+8=12, \\[4pt] M_x &=\sum_{i=1}^3m_iy_i=6+6−8=4. \end{align*}\]

Entonces tenemos

\[\bar{x}=\dfrac{M_y}{m}=\dfrac{12}{12}=1 \nonumber \]

\[\bar{y}=\dfrac{M_x}{m}=\dfrac{4}{12}=\dfrac{1}{3}. \nonumber \]

El centro de masa del sistema está\((1,1/3),\) en metros.

Ejercicio\(\PageIndex{2}\)

Supongamos que se colocan tres masas puntuales en una recta numérica de la siguiente manera (supongamos que las coordenadas se dan en metros)

\(m_1=5\,kg,\)colocado en\((−2,−3),\)
\(m_2=3\, kg,\)colocado en\((2,3),\)
\(m_3=2\, kg,\)colocado en\((−3,−2).\)

Encuentra el centro de masa del sistema.

Pista: Utilice el proceso del ejemplo anterior.

Contestar: \((−1,−1)\)m

Centro de masa de placas delgadas

Hasta el momento hemos mirado sistemas de masas puntuales en una línea y en un plano. Ahora, en lugar de tener la masa de un sistema concentrada en puntos discretos, queremos mirar sistemas en los que la masa del sistema se distribuye continuamente a través de una delgada lámina de material. Para nuestros fines, asumimos que la lámina es lo suficientemente delgada como para que pueda tratarse como si fuera bidimensional. Tal hoja se llama lámina. A continuación desarrollamos técnicas para encontrar el centro de masa de una lámina. En esta sección, también asumimos que la densidad de la lámina es constante.

Las láminas suelen estar representadas por una región bidimensional en un plano. El centro geométrico de tal región se llama su centroide. Como hemos asumido que la densidad de la lámina es constante, el centro de masa de la lámina depende únicamente de la forma de la región correspondiente en el plano; no depende de la densidad. En este caso, el centro de masa de la lámina corresponde al centroide de la región delineada en el plano. Al igual que con los sistemas de masas puntuales, necesitamos encontrar la masa total de la lámina, así como los momentos de la lámina con respecto a los ejes\(x\) - y\(y\) -ejes.

Primero consideramos una lámina en forma de rectángulo. Recordemos que el centro de masa de una lámina es el punto donde la lámina se equilibra. Para un rectángulo, ese punto es tanto el centro horizontal como el vertical del rectángulo. A partir de esta comprensión, es claro que el centro de masa de una lámina rectangular es el punto donde se cruzan las diagonales, lo que es resultado del principio de simetría, y aquí se afirma sin pruebas.

El principio de simetría

Si una región\(R\) es simétrica alrededor de una línea\(l\), entonces el centroide de\(R\) se encuentra en\(l\).

Pasemos a las láminas más generales. Supongamos que tenemos una lámina delimitada arriba por la gráfica de una función continua\(f(x)\), abajo por el\(x\) eje -y a la izquierda y a la derecha por las líneas\(x=a\) y\(x=b\), respectivamente, como se muestra en la siguiente figura.

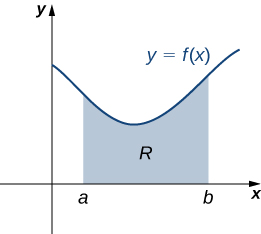
Esta imagen es una gráfica de y=f (x). Está en el primer cuadrante. Bajo la curva hay una región sombreada etiquetada como “R”. La región sombreada está delimitada a la izquierda en x=a y a la derecha en x=b. — Figura\(\PageIndex{4}\): Una región en el plano que representa una lámina.

Al igual que con los sistemas de masas puntuales, para encontrar el centro de masa de la lámina, necesitamos encontrar la masa total de la lámina, así como los momentos de la lámina con respecto a los ejes\(x\) - y\(y\) -ejes. Como lo hemos hecho muchas veces antes, aproximamos estas cantidades particionando el intervalo\([a,b]\) y construyendo rectángulos.

Para\(i=0,1,2,…,n,\) dejar\(P={x_i}\) ser una partición regular de\([a,b]\). Recordemos que podemos elegir cualquier punto dentro del intervalo\([x_{i−1},x_i]\) como nuestro\(x^∗_i\). En este caso, queremos\(x^∗_i\) ser la coordenada x del centroide de nuestros rectángulos. Así, para\(i=1,2,…,n\), seleccionamos\(x^∗_i∈[x_{i−1},x_i]\) tal que\(x^∗_i\) sea el punto medio del intervalo. Es decir,\(x^∗_i=(x_{i−1}+x_i)/2\). Ahora, para\(i=1,2,…,n,\) construir un rectángulo de altura\(f(x^∗_i)\) en\([x_{i−1},x_i].\) El centro de masa de este rectángulo es\((x^∗_i,(f(x^∗_i))/2),\) como se muestra en la siguiente figura.

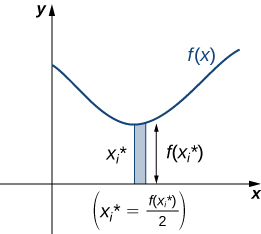
Esta figura es una gráfica de la curva etiquetada f (x). Está en el primer cuadrante. Debajo de la curva y por encima del eje x hay un rectángulo sombreado vertical. la altura del rectángulo se etiqueta f (xsubi). Además, xsubi = f (xsubi/2). — Figura\(\PageIndex{5}\): Rectángulo representativo de la lámina.

A continuación, necesitamos encontrar la masa total del rectángulo. Dejar\(ρ\) representar la densidad de la lámina (nota que\(ρ\) es una constante). En este caso,\(ρ\) se expresa en términos de masa por unidad de superficie. Así, para encontrar la masa total del rectángulo, multiplicamos el área del rectángulo por\(ρ\). Entonces, la masa del rectángulo viene dada por\(ρf(x^∗_i)Δx\).

Para obtener la masa aproximada de la lámina, agregamos las masas de todos los rectángulos para obtener

\[m≈\sum_{i=1}^nρf(x^∗_i)Δx. \label{eq51} \]

La ecuación\ ref {eq51} es una suma de Riemann. Tomando el límite como\(n→∞\) da la masa exacta de la lámina:

\[ \begin{align*} m &=\lim_{n→∞}\sum_{i=1}^nρf(x^∗_i)Δx \\[4pt] &=ρ∫^b_af(x)dx. \end{align*}\]

A continuación, calculamos el momento de la lámina con respecto al eje x. Volviendo al rectángulo representativo, recordar su centro de masa es\((x^∗_i,(f(x^∗_i))/2)\). Recordemos también que tratar el rectángulo como si se tratara de una masa puntual ubicada en el centro de masa no cambia el momento. Así, el momento del rectángulo con respecto al eje x viene dado por la masa del rectángulo,\(ρf(x^∗_i)Δx\), multiplicado por la distancia desde el centro de masa al eje x:\((f(x^∗_i))/2\). Por lo tanto, el momento con respecto al eje x del rectángulo es\(ρ([f(x^∗_i)]^2/2)Δx.\) Sumando los momentos de los rectángulos y tomando el límite de la suma resultante de Riemann, vemos que el momento de la lámina con respecto al eje x es

\[ \begin{align*}M_x &=\lim_{n→∞}\sum_{i=1}^nρ\dfrac{[f(x^∗_i)]^2}{2}Δx \\[4pt] &=ρ∫^b_a\dfrac{[f(x)]^2}{2}dx.\end{align*}\]

Derivamos el momento con respecto al eje y de manera similar, señalando que la distancia desde el centro de masa del rectángulo al eje y es\(x^∗_i\). Entonces el momento de la lámina con respecto al eje y viene dado por

\[ \begin{align*}M_y &=\lim_{n→∞}\sum_{i=1}^nρx^∗_if(x^∗)i)Δx\\[4pt] &=ρ∫^b_axf(x)dx.\end{align*}\]

Encontramos las coordenadas del centro de masa dividiendo los momentos por la masa total para dar\(\bar{x}=M_y/m\) y\(\bar{y}=M_x/m\). Si miramos de cerca las expresiones para\(M_x,M_y\), y\(m\), notamos que la constante se\(ρ\) cancela cuando\(\bar{x}\) y\(\bar{y}\) se calculan.

Resumimos estos hallazgos en el siguiente teorema.

Centro de masa de una placa delgada en el plano XY

Que R denote una región delimitada arriba por la gráfica de una función continua\(f(x)\), abajo por el eje x, y a la izquierda y a la derecha por las líneas\(x=a\) y\(x=b\), respectivamente. Dejar\(ρ\) denotar la densidad de la lámina asociada. Entonces podemos hacer las siguientes declaraciones:

La masa de la lámina es\[m=ρ∫^b_af(x)dx. \label{eq4a} \]
Los momentos\(M_x\) y\(M_y\) de la lámina con respecto a los ejes x e y, respectivamente, son\[M_x=ρ∫^b_a\dfrac{[f(x)]^2}{2}dx\label{eq4b} \] y\[M_y=ρ∫^b_axf(x)dx.\label{eq4c} \]
Las coordenadas del centro de masa\((\bar{x},\bar{y})\) son\[\bar{x}=\dfrac{M_y}{m} \label{eq4d} \] y\[\bar{y}=\dfrac{M_x}{m}. \label{eq4e} \]

En el siguiente ejemplo, utilizamos este teorema para encontrar el centro de masa de una lámina.

Ejemplo\(\PageIndex{3}\): Finding the Center of Mass of a Lamina

Sea R la región delimitada arriba por la gráfica de la función\(f(x)=\sqrt{x}\) y por debajo por el eje x sobre el intervalo\([0,4]\). Encuentra el centroide de la región.

Solución

La región se representa en la siguiente figura.

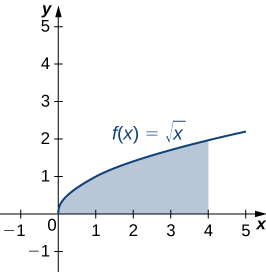
Esta figura es la gráfica de la curva f (x) =squareroot (x). Se trata de una curva creciente en el primer cuadrante. Bajo la curva sobre el eje x hay una región sombreada. Comienza en x=0 y está delimitado a la derecha en x=4. — Figura\(\PageIndex{6}\): Encontrar el centro de masa de una lámina.

Dado que solo se nos pide el centroide de la región, en lugar de la masa o momentos de la lámina asociada, sabemos que la constante de densidad se\(ρ\) cancela de los cálculos eventualmente. Por lo tanto, en aras de la conveniencia, supongamos\(ρ=1\).

Primero, necesitamos calcular la masa total (Ecuación\ ref {eq4a}):

\[ \begin{align*} m &=ρ∫^b_af(x)dx \\[4pt] &=∫^4_0\sqrt{x}dx \\[4pt] &=\dfrac{2}{3}x^{3/2}∣^4_0 \\[4pt] &=\dfrac{2}{3}[8−0] \\[4pt] &=\dfrac{16}{3}. \end{align*}\]

A continuación, calculamos los momentos (Ecuación\ ref {eq4d}):

\[ \begin{align*} M_x &=ρ∫^b_a\dfrac{[f(x)]^2}{2}dx \\[4pt] &=∫^4_0\dfrac{x}{2}dx \\[4pt] &=\dfrac{1}{4}x^2∣^4_0 \\[4pt] &=4 \end{align*}\]

y (Ecuación\ ref {eq4c}):

\[ \begin{align*} M_y &=ρ∫^b_axf(x)dx \\[4pt] &=∫^4_0x\sqrt{x}dx \\[4pt] &=∫^4_0x^{3/2}dx \\[4pt] &=\dfrac{2}{5}x^{5/2}∣^4_0 \\[4pt] &=\dfrac{2}{5}[32−0] \\[4pt] &=\dfrac{64}{5}. \end{align*}\]

Así, tenemos (Ecuación\ ref {eq4d}):

\[ \begin{align*} \bar{x} &=\dfrac{M_y}{m} \\[4pt] &=\dfrac{64/5}{16/3} \\[4pt] &=\dfrac{64}{5}⋅\dfrac{3}{16} \\[4pt] &=\dfrac{12}{5} \end{align*}\]

y (Ecuación\ ref {eq4e}):

\[ \begin{align*} \bar{y} &=\dfrac{M_x}{y} \\[4pt] &=\dfrac{4}{16/3} \\[4pt] &=4⋅\dfrac{3}{16} \\[4pt] &=\dfrac{3}{4}. \end{align*}\]

El centroide de la región es\((12/5,3/4).\)

Ejercicio\(\PageIndex{3}\)

Dejar\(R\) ser la región delimitada arriba por la gráfica de la función\(f(x)=x^2\) y abajo por el eje x sobre el intervalo\([0,2].\) Encuentra el centroide de la región.

Pista: Utilice el proceso del ejemplo anterior.

Contestar: El centroide de la región es\((3/2,6/5).\)

Podemos adaptar este enfoque para encontrar centroides de regiones más complejas también. Supongamos que nuestra región está delimitada arriba por la gráfica de una función continua\(f(x)\), como antes, pero ahora, en lugar de tener el límite inferior para la región sea el eje x, supongamos que la región está delimitada por debajo por la gráfica de una segunda función continua,\(g(x)\), como se muestra en la Figura\(\PageIndex{7}\).

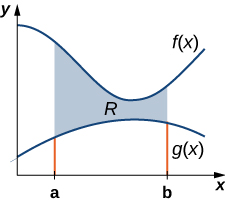
Esta figura es una gráfica del primer cuadrante. Tiene dos curvas. Están etiquetados f (x) y g (x). f (x) está por encima de g (x). Entre las curvas hay una región sombreada etiquetada como “R”. La región sombreada está delimitada a la izquierda por x=a y a la derecha por x=b. — Figura\(\PageIndex{7}\): Una región entre dos funciones.

Nuevamente, particionamos el intervalo\([a,b]\) y construimos rectángulos. En la Figura se muestra un rectángulo representativo\(\PageIndex{8}\).

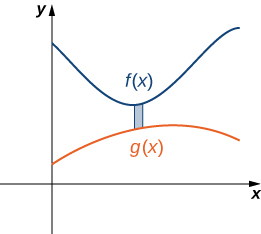
Esta figura es una gráfica del primer cuadrante. Tiene dos curvas. Están etiquetados f (x) y g (x). f (x) está por encima de g (x). Entre las curvas hay un rectángulo sombreado. — Figura\(\PageIndex{8}\): Un rectángulo representativo de la región entre dos funciones.

Tenga en cuenta que el centroide de este rectángulo es\((x^∗_i,(f(x^∗_i)+g(x^∗_i))/2)\). No vamos a pasar por todos los detalles del desarrollo de la suma de Riemann, pero veamos algunos de los pasos clave. En el desarrollo de las fórmulas para la masa de la lámina y el momento con respecto al eje y, la altura de cada rectángulo viene dada por\(f(x^∗_i)−g(x^∗_i)\), lo que lleva a la expresión\(f(x)−g(x)\) en los integrandos.

En el desarrollo de la fórmula por el momento con respecto al eje x, el momento de cada rectángulo se encuentra multiplicando el área del rectángulo,\(ρ[f(x^∗_i)−g(x^∗_i)]Δx,\) por la distancia del centroide desde el\(x\) eje -eje,\((f(x^∗_i)+g(x^∗_i))/2\), lo que da\(ρ(1/2){[f(x^∗_i)]^2−[g(x^∗_i)]^2}Δx\). Resumiendo estos hallazgos, llegamos al siguiente teorema.

Centro de Masa de una Lámina Limitada por Dos Funciones

Dejar\(R\) denotar una región delimitada arriba por la gráfica de una función continua\(f(x),\) a continuación por la gráfica de la función continua\(g(x)\), y a la izquierda y a la derecha por las líneas\(x=a\) y\(x=b\), respectivamente. Dejar\(ρ\) denotar la densidad de la lámina asociada. Entonces podemos hacer las siguientes declaraciones:

La masa de la lámina es\[m=ρ∫^b_a[f(x)−g(x)]dx. \nonumber \]
Los momentos\(M_x\) y\(M_y\) de la lámina con respecto a los ejes x e y, respectivamente, son\[M_x=ρ∫^b_a12([f(x)]^2−[g(x)]^2)dx \nonumber \] y\[M_y=ρ∫^b_ax[f(x)−g(x)]dx. \nonumber \]
Las coordenadas del centro de masa\(\bar{x},\bar{y})\) son\[\bar{x}=\dfrac{M_y}{m} \nonumber \] y\[\bar{y}=\dfrac{M_x}{m} \nonumber \]

Ilustramos este teorema en el siguiente ejemplo.

Ejemplo\(\PageIndex{4}\): Finding the Centroid of a Region Bounded by Two Functions

Sea R la región delimitada arriba por la gráfica de la función\(f(x)=1−x^2\) y abajo por la gráfica de la función\(g(x)=x−1.\) Encuentra el centroide de la región.

Solución

La región se representa en la siguiente figura.

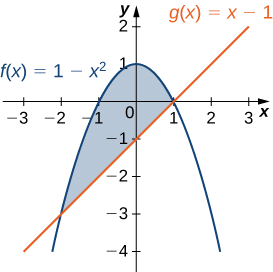
Esta figura es una gráfica. Tiene dos curvas. Se etiquetan con f (x) =1-x^2 y g (x) =x-1. Entre las curvas hay una región sombreada. La región sombreada está delimitada a la izquierda por x=a y a la derecha por x=b. — Figura\(\PageIndex{9}\): Encontrar el centroide de una región entre dos curvas.

Las gráficas de las funciones se cruzan en\((−2,−3)\) y\((1,0)\), así integramos de −2 a 1. Una vez más, en aras de la conveniencia, asumamos\(ρ=1\).

Primero, necesitamos calcular la masa total:

\[ \begin{align*} m &=ρ∫^b_a[f(x)−g(x)]dx \\[4pt] &=∫^1_{−2}[1−x^2−(x−1)]dx \\[4pt] &=∫^1_{−2}(2−x^2−x)dx \\[4pt] &=\left[2x−\dfrac{1}{3}x^3−\dfrac{1}{2}x^2\right]∣^1_{−2} \\[4pt] &=\left[2−\dfrac{1}{3}−\dfrac{1}{2}\right]−\left[−4+\dfrac{8}{3}−2\right]\\[4pt] &=\dfrac{9}{2}. \end{align*}\]

A continuación, calculamos los momentos:

\[ \begin{align*} M_x&=ρ∫^b_a\dfrac{1}{2}([f(x)]^2−[g(x)]^2)dx \\[4pt] &=\dfrac{1}{2}∫^1_{−2}((1−x^2)^2−(x−1)^2)dx\\[4pt] &=\dfrac{1}{2}∫^1_{−2}(x^4−3x^2+2x)dx \\[4pt] &=\dfrac{1}{2} \left[\dfrac{x^5}{5}−x^3+x^2\right]∣^1_{−2}\\[4pt] &=−\dfrac{27}{10} \end{align*}\]

\[ \begin{align*} M_y &=ρ∫^b_ax[f(x)−g(x)]dx \\[4pt] &=∫^1_{−2}x[(1−x^2)−(x−1)]dx\\[4pt] &=∫^1_{−2}x[2−x^2−x]dx\\[4pt] &=∫^1_{−2}(2x−x^4−x^2)dx \\[4pt] &=\left[x^2−\dfrac{x^5}{5}−\dfrac{x^3}{3}\right]∣^1_{−2}\\[4pt] &=−\dfrac{9}{4}. \end{align*}\]

Por lo tanto, tenemos

\[ \begin{align*} \bar{x} &=\dfrac{M_y}{m}\\[4pt] &=−\dfrac{9}{4}⋅\dfrac{2}{9}\\[4pt] &=−\dfrac{1}{2} \end{align*}\]

\[ \begin{align*} \bar{y} &=\dfrac{M_x}{y}\\[4pt] &=−\dfrac{27}{10}⋅\dfrac{2}{9}\\[4pt] &=−\dfrac{3}{5}. \end{align*}\]

El centroide de la región es\((−(1/2),−(3/5)).\)

Ejercicio\(\PageIndex{4}\)

Dejar\(R\) ser la región delimitada arriba por la gráfica de la función\(f(x)=6−x^2\) y abajo por la gráfica de la función\(g(x)=3−2x.\) Encuentra el centroide de la región.

Pista: Utilice el proceso del ejemplo anterior.

Contestar: El centroide de la región es\((1,13/5).\)

El principio de simetría

Declaramos el principio de simetría antes, cuando estábamos mirando el centroide de un rectángulo. El principio de simetría puede ser de gran ayuda a la hora de encontrar centroides de regiones que son simétricas. Considera el siguiente ejemplo.

Ejemplo\(\PageIndex{5}\): Finding the Centroid of a Symmetric Region

Sea R la región delimitada arriba por la gráfica de la función\(f(x)=4−x^2\) y abajo por el eje x. Encuentra el centroide de la región.

Solución

La región se representa en la siguiente figura

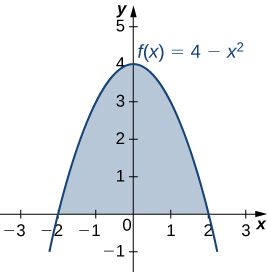
Esta figura es una gráfica de la función f (x) =4-x^2. Es una parábola boca abajo. La región debajo de la parábola sobre el eje x está sombreada. La curva cruza el eje x en x=-2 y x=2. — Figura\(\PageIndex{10}\): Podemos utilizar el principio de simetría para ayudar a encontrar el centroide de una región simétrica.

La región es simétrica con respecto al eje y. Por lo tanto, la coordenada x del centroide es cero. Sólo necesitamos calcular\(\bar{y}\). Una vez más, en aras de la conveniencia, asumamos\(ρ=1\).

Primero, calculamos la masa total:

\[ \begin{align*} m &=ρ∫^b_af(x)dx \\[4pt] &=∫^2_{−2}(4−x^2)dx \\[4pt] &=\left[4x−\dfrac{x^3}{3}\right]∣^2_{−2} \\[4pt] &=\dfrac{32}{3}. \end{align*}\]

A continuación, calculamos los momentos. Solo necesitamos\(M_x\):

\[ \begin{align*} M_x &=ρ∫^b_a\dfrac{[f(x)]^2}{2}dx \\[4pt] &=\dfrac{1}{2}∫^2_{−2}\left[4−x^2\right]^2dx =\dfrac{1}{2}∫^2_{−2}(16−8x^2+x^4)dx \\[4pt] &=\dfrac{1}{2}\left[\dfrac{x^5}{5}−\dfrac{8x^3}{3}+16x\right]∣^2_{−2}=\dfrac{256}{15} \end{align*}\]

Entonces tenemos

\[\bar{y}=\dfrac{M_x}{y}=\dfrac{256}{15}⋅\dfrac{3}{32}=\dfrac{8}{5}. \nonumber \]

El centroide de la región es\((0,8/5).\)

Ejercicio\(\PageIndex{5}\)

Dejar\(R\) ser la región delimitada arriba por la gráfica de la función\(f(x)=1−x^2\) y abajo por\(x\) -eje. Encuentra el centroide de la región.

Pista: Utilice el proceso del ejemplo anterior.

Contestar: El centroide de la región es\((0,2/5).\)

El Skywalk del Gran Cañón

El Grand Canyon Skywalk abrió al público el 28 de marzo de 2007. Esta maravilla de ingeniería es una plataforma de observación en forma de herradura suspendida 4000 pies sobre el río Colorado en el borde oeste del Gran Cañón. Su piso de vidrio cristalino permite impresionantes vistas del cañón de abajo (ver la siguiente figura).

El Skywalk es un diseño en voladizo, lo que significa que la plataforma de observación se extiende sobre el borde del cañón, sin medios visibles de soporte debajo de él. A pesar de la falta de postes de soporte o puntales visibles, las estructuras en voladizo están diseñadas para ser muy estables y el Skywalk no es la excepción. La plataforma de observación está firmemente unida a los postes de soporte que se extienden 46 pies hacia abajo hasta el lecho rocoso. La estructura fue construida para soportar vientos de 100 mph y un terremoto de magnitud 8.0 dentro de 50 mi, y es capaz de soportar más de 70,000,000 lb.

Un factor que afecta la estabilidad del Skywalk es el centro de gravedad de la estructura. Vamos a calcular el centro de gravedad del Skywalk, y examinar cómo cambia el centro de gravedad cuando los turistas salen a la plataforma de observación.

La plataforma de observación tiene forma de U. Las patas de la U miden 10 pies de ancho y comienzan en tierra, debajo del centro de visitantes, a 48 pies del borde del cañón. La plataforma se extiende 70 pies sobre el borde del cañón.

Para calcular el centro de masa de la estructura, la tratamos como una lámina y utilizamos una región bidimensional en el plano xi para representar la plataforma. Comenzamos dividiendo la región en tres subregiones para que podamos considerar cada subregión por separado. La primera región, denotada\(R_1\), consiste en la parte curva de la U. Modelamos\(R_1\) como un anillo semicircular, con radio interior 25 pies y radio exterior 35 pies, centrado en el origen (Figura\(\PageIndex{12}\)).

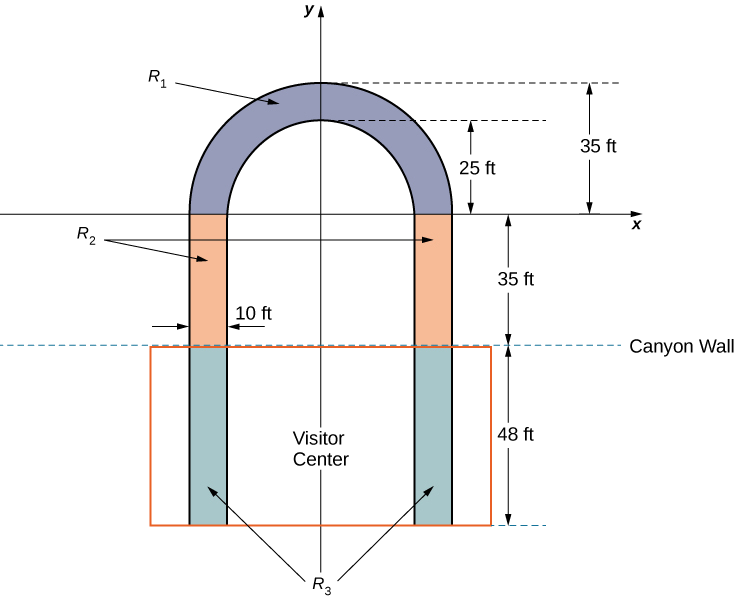
Esta figura es un boceto de la pasarela del Gran Cañón. Está en el sistema de coordenadas xy. La pasarela tiene forma de “u” al revés. Se ha dividido en tres regiones. La primera región en la parte superior está etiquetada como “Rsub1”. Es un semicírculo con radio exterior de 35 pies y radio interior de 25 pies. La segunda región está etiquetada como “Rsub2”. Tiene dos rectángulos con ancho de 10 pies cada uno y altura de 35 pies. La tercera región está etiquetada como “Rsub3” y es de dos rectángulos. Tienen un ancho de 10 pies y una altura de 48 pies. Estos representan la parte de la pasarela dentro del centro de visitantes. — Figura\(\PageIndex{12}\): Modelamos el Skywalk con tres subregiones.

Las patas de la plataforma, que se extienden 35 pies entre\(R_1\) y la pared del cañón, comprenden la segunda subregión,\(R_2\). Por último, los extremos de las piernas, que se extienden 48 pies bajo el centro de visitantes, comprenden la tercera subregión,\(R_3\). Asumir que la densidad de la lámina es constante y asumir que el peso total de la plataforma es de 1,200,000 lb (sin incluir el peso del centro de visitantes; lo consideraremos más adelante). Uso\(g=32\;ft/sec^2\).

Calcular el área de cada una de las tres subregiones. Tenga en cuenta que las áreas de regiones\(R_2\) y\(R_3\) deben incluir únicamente las áreas de las patas, no el espacio abierto entre ellas. Respuestas redondas al pie cuadrado más cercano.
Determinar la masa asociada a cada una de las tres subregiones.
Calcular el centro de masa de cada una de las tres subregiones.
Ahora, tratar cada una de las tres subregiones como una masa puntual ubicada en el centro de masa de la subregión correspondiente. Usando esta representación, calcula el centro de masa de toda la plataforma.
Supongamos que el centro de visitantes pesa 2,200,000 lb, con un centro de masa correspondiente al centro de masa de\(R_3\) .Tratando el centro de visitantes como una masa puntual, recalcular el centro de masa del sistema. ¿Cómo cambia el centro de masa?
Si bien el Skywalk fue construido para limitar el número de personas en la plataforma de observación a 120, la plataforma es capaz de soportar hasta 800 personas que pesan 200 lb cada una. Si todas las 800 personas estuvieran permitidas en la plataforma, y todas ellas fueran al extremo más alejado de la plataforma, ¿cómo se afectaría el centro de gravedad del sistema? (Incluya el centro de visitantes en los cálculos y represente a las personas por una masa puntual ubicada en el borde más alejado de la plataforma, a 70 pies de la pared del cañón).

Teorema de Pappus

Esta sección termina con una discusión del teorema de Pappus para volumen, lo que nos permite encontrar el volumen de tipos particulares de sólidos mediante el uso del centroide. (También hay un teorema de Pappus para la superficie, pero es mucho menos útil que el teorema para el volumen.)

Teorema de Pappus para Volumen

Dejar\(R\) ser una región en el plano y dejar que l sea una línea en el plano que no se cruza\(R\). Entonces el volumen del sólido de revolución formado al girar\(R\) alrededor de l es igual al área de\(R\) multiplicado por la distancia d recorrida por el centroide de\(R\).

Prueba

Podemos probar el caso cuando la región está delimitada arriba por la gráfica de una función\(f(x)\) y por debajo por la gráfica de una función\(g(x)\) sobre un intervalo\([a,b]\), y para lo cual el eje de revolución es el\(y\) eje -eje. En este caso, la zona de la región es\(\displaystyle A=∫^b_a[f(x)−g(x)]\,dx\). Dado que el eje de rotación es el\(y\) eje -eje, la distancia recorrida por el centroide de la región depende únicamente de la\(x\) coordenada -del centroide\(\bar{x}\), que es

\[x=\dfrac{M_y}{m}, \nonumber \]

donde

\[m=ρ∫^b_a[f(x)−g(x)]dx \nonumber \]

\[M_y=ρ∫^b_ax[f(x)−g(x)]dx. \nonumber \]

Entonces,

\[d=2π\dfrac{\displaystyle {ρ∫^b_ax[f(x)−g(x)]dx}}{\displaystyle{ρ∫^b_a[f(x)−g(x)]dx}} \nonumber \]

y por lo tanto

\[d⋅A=2π∫^b_ax[f(x)−g(x)]dx. \nonumber \]

Sin embargo, utilizando el método de conchas cilíndricas, tenemos

\[V=2π∫^b_ax[f(x)−g(x)]dx. \nonumber \]

Entonces,

\[V=d⋅A \nonumber \]

y la prueba está completa.

□

Ejemplo\(\PageIndex{6}\): Using the Theorem of Pappus for Volume

Dejar\(R\) ser un círculo de radio 2 centrado en\((4,0).\) Usa el teorema de Pappus para volumen para encontrar el volumen del toro generado al girar\(R\) alrededor del\(y\) eje -eje.

Solución

La región y el toro se representan en la siguiente figura.

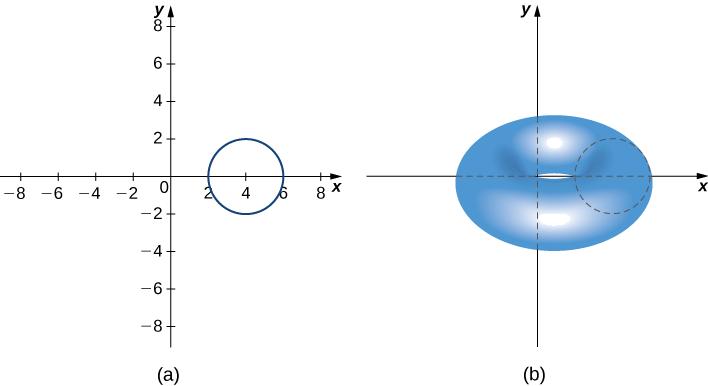
Esta figura tiene dos gráficas. El primero es el sistema de coordenadas x y con un círculo centrado en el eje x en x=4. El radio es 2. La segunda figura es el sistema de coordenadas x y. El círculo de la primera imagen se ha girado alrededor del eje y para formar un toro. — Figura\(\PageIndex{13}\): Determinar el volumen de un toro usando el teorema de Pappus. (a) Una región circular\(R\) en el plano; (b) el toro generado al girar\(R\) alrededor del\(y\) eje.

La región\(R\) es un círculo de radio 2, por lo que el área de R es\(A=4π\;\text{units}^2\). Por el principio de simetría, el centroide de R es el centro del círculo. El centroide se desplaza alrededor del\(y\) eje en una trayectoria circular de radio 4, por lo que el centroide viaja\(d=8π\) unidades. Entonces, el volumen del toro es\(A⋅d=32π^2\) unidades ³.

Ejercicio\(\PageIndex{6}\)

Que R sea un círculo de radio 1 centrado en\((3,0).\) Usa el teorema de Pappus para volumen para encontrar el volumen del toro generado al girar R alrededor del\(y\) eje -eje.

Pista: Utilice el proceso del ejemplo anterior.

Contestar: \(6π^2\)unidades ³

Conceptos clave

Matemáticamente, el centro de masa de un sistema es el punto en el que la masa total del sistema podría concentrarse sin cambiar el momento. Hablando vagamente, el centro de masa puede considerarse como el punto de equilibrio del sistema.
Para las masas puntuales distribuidas a lo largo de una recta numérica, el momento del sistema con respecto al origen es\(\displaystyle M=\sum^n_{i=1}m_ix_i.\) Para las masas puntuales distribuidas en un plano, los momentos del sistema con respecto a los\(y\) ejes\(x\) - y -respectivamente, son\(\displaystyle M_x=\sum^n_{i=1}m_iy_i\) y\(\displaystyle M_y=\sum^n_{i=}m_ix_i\), respectivamente.
Para una lámina delimitada arriba por una función\(f(x)\), los momentos del sistema con respecto a los\(y\) ejes\(x\) - y -respectivamente, son\(\displaystyle M_x=ρ∫^b_a\dfrac{[f(x)]^2}{2}\,dx\) y\(\displaystyle M_y=ρ∫^b_axf(x)\,dx.\)
Las\(y\) coordenadas\(x\) - y -del centro de masa se pueden encontrar dividiendo los momentos alrededor del\(y\) eje y alrededor del\(x\) eje, respectivamente, por la masa total. El principio de simetría dice que si una región es simétrica con respecto a una línea, entonces el centroide de la región se encuentra en la línea.
El teorema de Pappus para volumen dice que si una región gira alrededor de un eje externo, el volumen del sólido resultante es igual al área de la región multiplicada por la distancia recorrida por el centroide de la región.

Ecuaciones Clave

Masa de una lámina

\(\displaystyle m=ρ∫^b_af(x)dx\)

Momentos de una lámina

\(\displaystyle M_x=ρ∫^b_a\dfrac{[f(x)]^2}{2}\,dx\text{ and }M_y=ρ∫^b_axf(x)\,dx\)

Centro de masa de una lámina

\(\bar{x}=\dfrac{M_y}{m}\text{ and }\bar{y}=\dfrac{M_x}{m}\)

Glosario

centro de masa: el punto en el que la masa total del sistema podría concentrarse sin cambiar el momento

centroide: el centroide de una región es el centro geométrico de la región; las láminas suelen estar representadas por regiones en el plano; si la lámina tiene una densidad constante, el centro de masa de la lámina depende únicamente de la forma de la región plana correspondiente; en este caso, el centro de masa de la lámina corresponde a el centroide de la región representativa

lamina: una lámina delgada de material; las láminas son lo suficientemente delgadas como para que, con fines matemáticos, puedan tratarse como si fueran bidimensionales

momento: si n masas están dispuestas en una recta numérica, el momento del sistema con respecto al origen viene dado por\(\displaystyle M=\sum^n_{i=1}m_ix_i\); si, en cambio, consideramos una región en el plano, delimitada arriba por una función\(f(x)\) sobre un intervalo\([a,b]\), entonces los momentos de la región con respecto al\(x\) - y \(y\)-ejes están dados por\(\displaystyle M_x=ρ∫^b_a\dfrac{[f(x)]^2}{2}\,dx\) y\(\displaystyle M_y=ρ∫^b_axf(x)\,dx\), respectivamente

principio de simetría: el principio de simetría establece que si una región\(R\) es simétrica alrededor de una línea\(I\), entonces el centroide de\(R\) se encuentra en\(I\)

teorema de Pappus para volumen: este teorema establece que el volumen de un sólido de revolución formado al girar una región alrededor de un eje externo es igual al área de la región multiplicado por la distancia recorrida por el centroide de la región