6.7: Integrales, funciones exponenciales y logaritmos
- Page ID
- 116172
- Escribir la definición del logaritmo natural como integral.
- Reconocer la derivada del logaritmo natural.
- Integrar funciones que involucran la función logarítmica natural.
- Definir el número\(e\) a través de una integral.
- Reconocer la derivada e integral de la función exponencial.
- Demostrar propiedades de logaritmos y funciones exponenciales usando integrales.
- Expresar funciones logarítmicas y exponenciales generales en términos de logaritmos naturales y exponenciales.
Ya examinamos funciones exponenciales y logaritmos en capítulos anteriores. Sin embargo, pasamos por alto algunos detalles clave en las discusiones anteriores. Por ejemplo, no estudiamos cómo tratar las funciones exponenciales con exponentes que son irracionales. La definición del número e es otra área donde el desarrollo anterior fue algo incompleto. Ahora tenemos las herramientas para tratar estos conceptos de una manera matemáticamente más rigurosa, y lo hacemos en esta sección.
Para efectos de esta sección, supongamos que aún no hemos definido el logaritmo natural, el número\(e\), o alguna de las fórmulas de integración y diferenciación asociadas a estas funciones. Al final de la sección, habremos estudiado estos conceptos de una manera matemáticamente rigurosa (y veremos que son consistentes con los conceptos que aprendimos anteriormente). Comenzamos la sección definiendo el logaritmo natural en términos de una integral. Esta definición forma la base de la sección. De esta definición, derivamos fórmulas de diferenciación, definimos el número\(e\) y expandimos estos conceptos a logaritmos y funciones exponenciales de cualquier base.
El logaritmo natural como integral
Recordemos la regla de potencia para integrales:
\[ ∫ x^n \,dx = \dfrac{x^{n+1}}{n+1} + C , \quad n≠−1. \nonumber \]
Claramente, esto no funciona cuando\(n=−1,\) ya que nos obligaría a dividirnos por cero. Entonces, ¿con qué hacemos\(\displaystyle ∫\dfrac{1}{x}\,dx\)? Recordemos del Teorema Fundamental del Cálculo que\(\displaystyle ∫^x_1\dfrac{1}{t}dt\) es un antiderivado de\(\dfrac{1}{x}.\) Por lo tanto, podemos hacer la siguiente definición.
Para\(x>0\), definir la función de logaritmo natural por
\[\ln x=∫^x_1\dfrac{1}{t}\,dt. \nonumber \]
Porque\(x>1\), esta es solo el área bajo la curva\(y=\dfrac{1}{t}\) de\(1\) a\(x\). Para\(x<1\), tenemos
\[ ∫^x_1\dfrac{1}{t}\,dt=−∫^1_x\dfrac{1}{t}\,dt, \nonumber \]
por lo que en este caso es el negativo del área bajo la curva de\(x\) a\(1\) (ver la siguiente figura).
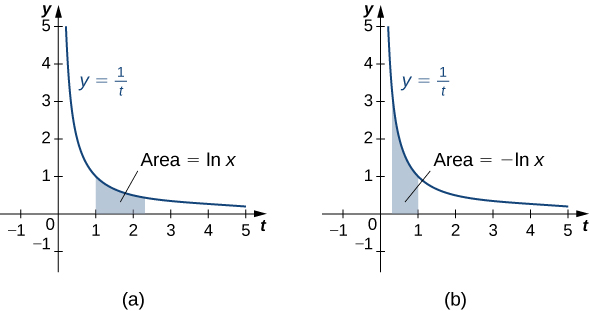
Observe eso\(\ln 1=0\). Además, la función\(y=\dfrac{1}{t}>0\) para\(x>0\). Por lo tanto, por las propiedades de las integrales, es claro que\(\ln x\) va en aumento para\(x>0\).
Propiedades del logaritmo natural
Por la forma en que definimos el logaritmo natural, la siguiente fórmula de diferenciación cae inmediatamente como resultado del Teorema Fundamental del Cálculo.
Para\(x>0\), la derivada del logaritmo natural viene dada por
\[ \dfrac{d}{dx}\Big( \ln x \Big) = \dfrac{1}{x}. \nonumber \]
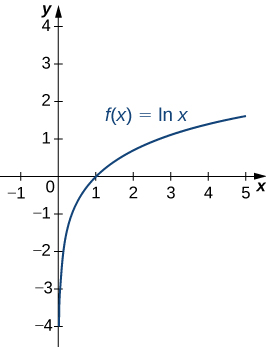
La función\(\ln x\) es diferenciable; por lo tanto, es continua.
Una gráfica de\(\ln x\) se muestra en la Figura. Observe que es continuo en todo su dominio de\((0,∞)\).
Calcular las siguientes derivadas:
- \(\dfrac{d}{dx}\Big(\ln (5x^3−2)\Big)\)
- \(\dfrac{d}{dx}\Big((\ln (3x))^2\Big)\)
Solución
Tenemos que aplicar la regla de la cadena en ambos casos.
- \(\dfrac{d}{dx}\Big(\ln (5x^3−2)\Big)=\dfrac{15x^2}{5x^3−2}\)
- \(\dfrac{d}{dx}\Big((\ln (3x))^2\Big)=\dfrac{2(\ln (3x))⋅3}{3x}=\dfrac{2(\ln (3x))}{x}\)
Calcular las siguientes derivadas:
- \(\dfrac{d}{dx}\Big(\ln (2x^2+x)\Big)\)
- \(\dfrac{d}{dx}\Big((\ln (x^3))^2\Big)\)
- Pista
-
Aplicar la fórmula de diferenciación que se acaba de proporcionar y utilizar la regla de cadena según sea necesario.
- Responder
-
a.\(\dfrac{d}{dx}\Big(\ln (2x^2+x)\Big)=\dfrac{4x+1}{2x^2+x}\)
b.\(\dfrac{d}{dx}\Big((\ln (x^3))^2\Big)=\dfrac{6\ln (x^3)}{x}\)
Tenga en cuenta que si usamos la función de valor absoluto y creamos una nueva función\(\ln |x|\), podemos extender el dominio del logaritmo natural para incluir\(x<0\). Entonces\(\dfrac{d}{dx}\Big( \ln x \Big)=\dfrac{1}{x}\). Esto da lugar a la fórmula de integración familiar.
El logaritmo natural es el antiderivado de la función\(f(u)=\dfrac{1}{u}\):
\[∫\dfrac{1}{u}\,du=\ln |u|+C. \nonumber \]
Calcular la integral\(\displaystyle ∫\dfrac{x}{x^2+4}\,dx.\)
Solución
Usando\(u\) -sustitución, let\(u=x^2+4\). Entonces\(du=2x\,dx\) y tenemos
\(\displaystyle ∫\dfrac{x}{x^2+4}\,dx=\dfrac{1}{2}∫\dfrac{1}{u}\,du=\dfrac{1}{2}\ln |u|+C=\dfrac{1}{2}\ln |x^2+4|+C=\dfrac{1}{2}\ln (x^2+4)+C.\)
Calcular la integral\(\displaystyle ∫\dfrac{x^2}{x^3+6}\,dx.\)
- Pista
-
Aplica la fórmula de integración proporcionada anteriormente y usa u-substitución según sea necesario.
- Responder
-
\(\displaystyle ∫\dfrac{x^2}{x^3+6}\,dx=\dfrac{1}{3}\ln ∣x^3+6∣+C\)
Aunque hemos llamado a nuestra función un “logaritmo”, en realidad no hemos probado que ninguna de las propiedades de logaritmos tenga para esta función. Lo hacemos aquí.
Si\(a,\, b>0\) y\(r\) es un número racional, entonces
- \(\ln 1=0\)
- \(\ln (ab)=\ln a+\ln b\)
- \(\ln \left(\dfrac{a}{b}\right)=\ln a−\ln b\)
- \(\ln \left(a^r\right)=r\ln a\)
i. Por definición,\(\displaystyle \ln 1=∫^1_1\dfrac{1}{t}\,dt=0.\)
ii. Tenemos
\(\displaystyle \ln (ab)=∫^{ab}_1\dfrac{1}{t}\,dt=∫^a_1\dfrac{1}{t}\,dt+∫^{ab}_a\dfrac{1}{t}\,dt.\)
Utilizar\(u-substitution\) en la última integral en esta expresión. Vamos\(u=t/a\). Entonces\(du=(1/a)dt.\) Además, cuando\(t=a,\, u=1\), y cuando\(t=ab,\, u=b.\) Así que obtenemos
\(\displaystyle \ln (ab)=∫^a_1\dfrac{1}{t}\,dt+∫^{ab}_a\dfrac{1}{t}\,dt=∫^a_1\dfrac{1}{t}\,dt+∫^{ab}_1\dfrac{a}{t}⋅\dfrac{1}{a}\,dt=∫^a_1\dfrac{1}{t}\,dt+∫^b_1\dfrac{1}{u}\,du=\ln a+\ln b.\)
iii. Tenga en cuenta que
\(\dfrac{d}{dx}\Big(\ln (x^r)\Big)=\dfrac{rx^{r−1}}{x^r}=\dfrac{r}{x}\).
Además,
\(\dfrac{d}{dx}\Big((r\ln x)\Big)=\dfrac{r}{x}.\)
Dado que las derivadas de estas dos funciones son las mismas, por el Teorema Fundamental del Cálculo, deben diferir por una constante. Así que tenemos
\(\ln (x^r)=r\ln x+C\)
para alguna constante\(C\). Tomando\(x=1\), obtenemos
\(\ln (1^r)=r\ln (1)+C\)
\(0=r(0)+C\)
\(C=0.\)
Así\(\ln (x^r)=r\ln x\) y la prueba está completa. Tenga en cuenta que podemos extender esta propiedad a valores irracionales de\(r\) más adelante en esta sección.
La parte iii. se desprende de las partes ii. y iv. y se le deja la prueba.
□
Utilice las propiedades de logaritmos para simplificar la siguiente expresión en un solo logaritmo:
\( \ln 9−2 \ln 3+\ln \left(\tfrac{1}{3}\right).\)
Solución
Tenemos
\( \ln 9−2 \ln 3+\ln \left(\tfrac{1}{3}\right)=\ln (3^2)−2 \ln 3+\ln (3^{−1})=2\ln 3−2\ln 3−\ln 3=−\ln 3.\)
Utilice las propiedades de logaritmos para simplificar la siguiente expresión en un solo logaritmo:
\( \ln 8−\ln 2−\ln \left(\tfrac{1}{4}\right)\)
- Pista
-
Aplicar las propiedades de logaritmos.
- Responder
-
\(4\ln 2\)
Definición del número e
Ahora que tenemos definido el logaritmo natural, podemos usar esa función para definir el número\(e\).
El número\(e\) se define como el número real de tal manera que
\[\ln e=1\nonumber \]
Para decirlo de otra manera, el área bajo la curva\(y=1/t\) entre\(t=1\) y\(t=e\) es\(1\) (Figura). Te queda la prueba de que tal número existe y es único. (Pista: Utilizar el Teorema del Valor Intermedio para probar la existencia y el hecho de que\(\ln x\) va en aumento para demostrar la singularidad.)
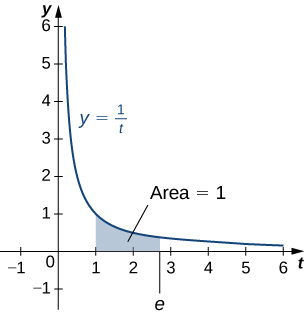
\(e\)Se puede demostrar que el número es irracional, aunque no lo haremos aquí (ver el Proyecto Estudiantil en la Serie Taylor y Maclaurin). Su valor aproximado viene dado por
\( e≈2.71828182846.\)
La función exponencial
Ahora volvemos nuestra atención a la función\(e^x\). Tenga en cuenta que el logaritmo natural es uno a uno y por lo tanto tiene una función inversa. Por ahora, denotamos esta función inversa por\(\exp x\). Entonces,
\[ \exp(\ln x)=x \nonumber \]
para\(x>0\) y
\[ \ln (\exp x)=x \nonumber \]
para todos\(x\).
La siguiente figura muestra las gráficas de\(\exp x\) y\(\ln x\).
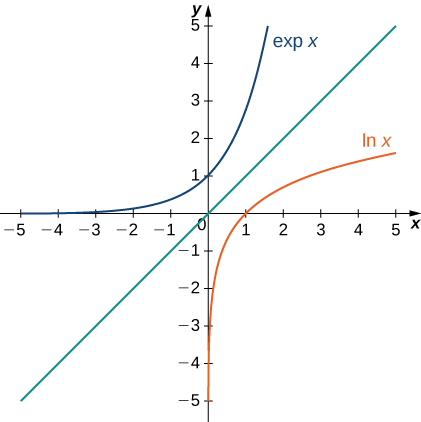
Eso planteamos la hipótesis\(\exp x=e^x\). Para valores racionales de\(x\), esto es fácil de mostrar. Si\(x\) es racional, entonces tenemos\(\ln (e^x)=x\ln e=x\). Así, cuando\(x\) es racional,\(e^x=\exp x\). Para valores irracionales de\(x\), simplemente definimos\(e^x\) como la función inversa de\(\ln x\).
Para cualquier número real\(x\), defina\(y=e^x\) que sea el número para el cual
\[\ln y=\ln (e^x)=x. \nonumber \]
Entonces tenemos\(e^x=\exp x\) para todos\(x\), y así
\(e^{\ln x}=x\)para\(x>0\) y\(\ln (e^x)=x\)
para todos\(x\).
Propiedades de la Función Exponencial
Dado que la función exponencial se definió en términos de una función inversa, y no en términos de un poder de\(e\) debemos verificar que las leyes habituales de los exponentes sostienen para la función\(e^x\).
Si\(p\) y\(q\) son números reales y\(r\) es un número racional, entonces
- \(e^pe^q=e^{p+q}\)
- \(\dfrac{e^p}{e^q}=e^{p−q}\)
- \((e^p)^r=e^{pr}\)
Tenga en cuenta que si\(p\) y\(q\) son racionales, las propiedades se mantienen. Sin embargo, si\(p\) o\(q\) son irracionales, debemos aplicar la definición de función inversa\(e^x\) y verificar las propiedades. Aquí solo se verifica la primera propiedad; las otras dos te quedan a ti. Tenemos
\[ \ln (e^pe^q)=\ln (e^p)+\ln (eq)=p+q=\ln (e^{p+q}).\nonumber \]
Dado que\(\ln x\) es uno a uno, entonces
\[ e^pe^q=e^{p+q}.\nonumber \]
□
Al igual que con la parte iv. de las propiedades del logaritmo, podemos extender la propiedad iii. a valores irracionales de\(r\), y lo hacemos al final de la sección.
También queremos verificar la fórmula de diferenciación para la función\(y=e^x\). Para ello, necesitamos utilizar la diferenciación implícita. Vamos\(y=e^x\). Entonces
\[ \begin{align*} \ln y &=x \\[5pt] \dfrac{d}{dx}\Big(\ln y\Big) &=\dfrac{d}{dx}\Big(x\Big) \\[5pt] \dfrac{1}{y}\dfrac{dy}{dx} &=1 \\[5pt] \dfrac{dy}{dx} &=y. \end{align*}\]
Así, vemos
\[ \dfrac{d}{dx}\Big(e^x\Big)=e^x \nonumber \]
según se desee, lo que conduce inmediatamente a la fórmula de integración
\[ ∫e^x \,dx=e^x+C. \nonumber \]
Aplicamos estas fórmulas en los siguientes ejemplos.
Evaluar los siguientes derivados:
- \(\dfrac{d}{dt}\Big(e^{3t}e^{t^2}\Big)\)
- \(\dfrac{d}{dx}\Big(e^{3x^2}\Big)\)
Solución
Aplicamos la regla de la cadena según sea necesario.
- \(\dfrac{d}{dt}\Big(e^{3t}e^{t^2}\Big)=\dfrac{d}{dt}\Big(e^{3t+t^2}\Big)=e^{3t+t^2}(3+2t)\)
- \(\dfrac{d}{dx}\Big(e^{3x^2}\Big)=e^{3x^2}6x\)
Evaluar los siguientes derivados:
- \(\dfrac{d}{dx}\Big(\dfrac{e^{x^2}}{e^{5x}}\Big)\)
- \(\dfrac{d}{dt}\Big((e^{2t})^3\Big)\)
- Pista
-
Utilice las propiedades de las funciones exponenciales y la regla de cadena según sea necesario.
- Responder
-
a.\(\dfrac{d}{dx}\Big(\dfrac{e^{x^2}}{e^{5x}}\Big)=e^{x^{2−5x}}(2x−5)\)
b.\(\dfrac{d}{dt}\Big((e^{2t})^3\Big)=6e^{6t}\)
Evaluar la siguiente integral:\(\displaystyle ∫2xe^{−x^2}\,dx.\)
Solución
Usando\(u\) -sustitución, let\(u=−x^2\). Entonces\(du=−2x\,dx,\) y tenemos
\(\displaystyle ∫2xe^{−x^2}\,dx=−∫e^u\,du=−e^u+C=−e^{−x^2}+C.\)
Evaluar la siguiente integral:\(\displaystyle ∫\dfrac{4}{e^{3x}}\,dx.\)
- Pista
-
Utilizar las propiedades de las funciones exponenciales y\(u-substitution\) según sea necesario.
- Responder
-
\(\displaystyle ∫\dfrac{4}{e^{3x}}\,dx=−\dfrac{4}{3}e^{−3x}+C\)
Funciones Logarítmicas y Exponenciales Generales
Cerramos esta sección observando las funciones exponenciales y logaritmos con bases distintas a\(e\). Las funciones exponenciales son funciones de la forma\(f(x)=a^x\). Tenga en cuenta que a menos que\(a=e\), todavía no tengamos una definición matemáticamente rigurosa de estas funciones para exponentes irracionales. Rectificemos eso aquí definiendo la función\(f(x)=a^x\) en términos de la función exponencial\(e^x\). Luego examinamos logaritmos con bases distintas a e como funciones inversas de funciones exponenciales.
Para cualquiera\(a>0,\) y para cualquier número real\(x\), defina de la\(y=a^x\) siguiente manera:
\[y=a^x=e^{x \ln a}. \nonumber \]
Ahora\(a^x\) se define rigurosamente para todos los valores de\(x\). Esta definición también nos permite generalizar la propiedad iv. de logaritmos y la propiedad iii. de funciones exponenciales para aplicar tanto a valores racionales como irracionales de\(r\). Es sencillo demostrar que las propiedades de los exponentes se mantienen para las funciones exponenciales generales definidas de esta manera.
Ahora apliquemos esta definición para calcular una fórmula de diferenciación para\(a^x\). Tenemos
\(\dfrac{d}{dx}\Big(a^x\Big)=\dfrac{d}{dx}\Big(e^{x\ln a}\Big)=e^{x\ln a}\ln a=a^x\ln a.\)
La fórmula de integración correspondiente sigue inmediatamente.
Vamos\(a>0.\) Entonces,
\[\dfrac{d}{dx}\Big(a^x\Big)=a^x \ln a \nonumber \]
y
\[∫a^x\,dx=\dfrac{1}{\ln a}a^x+C. \nonumber \]
Si\(a≠1\), entonces la función\(a^x\) es uno a uno y tiene una inversa bien definida. Su inverso se denota por\(\log_a x\). Entonces,
\( y=\log_a x\)si y solo si\(x=a^y.\)
Tenga en cuenta que las funciones generales de logaritmo pueden escribirse en términos del logaritmo natural. Vamos\(y=\log_a x.\) Entonces,\(x=a^y\). Tomando el logaritmo natural de ambos lados de esta segunda ecuación, obtenemos
\ [\ begin {align*}\ ln x &=\ ln (a^y)\\ [5pt]
\ ln x&=y\ ln a\\ [5pt]
y&=\ dfrac {\ ln x} {\ ln a}\\ [5pt]
\ log_a x&=\ dfrac {\ ln x} {\ ln a}. \ end {alinear*}\]
Así, vemos que todas las funciones logarítmicas son múltiplos constantes entre sí. A continuación, utilizamos esta fórmula para encontrar una fórmula de diferenciación para un logaritmo con base\(a\). Nuevamente, vamos\(y=\log_a x\). Entonces,
\ [\ begin {align*}\ dfrac {dy} {dx} &=\ dfrac {d} {dx}\ Grande (\ log_a x\ Grande)\\ [5pt]
&=\ dfrac {d} {dx}\ izquierda (\ dfrac {\ ln x} {\ ln a}\ derecha)\\ [5pt]
& =(\ dfrac {1} {\ ln a})\ dfrac {d} {dx}\ Grande (\ ln x\ Grande)\\ [5pt]
&=\ dfrac {1} {\ ln a} ⋅\ dfrac {1} {x} =\ dfrac {1} {x\ ln a}\ end {align*}\]
Vamos\(a>0.\) Entonces,
\[\dfrac{d}{dx}\Big(\log_a x\Big)=\dfrac{1}{x\ln a}. \nonumber \]
Evaluar los siguientes derivados:
- \(\dfrac{d}{dt}\Big(4^t⋅2^{t^2}\Big)\)
- \(\dfrac{d}{dx}\Big(\log_8(7x^2+4)\Big)\)
Solución: Necesitamos aplicar la regla de la cadena según sea necesario.
- \(\dfrac{d}{dt}\Big(4^t⋅2^{t^2}\Big)=\dfrac{d}{dt}\Big(2^{2t}⋅2^{t^2}\Big)=\dfrac{d}{dt}\Big(2^{2t+t^2}\Big)=2^{2t+t^2}\ln (2)(2+2t)\)
- \(\dfrac{d}{dx}\Big(\log_8(7x^2+4)\Big)=\dfrac{1}{(7x^2+4)(\ln 8)}(14x)\)
Evaluar los siguientes derivados:
- \(\dfrac{d}{dt}\Big(4^{t^4}\Big)\)
- \(\dfrac{d}{dx}\Big(\log_3(\sqrt{x^2+1})\Big)\)
- Pista
-
Utilice las fórmulas y aplique la regla de la cadena según sea necesario.
- Responder
-
a.\(\dfrac{d}{dt}\Big(4^{t^4}\Big)=4^{t^4}(\ln 4)(4t^3)\)
b.\(\dfrac{d}{dx}\Big(\log_3(\sqrt{x^2+1})\Big)=\dfrac{x}{(\ln 3)(x^2+1)}\)
Evaluar la siguiente integral:\(\displaystyle ∫\dfrac{3}{2^{3x}}\,dx.\)
Solución
Usar\(u-substitution\) y dejar\(u=−3x\). Entonces\(du=−3\,dx\) y tenemos
\[ ∫\dfrac{3}{2^{3x}}\,dx=∫3⋅2^{−3x}\,dx=−∫2^u\,du=−\dfrac{1}{\ln 2}2^u+C=−\dfrac{1}{\ln 2}2^{−3x}+C.\nonumber \]
Evaluar la siguiente integral:\(\displaystyle ∫x^2 2^{x^3}\,dx.\)
- Pista
-
Usar las propiedades de las funciones exponenciales y la sustitución en U
- Responder
-
\(\displaystyle ∫x^2 2^{x^3}\,dx=\dfrac{1}{3\ln 2}2^{x^3}+C\)
Conceptos clave
- El tratamiento anterior de logaritmos y funciones exponenciales no definía las funciones de manera precisa y formal. Esta sección desarrolla los conceptos de una manera matemáticamente rigurosa.
- La piedra angular del desarrollo es la definición del logaritmo natural en términos de una integral.
- La función\(e^x\) se define entonces como la inversa del logaritmo natural. Las funciones exponenciales generales se definen en términos de\(e^x\), y las funciones inversas correspondientes son logaritmos generales.
- Las propiedades familiares de logaritmos y exponentes aún se mantienen en este contexto más riguroso.
Ecuaciones Clave
- Función de logaritmo natural
- \(\displaystyle \ln x=∫^x_1\dfrac{1}{t}\,dt\)
- Función exponencial\(y=e^x\)
- \(\ln y=\ln (e^x)=x\)