1.9: Extremos crecientes, decrecientes y locales
- Page ID
- 117192
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Recordemos que la pendiente de una línea es positiva si, y sólo si, la línea se eleva de izquierda a derecha. Es decir, si\(m>0, f(x)=m x+b,\) y\(u<v,\) entonces
\[\begin{aligned} f(v) &=m v+b \\ &=m v-m u+m u+b \\ &=m(v-u)+m u+b \\ &>m u+b \\ &=f(u) . \end{aligned}\] Debemos esperar que se mantenga una sentencia análoga para funciones diferenciables: si\(f\) es diferenciable y\(f^{\prime}(x)>0\) para todos\(x\) en un intervalo\((a, b),\) entonces\(f(v)>f(u)\) para cualquiera\(v>u\) en\((a, b) .\) Este es de hecho el caso, aunque la inferencia requiere establecer una conexión directa entre la pendiente en un punto y la pendiente promedio a lo largo de un intervalo, o, en términos de tasas de cambio, entre la tasa instantánea de cambio en un punto y la tasa promedio de cambio en un intervalo. El teorema del valor medio hace esta conexión.El teorema del valor medio
Recordemos que la propiedad de valor extremo nos dice que una función continua en un intervalo cerrado debe alcanzar tanto un valor mínimo como un valor máximo. Supongamos que\(f\) es continuo en\([a, b],\) diferenciable\(f\) encendido\((a, b),\) y alcanza un valor máximo en\(c\) con\(a<c<b .\) En particular, para cualquier infinitesimal\(d x, f(c) \geq f(c+d x),\) y así, equivalentemente, De\(f(c+d x)-f(c) \leq 0 .\) ello se deduce que si\(d x>0,\)
\[\frac{f(c+d x)-f(c)}{d x} \leq 0 ,\] y si\(d x<0\), \[\frac{f(c+d x)-f(c)}{d x} \geq 0 .\] Dado que ambos valores deben estar infinitesimalmente cercanos al mismo número real, debe darse el caso \[\frac{f(c+d x)-f(c)}{d x} \simeq 0 .\] que Es decir, debemos tener\(f^{\prime}(c)=0 .\) Un resultado similar se mantiene si\(f\) tiene un mínimo en\(c,\) y así tenemos el siguiendo el resultado básico.Teorema\(\PageIndex{1}\)
Si\(f\) es diferenciable\((a, b)\) y alcanza un valor máximo, o mínimo, en\(c,\) ese momento\(f^{\prime}(c)=0\).
Ahora supongamos que\(f\) es continuo en\([a, b],\) diferenciable encendido\((a, b),\) y\(f(a)=f(b) .\) si\(f\) es una función constante, entonces\(f^{\prime}(c)=0\) para todos\(c\) en\((a, b) .\) Si no\(f\) es constante, entonces hay un punto\(c\)\((a, b)\) en el que\(f\) alcanza ya sea una máximo o un valor mínimo, y así\(f^{\prime}(c)=0 .\) En cualquier caso, tenemos el siguiente resultado, conocido como teorema de Rolle.
Teorema\(\PageIndex{2}\)
Si\(f\) es continuo en\([a, b],\) diferenciable encendido\((a, b),\) y\(f(a)=f(b),\) luego hay un número real\(c\) en\((a, b)\) para el cual\(f^{\prime}(c)=0\).
Más generalmente, supongamos que\(f\) es continuo\([a, b]\) y diferenciable en\((a, b) .\)
Let \[g(x)=f(x)-\frac{f(b)-f(a)}{b-a}(x-a)-f(a) .\] Note que\(g(x)\) es la diferencia entre\(f(x)\) y el\(y\) valor correspondiente en la línea que pasa a través\((a, f(a))\) y\((b, f(b)) .\) Por otra parte,\(g\) es continuo en\([a, b],\) diferenciable en\((a, b),\) y\(g(a)=0=g(b) .\) Por lo tanto se aplica el teorema de Rolle a\(g,\) lo que debe existir un punto\(c\) en\((a, b)\) el que\(g^{\prime}(c)=0 .\) Ahora \[g^{\prime}(c)=f^{\prime}(x)-\frac{f(b)-f(a)}{b-a} .\]así que debemos tener
\[0=g^{\prime}(c)=f^{\prime}(c)-\frac{f(b)-f(a)}{b-a} .\] Es decir, \[f^{\prime}(c)=\frac{f(b)-f(a)}{b-a} ,\] que es nuestra conexión deseada entre las tasas de cambio instantáneas y medias, conocida como el teorema del valor medio.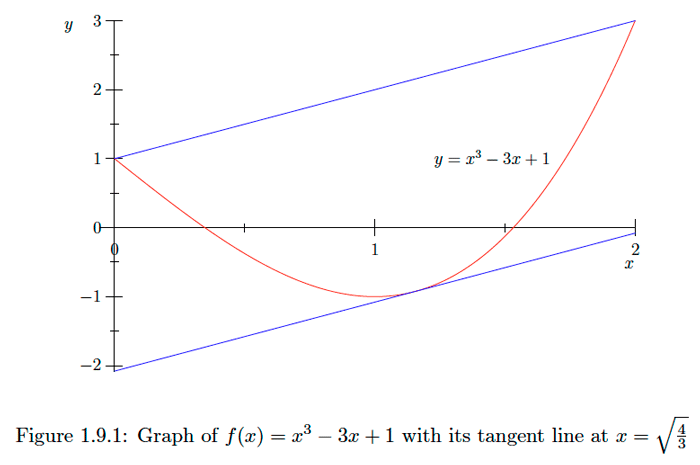
Teorema\(\PageIndex{3}\)
Si\(f\) es continuo\([a, b]\) y diferenciable en\((a, b),\) entonces existe un número real\(c\) en\((a, b)\) el que
\[f^{\prime}(c)=\frac{f(b)-f(a))}{b-a} .\]Ejemplo\(\PageIndex{1}\)
Considera la función\(f(x)=x^{3}-3 x+1\) en el intervalo\([0,2]\). Por el teorema del valor medio, debe existir al menos un punto\(c\) en\([0,2]\) el que
\[f^{\prime}(c)=\frac{f(2)-f(0)}{2-0}=\frac{3-1}{2}=1 .\] Ahora\(f^{\prime}(x)=3 x^{2}-3,\) así\(f^{\prime}(c)=1\) implica\(3 c^{2}-3=1 .\) De ahí\(c=\sqrt{\frac{4}{3}}\). Tenga en cuenta que esto implica que la línea tangente a la gráfica de\(f\) at\(x=\sqrt{\frac{4}{3}}\) es paralela a la línea a través de los puntos finales de la gráfica de es\(f,\) decir, los puntos\((0,1)\) y\((2,3) .\) Ver Figura\(1.9 .1 .\)Funciones crecientes y decrecientes
La discusión anterior nos lleva a la siguiente definición y teorema.
Definición
Decimos que una función\(f\) está aumentando en un intervalo\(I\) si, siempre que\(a<b\) sean puntos en\(I, f(a)<f(b) .\) Similarmente, decimos que\(f\) es decreciente en\(I\) si, siempre que\(a<b\) sean puntos en\(I, f(a)>f(b) .\)
Ahora supongamos que\(f\) es un definido en un intervalo\(I\) y\(f^{\prime}(x)>0\) para cada uno\(x\) en el\(I\) que no es un punto final de\(I\). Entonces dado cualquiera\(a\) y\(b\) en\(I,\) por el teorema del valor medio existe un punto\(c\) entre\(a\) y\(b\) para el cual
\[\frac{f(b)-f(a)}{b-a}=f^{\prime}(c)>0 .\] ya que\(b-a>0,\) esto implica que\(f(b)>f(a) .\) Por lo tanto\(f\) está aumentando en\(I .\) Un argumento similar muestra que\(f\) está disminuyendo en\(I\) si\(f^{\prime}(x)<0\) para cada\(x\) en el\(I\) que no es un punto final de\(I .\)Teorema\(\PageIndex{4}\)
Supongamos que\(f\) se define en un intervalo\(I .\) Si\(f^{\prime}(x)>0\) para cada\(x\) en el\(I\) que no es un punto final de\(I,\) entonces\(f\) está aumentando en\(I .\) Si\(f^{\prime}(x)<0\) para cada\(x\) en el\(I\) que no es un punto final de\(I,\) entonces\(f\) es decreciente en\(I .\)
Ejemplo\(\PageIndex{2}\)
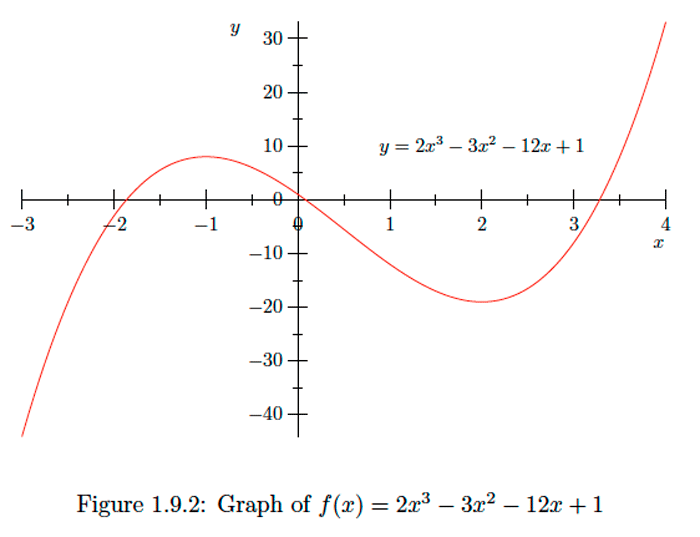
Vamos\(f(x)=2 x^{3}-3 x^{2}-12 x+1 .\) Entonces
\[f^{\prime}(x)=6 x^{2}-6 x-12=6\left(x^{2}-x-2\right)=6(x-2)(x+1) .\] De ahí\(f^{\prime}(x)=0\) cuándo\(x=-1\) y cuándo\(x=2 .\) Ahora\(x-2<0\) por\(x<2\) y\(x-2>0\) por un\(x>2,\) tiempo\(x+1<0\) para\(x<-1\) y\(x+1>0\)\(f^{\prime}(x)>0\) cuándo\(x>-1 .\) Así cuándo\(x<-1<\)\(x>2,\) y\(f^{\prime}(x)<0\) cuándo y\(-1<x<2 .\) cuándo sigue que\(f\) está aumentando en los intervalos\((-\infty,-1)\) y\((2, \infty),\) y disminuyendo en el intervalo\((-1,2) .\) Tenga en cuenta que el teorema solo requiere que sepamos el signo de\(f^{\prime}\) en puntos dentro de un intervalo dado, no en los puntos finales. De ahí que en realidad nos permita hacer la afirmación un poco más fuerte que\(f\) está aumentando en los intervalos\((-\infty,-1]\)\([2, \infty),\) y y disminuyendo en el intervalo\([-1,2] .\) Ya que\(f\) está aumentando en\((-\infty,-1]\) y disminuyendo en\([-1,2],\) el punto\((-1,8)\) debe ser un alto punto en la gráfica de\(f,\) aunque no necesariamente el punto más alto de la gráfica. Decimos que\(f\) tiene un máximo local de 8 a\(x=-1\). De igual manera,\(f\) va disminuyendo\([-1,2]\) y aumentando\([2, \infty),\) y así el punto\((2,-19)\) debe ser un punto bajo en la gráfica de\(f,\) aunque, de nuevo, no necesariamente el punto más bajo de la gráfica. Decimos que\(f\) tiene un mínimo local de\(-19\) al A\(x=2 .\) partir de esta información, podemos comenzar a ver por qué la gráfica de\(f\) miradas como lo hace en la Figura\(1.9 .2 .\)Definición
Decimos\(f\) tiene un marimum local en un punto\(c\) si existe un intervalo\((a, b)\) que contiene\(c\) para el cual\(f(c) \geq f(x)\) para todos\(x\) en\((a, b) .\) Similarmente, decimos que\(f\) tiene un mínimo local en un punto\(c\) si existe un intervalo\((a, b)\) que contiene \(c\)para lo cual\(f(c) \leq f(x)\) para todos\(x\) en\((a, b) .\) Decimos\(f\) tiene un extremo local en\(c\) si\(f\) tiene ya sea un máximo local o un mínimo local en\(c .\)
Ahora podemos replantear el Teorema 1.9 .1 de la siguiente manera.
Teorema\(\PageIndex{5}\)
Si\(f\) es diferenciable en\(c\) y tiene un extremo local en\(c,\) ese entonces\(f^{\prime}(c)=0\).
Como se ilustra en el ejemplo anterior, podemos identificar mínimos locales de una función\(f\) localizando aquellos puntos en los que\(f\) cambia de decreciente a creciente, y máximos locales localizando aquellos puntos en los que\(f\) cambia de aumentar a disminuir.
Ejemplo\(\PageIndex{3}\)
Que\(f(x)=x+2 \sin (x) .\) Entonces\(f^{\prime}(x)=1+2 \cos (x),\) y así\(f^{\prime}(x)<0\) cuando, y sólo cuando,
\[\cos (x)<-\frac{1}{2} .\] Para\(0 \leq x \leq 2 \pi,\) esto ocurre cuando, y solo cuando, \[\frac{2 \pi}{3}<x<\frac{4 \pi}{3} .\] ya que la función coseno tiene punto\(2 \pi,\) si sigue que\(f^{\prime}(x)<0\) cuando, y solo cuando,\(x\) está en un intervalo de la forma \[\left(\frac{2 \pi}{3}+2 \pi n, \frac{4 \pi}{3}+2 \pi n\right)\] para\(n=0, \pm 1, \pm 2, \ldots\) Por lo tanto\(f\) es decreciente en estos intervalos y aumento en intervalos de la forma \[\left(-\frac{2 \pi}{3}+2 \pi n, \frac{2 \pi}{3}+2 \pi n\right) ,\]\(n=0, \pm 1, \pm 2, \ldots\)Ahora se deduce que\(f\) tiene un máximo local en cada punto de la forma
\[x=\frac{2 \pi}{3}+2 \pi n\] y un mínimo local en cada punto del formulario A \[x=\frac{4 \pi}{3}+2 \pi n .\] partir de esta información, podemos comenzar a ver por qué la gráfica de\(f\) miradas como lo hace en la Figura\(1.9 .3 .\)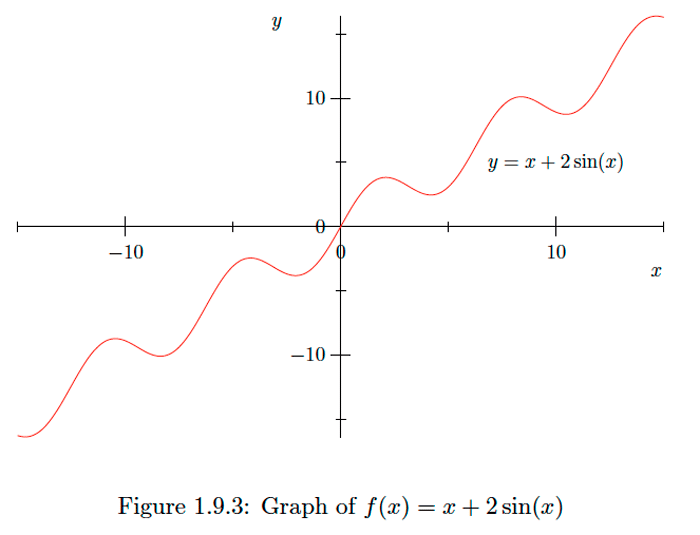
Ejercicio\(\PageIndex{1}\)
Encuentra los intervalos donde\(f(x)=x^{3}-6 x\) está aumentando y los intervalos donde\(f\) está disminuyendo. Utilice esta información para identificar cualquier máximo local o mínimo local de\(f .\)
- Contestar
-
\(f\)está aumentando\((-\infty,-\sqrt{2})\) y\([\sqrt{2}, \infty],\) disminuyendo en\([-\sqrt{2}, \sqrt{2}]\);\(f\) tiene un máximo local de\(4 \sqrt{2}\) at\(x=-\sqrt{2}\) y un mínimo local de\(-4 \sqrt{2}\) at\(x=\sqrt{2} .\)
Ejercicio\(\PageIndex{2}\)
Encuentra los intervalos donde\(f(x)=5 x^{3}-3 x^{5}\) está aumentando y los intervalos donde\(f\) está disminuyendo. Utilice esta información para identificar cualquier máximo local o mínimo local de\(f .\)
- Contestar
-
\(f\)está aumentando una\([-1,0]\) y otra vez\([0,1]\) (o, simplemente,\([-1,1] ; f\) está disminuyendo una\((-\infty,-1]\) y otra vez\([1, \infty) ; f\) tiene un máximo local de 2 a\(x=1\) y un mínimo local de\(-2\) en\(x=-1 .\)
Ejercicio\(\PageIndex{3}\)
Encuentra los intervalos donde\(f(x)=x+\sin (x)\) está aumentando y los intervalos donde\(f\) está disminuyendo. Utilice esta información para identificar cualquier máximo local o mínimo local\(f .\)
- Contestar
-
\(f\)está aumentando en todos los intervalos de la forma\([-n \pi, n \pi],\) donde\(n=1,2, \dots ;\)\(f \text { has no local maximums or minimums (indeed, } f \text { is increasing on }(-\infty, \infty))\).


