3.3: Operaciones en Sets

Hay varias formas importantes en las que se puede hacer un nuevo conjunto a partir de conjuntos que ya tienes. Cualquier método para hacer esto se llama operación de conjunto.

3.3A. Unión e Intersección.

Dos de las operaciones más básicas son la unión y la intersección. Hablemos primero de ellos en términos informales. Supongamos:

• Alice y Bob van a tener una fiesta, y hay que decidir a quién se le debe invitar,
• Alice hizo una lista de todas las personas a las que le gustaría invitar, y
• Bob hizo una lista de todas las personas a las que le gustaría invitar.

Aquí están dos de las muchas decisiones posibles que podrían tomar.

1. Una solución sería invitar a todos los que están en cualquiera de las listas. Es decir, podrían comenzar su lista de invitaciones anotando todos los nombres en la lista de Alice, y luego agregar todos los nombres de la lista de Bob (o, más precisamente, los nombres de la lista de Bob que no están ya incluidos en la lista de Alice). Esta es la unión de las listas.
2. Una solución mucho más conservadora sería invitar solo a las personas que aparecen en ambas listas. Es decir, podrían pasar por la lista de Alice, y tachar a todos los que no aparecen en la lista de Bob. (Obtendrían el mismo resultado revisando la lista de Bob, y tachando a todos los que no aparecen en la lista de Alice). Esta es la intersección de las listas.

Definición\(3.3.1\).

Supongamos\(A\) y\(B\) son conjuntos.

1. La unión de\(A\) y\(B\) es el conjunto\[A \cup B=\{x \mid x \in A \text { or } x \in B\} .\]
2. La intersección de\(A\) y\(B\) es el conjunto\[A \cap B = \{A \cap B=\{x \mid x \in A \text { and } x \in B\} .\]

OBSERVACIÓN\(3.3.2\).

Al dibujar los conjuntos\(A\) y\(B\) como círculos superpuestos, la unión y la intersección se pueden representar de la siguiente manera:

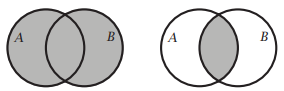
\(A \cup B\)está sombreado\(A \cap B\) está sombreado

Fotos como estas se llaman diagramas de Venn.

OBSERVACIÓN\(3.3.3\).

1. En inglés ordinario, la palabra “intersección” se refiere a donde se encuentran dos cosas. Por ejemplo, la intersección de dos calles es donde se juntan las dos calles. Podemos pensar en esta zona como parte de ambas calles, por lo que esto es consistente con la forma en que se usa el término en matemáticas.
2. En inglés ordinario, la palabra “union” se refiere a unir las cosas. Por ejemplo, un matrimonio es la unión de dos personas —une a las dos personas en una pareja soltera casada. Esto es consistente con la forma en que se usa el término en matemáticas — podríamos formar la unión de la lista de Alice y la lista de Bob pegando la lista de Bob al final de la lista de Alice.

Ejemplo\(3.3.4\).

1. \(\{1,3,5,7,9\} \cup \{1,4,7,10\} = \{1,3,4,5,7,9,10\}\)
2. \(\{1,3,5,7,9\} \cap \{1,4,7,10\} = \{1,7\}\)

Solución

Agrega texto aquí.

Ejercicio\(\PageIndex{1}\)

Especifique cada conjunto enumerando sus elementos. (No es necesario que muestres tu trabajo. )

1. \(\{1,2,3,4\} \cup\{3,4,5,6,7\}=\)
2. \(\{1,2,3,4\} \cap\{3,4,5,6,7\}=\)
3. \(\{\mathrm{p}, \mathrm{r}, \mathrm{o}, \mathrm{n}, \mathrm{g}\} \cap\{\mathrm{h}, \mathrm{o}, \mathrm{r}, \mathrm{n}, \mathrm{s}\}=\)
4. \(\{\mathrm{p}, \mathrm{r}, \mathrm{o}, \mathrm{n}, \mathrm{g}\} \cup\{\mathrm{h}, \mathrm{o}, \mathrm{r}, \mathrm{n}, \mathrm{s}\}=\)
5. \((\{1,3,5\} \cup\{2,3,4\}) \cap\{2,4,6\}=\)
6. \((\{1,3,5\} \cap\{2,3,4\}) \cup\{2,4,6\}=\)

Ejercicio\(3.3.6\).

1. Asumir\(A\) y\(B\) son conjuntos. Demostrar que si\(c \in A \cap B\), entonces\(c \in A\).
2. Supongamos\(X\)\(Y\),, y\(Z\) son conjuntos. Demostrar que si\(r \in (X \cap Y) \cup (X \cap Z)\), entonces\(r \in X\).

OBSERVACIÓN\(3.3.7\).

1. No es difícil verlo\(\cup\) y\(\cap\) son conmutativos. Es decir, para todos los conjuntos\(A\) y\(B\), tenemos\[A \cup B=B \cup A \quad \text { and } \quad A \cap B=B \cap A\]

2. Tampoco es difícil verlo\(\cup\) y\(\cap\) son asociativos. Es decir, para todos los conjuntos\(A\),\(B\), y\(C\), tenemos\[(A \cup B) \cup C=A \cup(B \cup C) \quad \text { and } \quad(A \cap B) \cap C=A \cap(B \cap C)\]
   Así que no hay necesidad de paréntesis a la hora de escribir\(A \cup B \cup C\) o\(A \cap B \cap C\). (Sin embargo, necesitas paréntesis al escribir algo así como\(A \cup (B \cap C)\) o\((A \cup B) \cap C\), que usa ambos\(\cup\) y\(\cap\).)

Ejemplo\(3.3.8\).

Un diagrama de Venn puede incluir más de dos conjuntos. Por ejemplo, aquí están los diagramas de Venn de\(A \cap B \cap C\) y\(A \cap (B \cup C)\).

\(A \cap B \cap C\)está sombreado\(A \cap (B \cup C)\) está sombreado

Solución

Agrega texto aquí.

Ejercicio\(3.3.9\).

Dibuja un diagrama de Venn de cada conjunto. (No es necesario que muestres tu trabajo. )

1. \(A \cup B \cup C\)
2. \(A \cup(B \cap C)\)
3. \((A \cup B) \cap C\)
4. \((A \cap C) \cup(B \cap C)\)

Contestar

Agrega textos aquí. No elimine primero este texto.

3.3B. Establecer Diferencia y Complemento

La “diferencia establecida” es otra operación fundamental.

Ejemplo\(3.3.10\).

Si hay una lista de personas a las que Alice quisiera invitar al partido, y también una lista de personas a las que Bob se niega a permitir que acudan al partido (la “lista de veto”), entonces sería razonable invitar a las personas que están en la lista de Alice, pero no en la lista de veto. Es decir, podrían comenzar con la lista de Alice, y eliminar todos los nombres que están en la lista de Bob. Esta es la diferencia establecida de la lista de Alice y la lista de Bob.

Definición\(3.3.11\).

Supongamos\(A\) y\(B\) son conjuntos.

1. La diferencia de conjunto de\(A\) y\(B\) es el conjunto\[A \backslash B=\{x \in A \mid x \notin B\}=\{x \mid(x \in A) \&(x \notin B)\} .\]

2. El complemento de\(B\) es el conjunto\[\bar{B}=\mathcal{U} \backslash B=\{x \mid x \notin B\}\]
   donde\(\mathcal{U}\) está el conjunto universal, como siempre.

Otra Notación.

Algunos autores escriben\(A - B\), en lugar de\(A \backslash B\). Además, algunos autores escriben\(B^{c}\), en lugar de\(\bar{B}\)

OBSERVACIÓN\(3.3.12\).

Aquí están los diagramas de Venn.

\(A \backslash B\)está sombreado\(B \backslash A\) está sombreado

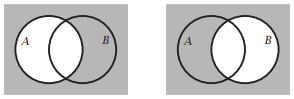
\(\bar{A}\)está sombreado\(\bar{B}\) está sombreado

Ejemplo\(3.3.13\).

Supongamos que\(\mathcal{U}=\mathrm{PEOPLE}\) es el conjunto de todas las personas.

1. \(\overline{\text { CHILDREN }}=\text { ADULTS }\), porque los adultos son las personas que no son niños.
2. \(\text { FEMALES } \backslash \text { CHILDREN }\)es el conjunto de todas las mujeres adultas.

Ejercicio\(3.3.14\).

Asumir\(\mathcal{U}=\{1,2,3, \ldots, 10\}\). Especifique cada conjunto enumerando sus elementos. (No es necesario que muestres tu trabajo. )

1. \(\{1,3,5,7,9\} \backslash\{4,5,6,7\}=\)
2. \(\{4,5,6,7\} \backslash\{1,3,5,7,9\}=\)
3. \(\overline{\{1,3,5,7,9\}}=\)
4. \(\overline{\{4,5,6,7\}}=\)

Ejercicio\(3.3.15\).

Dibuja un diagrama de Venn de cada conjunto. (No es necesario que muestres tu trabajo. )

1. \(\overline{A \cup B}\)
2. \(\overline{A \cap B}\)
3. \((A \vee B) \backslash(A \vee C)\)
4. \(A \backslash(B \backslash C)\)
5. \((A \cup B) \backslash C\)

Ejemplo\(3.3.16\).

Supongamos\(A\) y\(B\) son conjuntos. Demuéstralo si\(c \in \overline{A \cup B}\), entonces\(c \in \bar{A} \cap \bar{B}\).

Solución

Asumir\(c \in \overline{A \cup B}\). Por definición del complemento, esto significa\(c \notin A \cup B\). En otras palabras, eso no es cierto\(c \in A \cup B\). De la definición de\(A \cup B\), concluimos que\[\text { it is not true that either } c \in A \text { or } c \in B \text {. }\]
Por las reglas de negación, esto significa\(c \notin A\) y\(c \notin B\). Ahora:

• ya que\(c \notin A\), tenemos\(c \in \bar{A},\), y
• ya que\(c \notin B\), tenemos\(c \in \bar{B}\).

Por lo tanto, sabemos\(c \in \bar{A}\) y\(c \in \bar{B}\), entonces\(c \in \bar{A} \cap \bar{B}\).

Ejercicio\(3.3.17\).

Supongamos\(A\) y\(B\) son conjuntos. Demuéstralo si\(c \in \bar{A} \cap \bar{B}\), entonces\(c \in \overline{A \cup B}\).

3.3C. Conjuntos disjuntos

Definición\(3.3.18\).

Dos conjuntos\(A\) y\(B\) se dice que son disjuntos si su intersección está vacía (es decir,\(A \cap B=\varnothing\)). En otras palabras, no tienen elementos en común:\ [A\ text {y} B\ text {son disjuntos}\ Leftrightarrow\ begin {reunió}
\ text {no existe un} x,\\
\ texto {tal que} ((x\ in A)\ & (x\ in B)).
\ end {reunidos}\] También
podemos decir que\(A\) es disjunta de B.

Ejemplo\(3.3.19\).

1. Los conjuntos\(\{1,3,5\}\) y\(\{2,4,6\}\) son disjuntos, porque no tienen elementos en común.
2. Los conjuntos\(\{1,3,5\}\) y no\(\{2,3,4\}\) son disjuntos, porque\(3\) está en su intersección.
3. El siguiente diagrama de Venn ilustra dos conjuntos disjuntos\(A\) y\(B\) (no se superponen):

\(A\)y\(B\) son disjuntas

OBSERVACIÓN\(3.3.20\).

Señalemos algunos hechos bien conocidos que se probarán formalmente en el Capítulo\(9\).

1. Si\(A\) y\(B\) son dos conjuntos disjuntos, entonces\(\#(A \cup B)=\# A+\# B\).
2. La situación es similar aunque haya más de\(2\) conjuntos: Supongamos que\(A_1,A_2,\ldots,A_n\) son conjuntos par-disjuntos. (Esto significa que\(A_i\) es disjunta de\(A_j\) cuando sea\(i \neq j\).) Entonces\[\#\left(A_{1} \cup A_{2} \cup \cdots \cup A_{n}\right)=\# A_{1}+\# A_{2}+\cdots+\# A_{n} .\]
3. Si\(A\) y\(B\) son dos conjuntos finitos que no son disjuntos, entonces\(\#(A \cup B)<\# A+\# B\).

3.3D. El Power Set.

Ejemplo\(3.3.21\).

No es difícil enumerar todos los subconjuntos de\(\{a,b,c\}\). Una forma de hacerlo es considerar el posible número de elementos en el subconjunto:

0. Un subconjunto con\(0\) elementos no tiene ningún elemento. Debe ser el conjunto vacío\(\varnothing\).
1. Considera un subconjunto con\(1\) elemento. Ese elemento debe ser uno de los elementos de\(\{a,b,c\}\). Es decir, el elemento del conjunto debe ser\(a\),\(b\), o\(c\). Entonces los subconjuntos de 1 elemento son\(\{a\}\),\(\{b\}\), y\(\{c\}\).
2. Considera los subconjuntos con\(2\) elementos.
   • Si\(a\) es uno de los elementos en el subconjunto, entonces el otro elemento debe ser cualquiera\(b\) o\(c\).
   • Si no\(a\) está en el subconjunto, entonces el subconjunto debe contener ambos\(b\) y\(c\).

   Por lo tanto, los subconjuntos\(2\) -element son\(\{a,b\}\),\(\{a,c\}\), y\(\{b,c\}\).

3. Un subconjunto con\(3\) elementos debe tener todos los elementos de\(\{a,b,c\}\), por lo que el subconjunto debe ser\(\{a,b,c\}\).
4. Porque solo\(\{a,b,c\}\) tiene\(3\) elementos, sabemos que ningún subconjunto puede tener más que\(3\) elementos.

Así, los subconjuntos de\(\{a,b,c\}\) son\[\varnothing,\{a\},\{b\},\{c\},\{a, b\},\{a, c\},\{b, c\},\{a, b, c\} .\]
Contándolos, vemos que hay exactamente\(8\) subconjuntos.

OBSERVACIÓN\(3.3.22\).

En general, se puede mostrar que cualquier conjunto con\(n\) elementos tiene exactamente\(2^{n}\) subconjuntos. En el ejemplo anterior, tenemos\(n = 3\), y el número de subconjuntos es\(2^{3} = 8\).

Ejercicio\(3.3.23\).

(No es necesario que muestres tu trabajo. )

1. Enumere los subconjuntos de\(\{a\}\).
2. Enumere los subconjuntos de\(\{a,b\}\).
3. Enumere los subconjuntos de\(\{a,b,c,d\}\).
4. Enumere los subconjuntos de\(\varnothing\).

Podemos hacer un conjunto poniendo llaves de conjunto en los extremos de la lista anterior de subconjuntos de\(\{a,b,c\}\):\[\{\varnothing,\{a\},\{b\},\{c\},\{b, c\},\{a, c\},\{a, b\},\{a, b, c\}\} .\]
En general, el conjunto de todos los subconjuntos de un conjunto se llama su conjunto de potencia:

Definición\(3.3.24\).

Supongamos que\(A\) es un conjunto. El conjunto de potencia de\(A\) es el conjunto de todos los subconjuntos de\(A\). Se denota\(\mathcal{P}(A)\). Esto significa\[\mathcal{P}(A)=\{B \mid B \subset A\} .\]

OBSERVACIÓN\(3.3.25\).

De Remark\(3.3.22\)., vemos que si\(\#A = n\), entonces\(\# \mathcal{P}(A)=2^{n}\). Esta fórmula que implica “dos a la -\(n\) ésima potencia” puede considerarse una justificación para llamar\(\mathcal{P}(A)\) al conjunto de potencia.

Ejercicio\(3.3.26\).

1. Describa cada uno de los siguientes conjuntos enumerando sus elementos.
   (No es necesario que muestres tu trabajo. )
   1. \(\mathcal{P}(\varnothing)\)
   2. \(\mathcal{P}(\{\mathrm{a}\})\)
   3. \(\mathcal{P}(\{\mathrm{a}, \mathrm{b}\})\)
   4. \(\mathcal{P}(\{\mathrm{a}, \mathrm{b}, \mathrm{c}\})\)
   5. \(\mathcal{P}(\{\mathrm{a}, \mathrm{b}, \mathrm{c}, \mathrm{d}\})\)
2. ¿Cuáles de los siguientes son elementos de\(\mathcal{P}(\{\mathrm{a}, \mathrm{b}, \mathrm{c}, \mathrm{d}\})\)?
   (No es necesario que muestres tu trabajo. )
   1. \(a\)
   2. \(\{\mathrm{a}\}\)
   3. \(\{a, b\}\)
   4. \(\{\mathrm{a}, \mathrm{c}\}\)
3. Supongamos que\(A\) es un conjunto.
   1. ¿Es\(\varnothing \in \mathcal{P}(A)\)? ¿Por qué?
   2. ¿Es\(A \in \mathcal{P}(A)\)? ¿Por qué?
4. ¿Existe un conjunto\(A\), tal que\(\mathcal{P}(A)=\varnothing\)?
5. Dejar\[V_{0}=\varnothing, \quad V_{1}=\mathcal{P}\left(V_{0}\right), \quad V_{2}=\mathcal{P}\left(V_{1}\right)=\mathcal{P}\left(\mathcal{P}\left(V_{0}\right)\right), \quad \text { and so forth. }\]
   En general,\(V_{n}=\mathcal{P}\left(V_{n-1}\right)\) cuando sea\(n > 0\).
   1. ¿Cuáles son las cardinalidades de\(V_{0}\)\(V_{1}\),\(V_{2}\),\(V_{3}\),\(V_{4}\), y\(V_{5}\)?
   2. Describir\(V_{0}\)\(V_{1}\),\(V_{2}\),, y\(V_{3}\) enumerando sus elementos.
   3. (más difícil) Describa\(V_{4}\) enumerando sus elementos.
   4. ¿Es razonable pedirle a alguien que enumere los elementos de\(V_{5}\)? ¿Por qué?