6.2: Introducción informal a las funciones
- Page ID
- 116534
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
Has visto muchos ejemplos de funciones en tus clases anteriores de matemáticas. La mayoría de estos probablemente fueron dados por fórmulas (como\(f(x) = x^{3}\)), pero las funciones también se pueden dar de otras maneras. La propiedad clave de una función es que acepta entradas y proporciona un valor de salida correspondiente para cada entrada posible.
Para la función\(f(x) = x^{3}\), la entrada\(x\) puede ser cualquier número real. Al enchufar un valor\(x\) a la fórmula se obtiene un valor de salida, que también es un número real. Por ejemplo, al usar\(x = 2\) como entrada se obtiene el valor de salida\(f(2) = 2^{3} = 8\).
Supongamos que\(f\) es cualquier función.
- El conjunto de entradas permitidas de\(f\) se llama el dominio de\(f\).
- Si\(A\) es el dominio de\(f\), y\(B\) es cualquier conjunto que contenga todas las salidas posibles de\(f\), entonces decimos que\(f\) es una función de\(A\) a\(B\). En el caso de la función\(f(x) = x^{3}\), podemos tomar\(A\) y\(B\) ser ambos el conjunto de números reales; así,\(f\) es una función de\(\mathbb{R} to \mathbb{R}\).
\(g(x) = 1/x\)no es una función de\(\mathbb{R}\) a\(\mathbb{R}\). Esto se debe a que 0 es un elemento de\(\mathbb{R}\), pero la fórmula no define un valor para\(g(0)\). Así, 0 no puede estar en el dominio de\(g\). Para corregir este problema, se podría decir que\(g\) es una función desde el conjunto\(\{x \in \mathbb{R} \mid x \neq 0\}\) de números reales distintos de cero, hasta\(\mathbb{R}\).
Intuitivamente, se\(B\) puede pensar que una función de\(A\) a es cualquier proceso que acepte entradas del conjunto\(A\), y asigne un elemento del conjunto\(B\) a cada una de estas entradas. El proceso no necesita estar dado por una fórmula. En efecto, la mayoría de las funciones que surgen en la ciencia o en la vida cotidiana no vienen dadas por ninguna fórmula.
- Cada punto de la superficie de la tierra tiene una temperatura particular en este momento, y la temperatura (en grados centígrados) es un número real. Así, la temperatura define una función\(\text {temp}\) desde la superficie de la tierra hasta\(\mathbb{R}\):\(\text {temp} (x)\) es la temperatura en el punto\(x\).
- Los artículos en una tienda de abarrotes tienen cada uno un precio particular, que es un cierto número de centavos, por lo que se\(\text {price}\) puede considerar como una función desde el conjunto de artículos a la venta hasta el conjunto\(\mathbb{N}\) de todos los números naturales:\(\text {price}(x)\) es el precio del artículo\(x\) (en centavos).
- Si dejamos\(\text {People}\) ser el conjunto de todas las personas (vivas o muertas), entonces\(\text {mother}\) es una función de\(\text {People}\) a\(\text {People}\). Por ejemplo,\[\text { mother(Prince Charles) }=\text { Queen Elizabeth. }\]
(Para evitar ambigüedades, tal vez deberíamos aclarar que, por “madre”, queremos decir “madre biológica”). - En contraste, no\(\text {grandmother}\) es una función de\(\text {People}\) a\(\text {People}\). Esto se debe a que la gente no solo tiene una abuela, sino dos (una abuela materna y una abuela paterna). Por ejemplo, si decimos que el príncipe Carlos escribió un poema para su abuela, no sabemos si escribió el poema para la madre de la reina Isabel, o para su otra abuela. Nunca se permite que una función tenga tal ambigüedad. (En términos técnicos,\(\text {grandmother}\) es una “relación”, no una función. Esto se explicará en la Sección\(7.1\).)
Las funciones suelen ser dadas por una tabla de valores.
La lista de precios en una tienda es un ejemplo de esto:

En este ejemplo:
- El dominio del precio es\(\text { \{apple, banana, cherry, donut, egg }\}\).
- \(\text { price(banana) }=83\).
- \(\text { price(guava) }\)no existe, porque no\(\text {guava}\) está en el dominio de la función.
En lugar de hacer una tabla, los matemáticos prefieren representar cada fila de la tabla por un par ordenado. Por ejemplo, la primera fila de la tabla es\(\text {apple } \mid 65\). Esto tiene a\(\text {apple}\) la izquierda y 65 a la derecha, por lo que lo representamos por el par ordenado\((\text {apple}, 65)\), que tiene\(\text {apple}\) a la izquierda y 65 a la derecha. La segunda fila está representada por\((\text {banana}, 83)\). Continuando de esta manera arroja un total de 5 pares ordenados (uno por cada fila). Para mantenerlos reunidos, un matemático los pone en un conjunto. Así, en lugar de escribir una tabla, un matemático representaría esta función como:\[\{(\text { apple, } 65),(\text { banana }, 83),(\text { cherry, } 7),(\text { donut, } 99),(\text { egg, } 155)\} .\]
El conjunto de pares ordenados contiene exactamente la misma información que una tabla de valores, pero el conjunto es una forma más conveniente para manipulaciones matemáticas.
A la derecha hay una función\(f\) dada por una tabla de valores. (No es necesario que muestres tu trabajo en ninguna parte de este problema. )
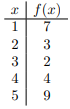
- ¿De qué es el dominio\(f\)?
- ¿Qué es\(f(3)\)?
- Representar\(f\) como un conjunto de pares ordenados.
- Encuentra una fórmula para representar\(f\).
[Pista: Hay una fórmula de la forma\(f(x) = ax^{2} + bx + c\).]
No todas las tablas de valores representan una función. Por ejemplo, supongamos que tenemos la siguiente lista de precios, que es un ligero cambio de Ejemplo\(6.2.5\):

Aquí hay un problema, porque hay dos posibles precios para un plátano, dependiendo de qué línea de la mesa se mire. (Entonces podrías recoger un plátano, esperando pagar 83 centavos, y terminar haciendo que el cajero te cobre $1.55.) Esto no está permitido en una función: cada entrada debe tener exactamente una salida, no un número de salidas posibles diferentes. Por lo tanto, si una tabla representa una función, y un elemento aparece en el lado izquierdo de más de una fila, entonces todas esas filas deben tener la misma salida listada en el lado derecho.
Una tabla de 2 columnas representa una función de\(A\) a\(B\) si y solo si:
- cada valor que aparece en la columna izquierda de la tabla es un elemento de\(A\),
- cada valor que aparece en la columna derecha de la tabla es un elemento de\(B\),
- cada elemento de\(A\) aparece en el lado izquierdo de la mesa, y
- no hay dos filas de la mesa que tengan el mismo lado izquierdo, sino diferentes lados derechos.
¿Cuáles de las siguientes son funciones de\(\{1, 2, 3\}\) a\(\{\text {w, h, o}\}\)? (Si no es tal función, entonces explique por qué no.)
- \(\{(1, \mathrm{w}),(1, \mathrm{~h}),(1, \mathrm{o})\}\)
- \(\{(1, \mathrm{~h}),(2, \mathrm{~h}),(3, \mathrm{~h})\}\)
- \(\{(1, \mathrm{~h}),(2, \mathrm{o}),(3, \mathrm{w})\}\)
- \(\{(\mathrm{w}, 1),(\mathrm{h}, 2),(\mathrm{o},3)\}\)
Solución
- Esto no es una función. Ya que\((1, \mathrm{w})\)\((1, \mathrm{~h})\),, y\((1,\mathrm{o})\) están todos en el conjunto, hay tres elementos diferentes\(b\) (no un único\(b\)), tal que\((1, b)\) está en el conjunto.
- Esta es tal función.
- Esta es tal función.
- Esta no es tal función, porque, para el elemento\((\mathrm{w}, 1)\) del conjunto, no existen elementos\(a\) de\(\{1, 2, 3\}\) y\(b\) de\(\{\mathrm{w}, \mathrm{h}, \mathrm{o}\}\), tal que\((\mathrm{w}, 1)=(a, b)\). (En cambio, tendríamos que tomar\(\{\mathrm{w}, \mathrm{h}, \mathrm{o}\}\) y\(a\)\(b\) entrar\(\{1, 2, 3\}\), lo que está al revés de lo que se requiere. De hecho,\(f\) es una función de\(\{\mathrm{w}, \mathrm{h}, \mathrm{o}\}\) a\(\{1, 2, 3\}\), no de\(\{1, 2, 3\}\) a\(\{\mathrm{w}, \mathrm{h}, \mathrm{o}\}\).)
Let
- \(A=\{\mathrm{a}, \mathrm{b}, \mathrm{c}, \mathrm{d}, \mathrm{e}\}\), y
- \(B=\{1,3,5,7,9,11\}\).
¿Cuál de los siguientes conjuntos de pares ordenados son funciones de\(A\) a\(B\)? (Para los que no lo son, explique por qué.)
- \(\{(\mathrm{a}, 1),(\mathrm{b}, 3),(\mathrm{c}, 5),(\mathrm{d}, 7),(\mathrm{e}, 9)\}\)
- \(\{(\mathrm{a}, 1),(\mathrm{b}, 2),(\mathrm{c}, 3),(\mathrm{d}, 4),(\mathrm{e}, 5)\}\)
- \(\{(\mathrm{a}, 1),(\mathrm{b}, 3),(\mathrm{c}, 5),(\mathrm{d}, 3),(\mathrm{e}, 1)\}\)
- \(\{(\mathrm{a}, 1),(\mathrm{b}, 3),(\mathrm{c}, 5),(\mathrm{d}, 7),(\mathrm{e}, 9),(\mathrm{a}, 11)\}\)
- \(\{(\mathrm{a}, 1),(\mathrm{b}, 3),(\mathrm{c}, 5),(\mathrm{e}, 7)\}\)
- \(\{(\mathrm{a}, 1),(\mathrm{b}, 1),(\mathrm{c}, 1),(\mathrm{d}, 1),(\mathrm{e}, 1)\}\)
- \(\{(\mathrm{a}, \mathrm{a}),(\mathrm{b}, \mathrm{a}),(\mathrm{c}, \mathrm{a}),(\mathrm{d}, \mathrm{a}),(\mathrm{e}, \mathrm{a})\}\)
- \(\{(\mathrm{a}, 1),(\mathrm{b}, 3),(\mathrm{c}, 5),(\mathrm{d}, 5),(\mathrm{e}, 3),(\mathrm{a}, 1)\}\)
- \(\{(1, \mathrm{a}),(3, \mathrm{a}),(5, \mathrm{a}),(7, \mathrm{a}),(9, \mathrm{a}),(11, \mathrm{a})\}\)
- \(\{(\mathrm{c}, 1),(\mathrm{b}, 3),(\mathrm{e}, 5),(\mathrm{a}, 7),(\mathrm{d}, 9)\}\)
A veces es útil representar una función\(f: A \rightarrow B\) dibujando un diagrama de flechas:
- se dibuja un punto para cada elemento de\(A\) y cada elemento de\(B\), y
- se dibuja una flecha de\(a\) a\(f(a)\), para cada uno\(a \in A\).
Por ejemplo, supongamos
- \(A=\{\mathrm{a}, \mathrm{b}, \mathrm{c}, \mathrm{d}, \mathrm{e}\}\),
- \(B=\{1,2,3,4\}\), y
- \(f=\{(\mathrm{a}, 1),(\mathrm{b}, 3),(\mathrm{c}, 4),(\mathrm{d}, 4),(\mathrm{e}, 3)\}\).
Entonces la imagen a la derecha es un diagrama de flechas de\(f\).

Observe que:
- Exactamente hay una flecha saliendo de cada elemento de\(A\). Esto es cierto para el diagrama de flechas de cualquier función.
- Puede haber cualquier número de flechas entrando en cada elemento de\(B\) (quizás ninguna, quizás una, o quizás más de una).


