6.4: Funciones uno a uno

Comenzamos esta sección con un ejemplo.

Ejemplo\(6.4.1\).

1. Supongamos que el inspector Thinkright conoce dos hechos:
   1. Alice es la esposa del ladrón, y
   2. Alice es la esposa de Bob.
      Entonces el Inspector puede detener a Bob por robo, porque una mujer no puede ser esposa de más de un hombre.
2. Por otro lado, supongamos que el Inspector sabe:
   1. Alice es la madre del falsificador, y
   2. Alice es la madre de Charlie.
      Entonces el Inspector no sabe lo suficiente como para estar seguro de quién es el falsificador, porque podría ser algún otro hijo de Alice, en lugar de ser Charlie.

Este ejemplo ilustra una diferencia fundamental entre la\(\text{wife}\) función y la\(\text{mother}\) función: dos personas diferentes pueden tener la misma madre, pero solo una persona puede tener a una persona en particular como esposa. (Por ejemplo, si Bud y Charlie tienen la misma esposa, entonces “Bud” debe ser un apodo para Charlie). En términos matemáticos, esta importante propiedad de la función esposa se expresa diciendo que la\(\text{wife}\) función es “uno a uno”.

La noción se formaliza en la siguiente definición:

Definición\(6.4.2\).

Supongamos\(f: A \rightarrow B\). Decimos que\(f\) es uno a uno iff, para todos\(a_{1}, a_{2} \in A\), tal que\(f(a_{1}) = f(a_{2})\), tenemos\(a_{1} = a_{2}\).

Ejercicio\(6.4.3\).

Asumir\(f: A \rightarrow B\) y\(g: X \rightarrow Y\). Traducir cada aserción a la lógica de primer orden. 1) f es uno a uno. 2) g es uno a uno. 3) f no es uno a uno. 4) g no es uno a uno. (Simplifica tus respuestas en (3) y (4) para que ¬ se aplique solo a predicados.)

Obrar\(6.4.4\).

Si tiene un diagrama de flecha de una función, entonces es fácil saber si la función es o no uno a uno. Por ejemplo:

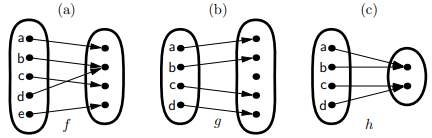
1. La función\(f\) de Figura no\(6A(a)\) es uno a uno. Esto se debe a que la flecha de\(b\) y la flecha de\(d\) van al mismo lugar, entonces\(f(b) = f(d)\). En general, si las flechas de dos elementos diferentes del dominio van al mismo elemento del rango, entonces la función no es uno a uno.
2. La función\(g\) de la Figura\(6A(b)\) es uno a uno. Esto se debe a que las flechas de dos elementos diferentes del dominio nunca van al mismo elemento del rango. En definitiva, sólo hay un elemento del dominio que va a cualquiera de los elementos del rango. (Esta es la razón de la terminología “uno a uno”. Una función es “dos a uno” si hay dos elementos del dominio mapeando a cada elemento del rango, como es cierto para la función\(h\) en la Figura\(6A(c)\), pero no necesitamos esta terminología.)
3. Advertencia. Aunque el diagrama de flechas de una función uno a uno nunca tiene más de una flecha apuntando al mismo elemento del codominio, esto no significa que cada elemento del codominio tenga exactamente una flecha dentro de él. Por ejemplo, la función\(g\) de Figura\(6A(b)\) es uno a uno (porque nunca hay más de una flecha en ningún punto), pero hay un punto en el codominio que no tiene ninguna flecha hacia él.

Figura\(6A\). Diagramas de flecha de tres funciones\(f\)\(g\),, y\(h\).

Ejemplo\(6.4.5\).

Sin dar pruebas oficiales, determinemos cuáles de las siguientes funciones son uno-a-uno.

1. \(f: \mathbb{R} \rightarrow \mathbb{R}\), definido por\(f(x) = x + 1\).
   Esto es uno a uno. Para cualquier número real\(x\) y\(y\),\(f(x) = f(y)\) significa eso\(x + 1 = y + 1\). Al restar 1 de ambos lados de la ecuación, concluimos que\(x = y\) siempre que\(f(x) = f(y)\).
2. \(g: \mathbb{R} \rightarrow \mathbb{R}\), definido por\(g(x) = |x|\). Esto no es uno a uno. Esto lo demostramos encontrando dos números reales distintos cuya imagen es la misma:\[g(1)=|1|=1=|-1|=g(-1) ,\]
   pero\(1 \neq-1\). Esto demuestra que no\(g\) es uno a uno.
3. \(f:\{1,2,3\} \rightarrow\{\mathrm{a}, \mathrm{b}, \mathrm{c}\}\)definido por\(f=\{(1, b),(2, a),(3, a)\}\).
   Esto no es uno a uno. Esto lo demostramos encontrando dos valores distintos en\(\{1,2,3\}\) cuya imagen es la misma: f (2) = a = f (3), pero 2 = 3. Esto demuestra que f no es uno a uno. 4) h: N → N, definido por h (x) = |x|. Esto es uno a uno. Como todos los números naturales son no negativos, tenemos |x| = x por cada número natural x Así que si h (x) = h (y), entonces x = |x| = h (x) = h (y) = |y| = y.

Obrar\(6.4.6\).

Estos ejemplos demuestran el patrón general de cómo probar que una función es (o no es) uno a uno:

• Para probar que una función\(f: A \rightarrow B\) es uno a uno, necesitamos demostrarlo para cada\(a_{1}, a_{2} \in A\), si\(f(a_{1}) = f(a_{2})\), entonces\(a_{1} = a_{2}\).
• Para probar que una función no\(f: A \rightarrow B\) es uno-a-uno, sólo necesitamos encontrar un solo par de valores\(a_{1}, a_{2} \in A\), para lo cual\(f(a_{1}) = f(a_{2})\), pero\(a_{1} \neq a_{2}\).

Ejercicio\(6.4.7\).

Explica por qué tus respuestas son correctas (pero no necesitas dar pruebas formales).

1. Cada fórmula define una función de\(\mathbb{R}\) a\(\mathbb{R}\). ¿Cuáles de las funciones son uno a uno?
   1. \(f(x) = 1\).
   2. \(g(x) = x\).
   3. \(h(x) = x^{2}\).
   4. \(i(x) = 3x + 2\).
   5. \(j(x) = 1/ ( |x| + 1)\).
2. Cada uno de los siguientes conjuntos de pares ordenados es una función de\(\{1,2,3,4\}\) a\(\{a, b, c, d, e\}\). ¿Cuáles son uno a uno?
   1. \(f = \{(1, a),(2, b),(3, d),(4, e)\}\)
   2. \(g = \{(1, c),(2, d),(3, d),(4, e)\}\)
   3. \(h = \{(1, e),(2, d),(3, c),(4, b)\}\)
   4. \(i = \{(1, e),(2, e),(3, e),(4, e)\}\)
   5. \(j = \{(1, a),(2, c),(3, e),(4, c)\}\)
   6. \(k = \{(1, a),(2, c),(3, e),(4, d)\}\)

Aquí hay un ejemplo de una prueba formal de que una función es uno-a-uno.

Ejemplo\(6.4.8\).

Dejar\(f: \mathbb{R} \rightarrow \mathbb{R}\) ser definido por\(f(x) = 2x + 1\). Entonces\(f\) es uno a uno.

Scratchwork. Por definición, deseamos mostrar\(\forall x_{1}, x_{2} \in \mathbb{R},\left(f\left(x_{1}\right)=f\left(x_{2}\right) \Rightarrow x_{1}=x_{2}\right)\). Así, la prueba utilizará\(\forall\) -introducción: las primeras palabras de la prueba serán “Dadas\(x_{1}, x_{2} \in \mathbb{R}\)” (u otras palabras en ese sentido). Entonces, porque deseamos mostrar\(f(x_{1}) = f(x_{2}) \Rightarrow x_{1} = x_{2}\), asumiremos\(f(x_{1}) = f(x_{2})\), y la prueba estará completa en cuanto podamos probarlo\(x_{1} = x_{2}\).

Por la definición de\(f\), el supuesto\(f(x_{1}) = f(x_{2})\) significa que\[2 x_{1}+1=2 x_{2}+1 .\]
restando 1 de ambos lados, vemos que\[2 x_{1}=2 x_{2}.\]
Dividiendo ambos lados por 2, concluimos que\(x_{1} = x_{2}\), como se desee.

Dado que se espera que los lectores de este libro de texto tengan un buen dominio de la lógica y el álgebra de secundaria, nuestra prueba oficial puede omitir los comentarios que son innecesarios para un lector tan educado. Por ejemplo, se puede esperar que el lector pueda verificar fácilmente que la ecuación se\(2x + 1 = 2x2 + 1\) puede simplificar a la ecuación\(2x_{1} = 2x_{2}\), sin que se le diga que debe restar 1 de ambos lados.

Solución

Dado\(x_{1}, x_{2} \in \mathbb{R}\), tal que\(f(x_{1}) = f(x_{2})\),\[2 x_{1}+1=2 x_{2}+1 ,\]
así\[2 x_{1}=2 x_{2} ,\]
lo tenemos\(x_{1} = x_{2}\).

Un argumento muy similar se aplica a otras funciones lineales.

Ejemplo\(6.4.9\).

Definir\(p: \mathbb{R} \rightarrow \mathbb{R}\) por\(p(z) = 6z − 100\). Demostrar que\(p\) es uno a uno.

Solución

PRUEBA.

Dado\(z_{1}, z_{2} \in \mathbb{R}\), tal que\(p(z_{1}) = p(z_{2})\),\[6 z_{1}-100=6 z_{2}-100\]
así\[6 z_{1}=6 z_{2} ,\]
lo tenemos\(z_{1} = z_{2}\).

Ejercicio\(6.4.10\).

Demostrar que cada función es uno a uno.

1. \(f: \mathbb{R} \rightarrow \mathbb{R}\)definido por\(f(x) = 3x + 5\).
2. \(f: \mathbb{R} \rightarrow \mathbb{R}\)definido por\(f(x) = 7x − 2\).
3. \(g: \mathbb{R} \rightarrow \mathbb{R}\)definido por\(g(t) = 4t + 9\).
4. \(h: \mathbb{R} \rightarrow \mathbb{R}\)definido por\(h(s) = 7 − 8s\).
5. \(i: \mathbb{R} \rightarrow \mathbb{R}\)definido por\(i(r) = (5r − 2)/7\).
6. \(j : \mathbb{Z} \rightarrow \mathbb{Z}\)definido por\(j(n) = 2n + 11\).

El hecho de que la\(\text{wife}\) función sea uno a uno puede reafirmarse como el hecho de que dos personas diferentes no pueden tener la misma esposa. En general, una función es uno a uno si dos elementos diferentes del dominio siempre se mapean a dos elementos diferentes del rango:

Una función\(f: A \rightarrow B\) es uno a uno si y solo si
\(\forall a_{1}, a_{2} \in A,\left(a_{1} \neq a_{2} \Rightarrow f\left(a_{1}\right) \neq f\left(a_{2}\right)\right).\)

(La notación “\(\forall a_{1}, a_{2} \in A\)” es la abreviatura de “\(\forall a_{1} \in A, \forall a_{2} \in A\).”)

Deberíamos justificar la aseveración en esta casilla con una prueba. La implicación\(\Rightarrow\) se demuestra en el siguiente teorema; la otra dirección es un ejercicio.

Teorema\(6.4.12\).

Si una función\(f: A \rightarrow B\) es uno a uno, entonces\[\forall a_{1}, a_{2} \in A,\left(a_{1} \neq a_{2} \Rightarrow f\left(a_{1}\right) \neq f\left(a_{2}\right)\right).\]

Prueba

\(f: A \rightarrow B\)Déjese ser uno a uno. Dado\(a_{1}, a_{2} \in A\), sabemos, por la definición de uno a uno, que\[f\left(a_{1}\right)=f\left(a_{2}\right) \Rightarrow a_{1}=a_{2} .\]

Entonces también es cierto lo contrapositivo de esta implicación. Es decir, a1 = a2 ⇒ f (a1) = f (a2).

Ejercicio\(6.4.13\).

1. Demostrar lo contrario del Teorema\(6.4.12\). Más precisamente, asumir\(f: A \rightarrow B\), y mostrar que si\[\forall a_{1}, a_{2} \in A,\left(a_{1} \neq a_{2} \Rightarrow f\left(a_{1}\right) \neq f\left(a_{2}\right)\right) ,\]
   entonces f es uno a uno.
2. Asumir:
   1. \(f: A \rightarrow B\),
   2. \(f\)es uno a uno,
   3. \(a_{1}, a_{2} \in A\),
   4. \(g: B \rightarrow C\),
   5. \(g\)es uno a uno,
   6. \(b_{1}, b_{2} \in B\),
   7. \(f(a_{1}) = b_{1}\),
   8. \(f(a_{2}) = b_{2}\), y
   9. \(g(b_{1}) = g(b_{2})\).

Espectáculo\(a_{1} = a_{2}\). [Pista: Primero usa el hecho de que\(g\) es uno a uno, luego el hecho de que\(f\) es uno a uno.]

Obrar\(6.4.14\).

(terminología alternativa). Muchos matemáticos usan la palabra “inyectable” en lugar de “uno a uno”. (Esto viene del francés.) Además, una función que es uno a uno se puede llamar inyección.