6.3: Inyecciones, Suryecciones y Biyecciones

Las funciones se utilizan frecuentemente en matemáticas para definir y describir ciertas relaciones entre conjuntos y otros objetos matemáticos. Además, las funciones se pueden utilizar para imponer ciertas estructuras matemáticas en los conjuntos. En esta sección, estudiaremos tipos especiales de funciones que se utilizan para describir estas relaciones que se llaman inyecciones y suryecciones. Antes de definir este tipo de funciones, revisaremos lo que nos dice la definición de una función y exploraremos ciertas funciones con dominios finitos.

Vista previa de la actividad\(\PageIndex{1}\): Functions with Finite Domains

Dejar\(A\) y\(B\) ser conjuntos. Dada una función\(f : A \to B\), conocemos lo siguiente:

• Para cada\(x \in A\),\(f(x) \in B\). Es decir, cada elemento de\(A\) es una entrada para la función\(f\). Esto también podría afirmarse de la siguiente manera: Para cada uno\(x \in A\), existe\(y \in B\) tal que\(y = f(x)\).
• Para un dado\(x \in A\), hay exactamente uno\(y \in B\) tal que\(y = f(x)\).

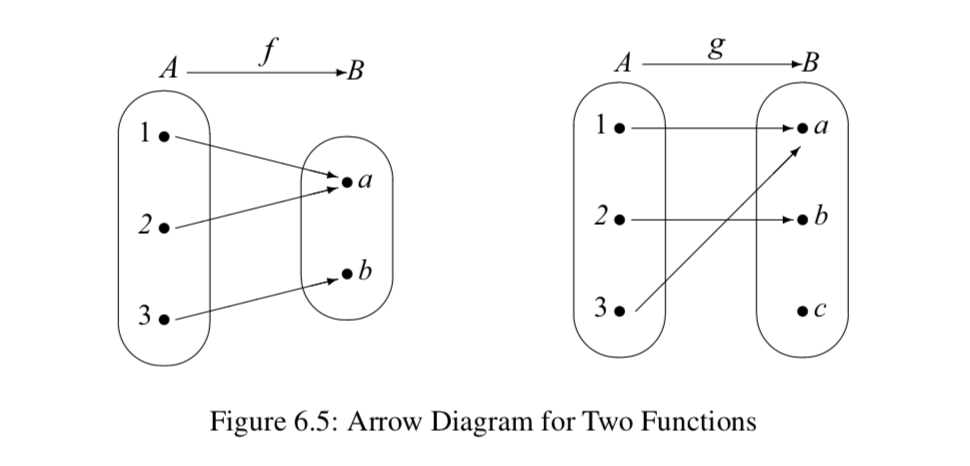
La definición de una función no requiere que diferentes entradas produzcan diferentes salidas. Es decir, es posible tener\(x_1, x_2 \in A\) con\(x1 \ne x_2\) y\(f(x_1) = f(x_2)\). El diagrama de flechas para la función\(f\) en la Figura 6.5 ilustra dicha función.

Además, la definición de una función no requiere que el rango de la función sea igual al codominio. El rango es siempre un subconjunto del codominio, pero no se requiere que estos dos conjuntos sean iguales. Es decir, si\(g: A \to B\), entonces es posible tener un\(y \in B\) tal que\(g(x) \ne y\) para todos\(x \in A\). El diagrama de flechas para la función g en la Figura 6.5 ilustra dicha función.

Ahora vamos\(A = \{1, 2, 3\}\),\(B = \{a, b, c, d\}\), y\(C = \{s, t\}\). Definir

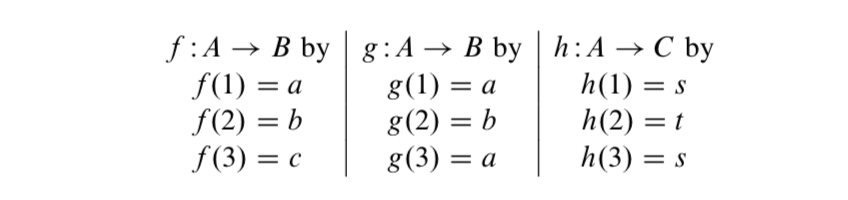
1. ¿Cuál de estas funciones satisface la siguiente propiedad para una función\(F\)?
   Para todos\(x, y \in \text{dom}(F)\), si\(x \ne y\), entonces\(F(x) \ne F(y)\).
2. ¿Cuál de estas funciones satisface la siguiente propiedad para una función\(F\)?
   Para todos\(x, y \in \text{dom}(F)\), si\(F(x) = F(y)\), entonces\(x = y\).
3. Determinar el rango de cada una de estas funciones.
4. ¿Cuáles de estas funciones tienen su rango igual a su codominio?
5. ¿Cuál de estas funciones satisface la siguiente propiedad para una función\(F\)?
   Para todos\(y\) en el codominio de\(F\), existe un\(x \in \text{dom}(F\)\) tal que\(F(x) = y\).

Vista previa de la actividad\(\PageIndex{1}\): Statements Involving Functions

Dejar\(A\) y\(B\) ser conjuntos no vacíos y dejar\(f: A \to B\). En Preview Activity\(\PageIndex{1}\), determinamos si ciertas funciones satisfacían o no algunas propiedades especificadas. Estas propiedades fueron escritas en forma de declaraciones, y ahora examinaremos estas afirmaciones con más detalle.

1. Considera la siguiente declaración:
   Para todos\(x, y \in A\), si\(x \ne y\), entonces\(f(x) \ne f(y)\).
   
   a) Escribir el contrapositivo de esta declaración condicional.
   b) Escribir la negación de esta declaración condicional.
2. Ahora consideremos la afirmación:
   Para todos\(y \in B\), existe\(x \in A\) tal que\(f(x) = y\).
   Escribe la negación de esta afirmación.
3. \(g: \mathbb{R} \to \mathbb{R}\)Déjese definir por\(g(x) = 5x + 3\), para todos\(x \in \mathbb{R}\). Complete las siguientes pruebas de las siguientes proposiciones sobre la función\(g\).
   
   Proposición 1. Para todos\(a, b \in \mathbb{R}\), si\(g(a) = g(b)\), entonces\(a = b\).
   Comprobante. Dejamos\(a, b \in \mathbb{R}\), y asumimos eso\(g(a) = g(b)\) y lo demostraremos\(a = b\). Ya que\(g(a) = g(b)\), sabemos que
   \[5a + 3 = 5b + 3.\]
   (Ahora demuestre que en esta situación,\(a = b\).)
   
   Proposición 2. Para todos\(b \in \mathbb{R}\), existe\(a \in \mathbb{R}\) tal que\(g(a) = b\).
   Comprobante. Dejamos\(b \in \mathbb{R}\). Demostraremos que existe\(a \in \mathbb{R}\) tal que\(g(a) = b\) construyendo tal\(a\) adentro\(\mathbb{R}\). Para que esto suceda, necesitamos\(g(a) = 5a + 3 = b\).
   (Ahora resolver la ecuación para\(a\) y luego mostrar que para este número real\(a\),\(g(a) = b\).)

Inyecciones

En secciones anteriores y en Preview Activity\(\PageIndex{1}\), hemos visto ejemplos de funciones para las que existen diferentes entradas que producen la misma salida. Usando notación más formal, esto significa que hay funciones\(f: A \to B\) para las que existen\(x_1, x_2 \in A\) con\(x_1 \ne x_2\) y\(f(x_1) = f(x_2)\). El trabajo en las actividades de previsualización tuvo como objetivo motivar la siguiente definición.

Definición

Dejar\(f: A \to B\) ser una función del conjunto\(A\) al conjunto\(B\). La función\(f\) se llama inyección siempre que

para todos\(x_1, x_2 \in A\), si\(x_1 \ne x_2\), entonces\(f(x_1) \ne f(x_2)\).

Cuando\(f\) es una inyección, también decimos que\(f\) es una función uno-a-uno, o que\(f\) es una función de inyección.

Observe que la condición que especifica que una función\(f\) es una inyección se da en forma de una sentencia condicional. Como veremos, en las pruebas, suele ser más fácil utilizar el contrapositivo de esta afirmación condicional. Aunque no definimos entonces el término, ya hemos escrito el contrapositivo para la declaración condicional en la definición de una inyección en la Parte (1) de Vista previa de Actividad\(\PageIndex{2}\). En esa actividad de vista previa, también escribimos la negación de la definición de una inyección. A continuación se presenta un resumen de este trabajo dando las condiciones para\(f\) ser una inyección o no ser una inyección.

Let\(f: A \to B\)

“La función\(f\) es una inyección” significa que

• para todos\(x_1, x_2 \in A\), si\(x_1 \ne x_2\), entonces\(f(x_1) \ne f(x_2)\); o
• para todos\(x_1, x_2 \in A\), si\(f(x_1) = f(x_2)\), entonces\(x_1 = x_2\).

“La función no\(f\) es una inyección” significa que

• Existen\(x_1, x_2 \in A\) tales que\(x_1 \ne x_2\) y\(f(x_1) = f(x_2)\).

Comprobación de Progreso 6.10 (Trabajando con la Definición de Inyección)

Ahora que hemos definido lo que significa para una función ser una inyección, podemos ver que en la Parte (3) de Preview Activity\(\PageIndex{2}\), probamos que la función\(g: \mathbb{R} \to \mathbb{R}\) es una inyección, donde\(g(x/) = 5x + 3\) para todos\(x \in \mathbb{R}\). Utilice la definición (o su negación) para determinar si las siguientes funciones son inyecciones o no.

1. \(k: A \to B\), dónde\(A = \{a, b, c\}\),\(B = \{1, 2, 3, 4\}\), y\(k(a) = 4, k(b) = 1\), y\(k(c) = 3\).
2. \(f: A \to C\), dónde\(A = \{a, b, c\}\),\(C = \{1, 2, 3\}\), y\(f(a) = 2, f(b) = 3\), y\(f(c) = 2\).
3. \(F: \mathbb{Z} \to \mathbb{Z}\)definido por\(F(m) = 3m + 2\) para todos\(m \in \mathbb{Z}\)
4. \(h: \mathbb{R} \to \mathbb{R}\)definido por\(h(x) = x^2 - 3x\) para todos\(x \in \mathbb{R}\)
5. \(s: \mathbb{Z}_5 \to \mathbb{Z}_5\)definido por\(sx) = x^3\) para todos\(x \in \mathbb{Z}_5\)

Contestar

Agrega textos aquí. No elimine primero este texto.

Surjecciones

En secciones anteriores y en Preview Activity\(\PageIndex{1}\), hemos visto que existen funciones\(f: A \to B\) para las que van\((f) = B\). Esto significa que cada elemento de\(B\) es una salida de la función f para alguna entrada del conjunto\(A\). Usando cuantificadores, esto significa que para cada\(y \in B\), existe\(x \in A\) tal que\(f(x) = y\). Uno de los objetivos de las actividades previas fue motivar la siguiente definición.

Definición

Dejar\(f: A \to B\) ser una función del conjunto\(A\) al conjunto\(B\). La función\(f\) se llama una sobreyección siempre que el rango de\(f\) sea igual al codominio de\(f\). Esto significa que

para cada\(y \in B\), existe\(x \in A\) tal que\(f(x) = y\).

Cuando\(f\) es una sobrejección, también decimos que\(f\) es una función onto o que se\(f\) mapea\(A\) sobre\(B\). También decimos que\(f\) es una función suryectiva.

Una de las condiciones que especifica que una función\(f\) es una sobrejección se da en forma de una declaración universalmente cuantificada, que es la declaración primaria utilizada para probar que una función es (o no es) una surjección. Aunque no definimos entonces el término, ya hemos escrito la negación para el enunciado definiendo una surjección en la Parte (2) de Vista previa de Actividad\(\PageIndex{2}\). Ahora resumimos las condiciones para\(f\) ser una sobreyección o no ser una suryección.

Let\(f: A \to B\)

“La función\(f\) es una sobrejección” significa que

• rango (\(f\)) = codom\((f) = B\); o
• Por cada\(y \in B\), existe un\(x \in A\) tal que\(f(x) = y\).

“La función no\(f\) es una sobrejección” significa que

• sonó (\(f\))\ ne codom (\(f\)); o
• Existe\(y \in B\) tal que para todos\(x \in A\),\(f(x) \ne y\).

Otro tipo importante de función es cuando una función es tanto una inyección como una sobreyección. Este tipo de función se llama biyección.

Definición

Una biyección es una función que es tanto una inyección como una sobreyección. Si la función\(f\) es una biyección, también decimos que\(f\) es uno-a-uno y onto y que\(f\) es una función biyectiva.

Comprobación de Progreso 6.11 (Trabajando con la Definición de una Sujección)

Ahora que hemos definido lo que significa para una función ser una suryección, podemos ver que en la Parte (3) de Preview Activity\(\PageIndex{2}\), probamos que la función\(g: \mathbb{R} \to \mathbb{R}\) es una surjección, donde\(g(x) = 5x + 3\) para todos\(x \in \mathbb{R}\). Determinar si las siguientes funciones son o no sobreyecciones.

1. \(k: A \to B\), dónde\(A = \{a, b, c\}\),\(B = \{1, 2, 3, 4\}\), y\(k(a) = 4, k(b) = 1\), y\(k(c) = 3\).
2. \(f: \mathbb{R} \to \mathbb{R}\)definido por\(f(x) = 3x + 2\) para todos\(x \in \mathbb{R}\).
3. \(F: \mathbb{Z} \to \mathbb{Z}\)definido por\(F(m) = 3m + 2\) para todos\(m \in \mathbb{Z}\).
4. \(s: \mathbb{Z}_5 \to \mathbb{Z}_5\)definido por\(s(x) = x^3\) para todos\(x \in \mathbb{Z}_5\).

Contestar

Agrega textos aquí. No elimine primero este texto.

La importancia del dominio y el codominio

Las funciones en los siguientes dos ejemplos ilustrarán por qué el dominio y el codominio de una función son tan importantes como la regla que define las salidas de una función cuando necesitamos determinar si la función es una suryección.

Ejemplo 6.12 (Una función que no es ni una inyección ni una sobreyección)

Dejar\(f: \mathbb{R} \to \mathbb{R}\) ser definido por\(f(x) = x^2 + 1\). Observe que

\(f(2) = 5\)y\(f(-2) = 5\).

Esto es suficiente para demostrar que la función no\(f\) es una inyección ya que esto demuestra que existen dos entradas diferentes que producen la misma salida.

Ya que\(f(x) = x^2 + 1\), eso lo sabemos\(f(x) \ge 1\) para todos\(x \in \mathbb{R}\). Esto implica que la función no\(f\) es una sobrejección. Por ejemplo, -2 está en el codominio de\(f\) y\(f(x) \ne -2\) para todos\(x\) en el dominio de\(f\).

Ejemplo 6.13 (Una función que no es una inyección sino una sobreyección)

Dejar\(T = \{y \in \mathbb{R}\ |\ y \ge 1\}\), y definir\(F: \mathbb{R} \to T\) por\(F(x) = x^2 + 1\). Al igual que en el Ejemplo 6.12, la función no\(F\) es una inyección desde entonces\(F(2) = F(-2) = 5\).

¿Es la función\(F\) una sobrejección? Es decir, ¿\(F\)\(\mathbb{R}\)mapea\(T\)? Al igual que en el Ejemplo 6.12, sí lo sabemos\(F(x) \ge 1\) para todos\(x \in \mathbb{R}\).

Para ver si se trata de una suryección, debemos determinar si es cierto que para cada\(y \in T\), existe\(x \in \mathbb{R}\) tal que\(F(x) = y\). Entonces elegimos\(y \in T\). El objetivo es determinar si existe\(x \in \mathbb{R}\) tal que

\[\begin{array} {rcl} {F(x)} &= & {y, \text { or}} \\ {x^2 + 1} &= & {y.} \end{array}\]

Una forma de proceder es trabajar hacia atrás y resolver la última ecuación (si es posible) para\(x\). Al hacerlo, obtenemos

\(x^2 = y - 1\)

\(x = \sqrt{y - 1}\)o\(x = -\sqrt{y - 1}.\)

Ahora, ya que\(y \in T\), sabemos eso\(y \ge 1\) y de ahí eso\(y - 1 \ge 0\). Esto significa que\(\sqrt{y - 1} \in \mathbb{R}\). Por lo tanto, si usamos\(x = \sqrt{y - 1}\), entonces\(x \in \mathbb{R}\), y

\[\begin{array} {rcl} {F(x)} &= & {F(\sqrt{y - 1})} \\ {} &= & {(\sqrt{y - 1})^2 + 1} \\ {} &= & {(y - 1) + 1} \\ {} &= & {y.} \end{array}\]

Esto demuestra que\(F\) es una sobrejección ya que hemos demostrado que para todos\(y \in T\), existe una

\(x \in \mathbb{R}\)tal que\(F(x) = y\). Observe que para cada uno\(y \in T\), esto fue una prueba constructiva de la existencia de\(x \in \mathbb{R}\) tal que\(F(x) = y\).

Una Lección Importante.

En los Ejemplos 6.12 y 6.13 se utilizó la misma fórmula matemática para determinar los resultados de las funciones. Sin embargo, una función no fue una sobreyección y la otra fue una sobreyección. Esto ilustra el hecho importante de que si una función es suryectiva no solo depende de la fórmula que define la salida de la función sino también del dominio y codominio de la función.

El siguiente ejemplo mostrará que si una función es o no una inyección también depende del dominio de la función.

Ejemplo 6.14 (Una función que es una inyección pero no es una sobreyección)

Vamos\(\mathbb{Z}^{\ast} = \{x \in \mathbb{Z}\ |\ x \ge 0\} = \mathbb{N} \cup \{0\}\). Definir\(g: \mathbb{Z}^{\ast} \to \mathbb{N}\) por\(g(x) = x^2 + 1\). (Observe que esta es la misma fórmula utilizada en los Ejemplos 6.12 y 6.13.) A continuación se presenta una tabla de valores para algunas entradas para la función\(g\).

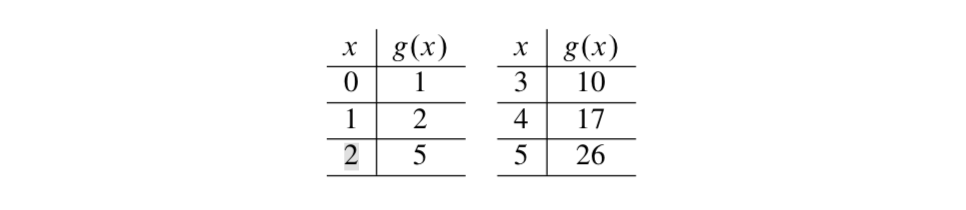
Observe que el codominio es\(\mathbb{N}\), y la tabla de valores sugiere que algunos números naturales no son salidas de esta función. Entonces parece que la función no\(g\) es una sobrejección.

Para probar que g no es una sobrejección, escoge un elemento de\(\mathbb{N}\) que no parece estar en el rango. Utilizaremos 3, y usaremos una prueba por contradicción para probar que no hay x en el dominio (\(\mathbb{Z}^{\ast}\)) tal que\(g(x) = 3\). Entonces asumimos que existe un\(x \in \mathbb{Z}^{\ast}\) con\(g(x) = 3\). Entonces

\[\begin{array} {rcl} {x^2 + 1} &= & {3} \\ {x^2} &= & {2} \\ {x} &= & {\pm \sqrt{2}.} \end{array}\]

Pero esto no es posible desde entonces\(\sqrt{2} \notin \mathbb{Z}^{\ast}\). Por lo tanto, no hay\(x \in \mathbb{Z}^{\ast}\) con\(g(x) = 3\). Esto significa que para cada\(x \in \mathbb{Z}^{\ast}\),\(g(x) \ne 3\). Por lo tanto, 3 no está en el rango de\(g\), y por lo tanto no\(g\) es una sobreyección.

La tabla de valores sugiere que diferentes entradas producen diferentes salidas, y por lo tanto eso\(g\) es una inyección. Para probar que\(g\) es una inyección, supongamos que\(s, t \in \mathbb{Z}^{\ast}\) (el dominio) con\(g(s) = g(t)\). Entonces

\[\begin{array} {rcl} {s^2 + 1} &= & {t^2 + 1} \\ {s^2} &= & {t^2.} \end{array}\]

Ya que\(s, t \in \mathbb{Z}^{\ast}\), sabemos que\(s \ge 0\) y\(t \ge 0\). Entonces la ecuación precedente implica eso\(s = t\). De ahí,\(g\) es una inyección.

Una lección importante

Todas las funciones de los tres ejemplos anteriores utilizaron la misma fórmula para determinar las salidas. Las funciones en Exam- ples 6.12 y 6.13 no son inyecciones sino que la función en el Ejemplo 6.14 es una inyección. Esto ilustra el hecho importante de que si una función es inyectiva no solo depende de la fórmula que define la salida de la función sino también del dominio de la función.

Comprobación de Progreso 6.15 (La Importancia del Dominio y Codominio)

Vamos\(R^{+} = \{y \in \mathbb{R}\ |\ y > 0\}\). Definir

\ [\ begin {array} {rcl} {f} &: & {\ mathbb {R}\ a\ mathbb {R}\ text {by} f (x) = e^ {-x},\ text {para cada} x\ in\ mathbb {R},\ texto {y}}\\ {g} &: & {\ mathbb {R}\ a\ mathbb {R}\ a\ mathbb {R} ^ {+}\ texto {por} g (x) = e^ {-x},\ texto {para cada} x\ in\ mathbb {R}.}

Determinar si cada una de estas funciones es una inyección o una sobreyección. Justifica tus conclusiones. Nota: Antes de escribir pruebas, podría ser útil dibujar la gráfica de\(y = e^{-x}\). Se puede obtener una gráfica razonable usando\(-3 \le x \le 3\) y\(-2 \le y \le 10\). Por favor, ten en cuenta que la gráfica es no prueba tus conclusiones, pero puede ayudarte a llegar a las conclusiones correctas, que aún necesitarán pruebas.

Contestar

Agrega textos aquí. No borre primero este texto.

Trabajar con una función de dos variables

Se necesita tiempo y práctica para llegar a ser eficiente en el trabajo con las definiciones formales de inyección y suryección. Como hemos visto, todas las partes de una función son importantes (el dominio, el codominio y la regla para determinar los resultados). Esto es especialmente cierto para funciones de dos variables.

Por ejemplo, definimos\(f: \mathbb{R} \times \mathbb{R} \to \mathbb{R} \times \mathbb{R}\) por

\(f(a, b) = (2a + b, a - b)\)para todos\((a, b) \in \mathbb{R} \times \mathbb{R}\).

Observe que tanto el dominio como el codominio de esta función es el conjunto\(\mathbb{R} \times \mathbb{R}\). Así, las entradas y las salidas de esta función son pares ordenados de números reales. Por ejemplo,

\(f(1, 1) = (3, 0)\)y\(f(-1, 2) = (0, -3)\).

Para explorar cuál\(f\) es o no una inyección, asumimos que\((a, b) \in \mathbb{R} \times \mathbb{R}\),\((c, d) \in \mathbb{R} \times \mathbb{R}\), y\(f(a,b) = f(c,d)\). Esto significa que

\((2a + b, a - b) = (2c + d, c - d)\).

Como esta ecuación es una igualdad de pares ordenados, vemos que

\[\begin{array} {rcl} {2a + b} &= & {2c + d, \text{ and }} \\ {a - b} &= & {c - d.} \end{array}\]

Al sumar los lados correspondientes de las dos ecuaciones en este sistema, obtenemos\(3a = 3c\) y por lo tanto,\(a = c\). Sustituir\(a = c\) en cualquiera de las dos ecuaciones en el sistema nos da\(b = d\). Desde\(a = c\) y\(b = d\), concluimos que

\((a, b) = (c, d)\).

De ahí que hayamos demostrado que si\(f(a, b) = f(c, d)\), entonces\((a, b) = (c, d)\). Por lo tanto,\(f\) es una inyección.

Ahora, para determinar si\(f\) es una suryección, dejamos\((r, s) \in \mathbb{R} \times \mathbb{R}\), donde\((r, s)\) se considera que es un elemento arbitrario del codominio de la función f. ¿Podemos encontrar un par ordenado\((a, b) \in \mathbb{R} \times \mathbb{R}\) tal que\(f(a, b) = (r, s)\)? Trabajando hacia atrás, vemos que para hacer esto, necesitamos

\((2a + b, a - b) = (r, s).\)

Es decir, necesitamos

\(2a + b = r\)y\(a - b = s\).

Resolver este sistema para\(a\) y\(b\) rendimientos

\(a = \dfrac{r + s}{3}\)y\(b = \dfrac{r - 2s}{3}\).

Ya que\(r, s \in \mathbb{R}\), podemos concluir eso\(a \in \mathbb{R}\)\(b \in \mathbb{R}\) y por lo tanto eso\((a, b) \in \mathbb{R} \times \mathbb{R}\).

Ahora necesitamos verificar eso para. estos valores de\(a\) y\(b\), obtenemos\(f(a, b) = (r, s)\). Entonces

\[\begin{array} {rcl} {f(a, b)} &= & {f(\dfrac{r + s}{3}, \dfrac{r - 2s}{3})} \\ {} &= & {(2(\dfrac{r + s}{3}) + \dfrac{r - 2s}{3}, \dfrac{r + s}{3} - \dfrac{r - 2s}{3})} \\ {} &= & {(\dfrac{2r + 2s + r - 2s}{3}, \dfrac{r + s - r + 2s}{3})} \\ {} &= & {(r, s).} \end{array}\]

Esto prueba que para todos\((r, s) \in \mathbb{R} \times \mathbb{R}\), existe\((a, b) \in \mathbb{R} \times \mathbb{R}\) tal que\(f(a, b) = (r, s)\). De ahí que la función\(f\) sea una sobreyección. Ya que\(f\) es tanto una inyección como una sobreyección, es una biyección.

Comprobación de progreso 6.16 (Una función de dos variables)

\(g: \mathbb{R} \times \mathbb{R} \to \mathbb{R}\)Déjese definir por\(g(x, y) = 2x + y\), para todos\((x, y) \in \mathbb{R} \times \mathbb{R}\).

Nota: ¡Ten cuidado! Una diferencia importante entre esta función y el ejemplo anterior es que para la función\(g\), el codominio es\(\mathbb{R}\), no\(\mathbb{R} \times \mathbb{R}\). Es una buena idea comenzar por computar varias salidas para varias entradas (y recordar que las entradas son pares ordenados).

1. Observe que el par ordenado\((1, 0) \in \mathbb{R} \times \mathbb{R}\). Es decir (1, 0) está en el dominio de\(g\). También fíjese en eso\(g(1, 0) = 2\). ¿Es posible encontrar otro par ordenado\((a, b) \in \mathbb{R} \times \mathbb{R}\) tal que\(g(a, b) = 2\)?
2. Vamos\(z \in \mathbb{R}\). Entonces\((0, z) \in \mathbb{R} \times \mathbb{R}\) y así\((0, z) \in \text{dom}(g)\). Ahora determinar\(g(0, z)\)?
3. ¿La función es\(g\) una inyección? ¿Es la función\(g\) una sobrejección? Justifica tus conclusiones.

Contestar

Agrega textos aquí. No borre primero este texto.

Ejercicio 6.3

1. (a) Dibuja un diagrama de flechas que represente una función que es una inyección pero no es una suryección.
   (b) Dibujar un diagrama de flechas que represente una función que es una inyección y es una suryección.
   (c) Dibujar un diagrama de flechas que represente una función que no es una inyección y no es una sobreyección.
   (d) Dibujar un diagrama de flechas que represente una función que no es una inyección sino una sobreyección.
   (e) Dibujar un diagrama de flechas que represente una función que no sea una biyección.
2. Dejar\(\mathbb{Z}_5 = \{0, 1, 2, 3, 4\}\) y dejar\(\mathbb{Z}_6 = \{0, 1, 2, 3, 4, 5\}\). Para cada una de las siguientes funciones, determine si la función es una inyección y determine si la función es una sobreyección. Justificar todas las conclusiones
   
   (a)\(f: \mathbb{Z}_5 \to \mathbb{Z}_5\) por\(f(x) = x^2 + 4\) (mod 5), para todos\(x \in \mathbb{Z}_5\)
   (b)\(g: \mathbb{Z}_6 \to \mathbb{Z}_6\) por\(g(x) = x^2 + 4\) (mod 6), para todos\(x \in \mathbb{Z}_6\)
   (c)\(F: \mathbb{Z}_5 \to \mathbb{Z}_5\) por\(F(x) = x^3 + 4\) (mod 5), para todos\(x \in \mathbb{Z}_5\)
3. Para cada una de las siguientes funciones, determine si la función es una inyección y determine si la función es una sobreyección. Justificar todas las conclusiones
   
   (a)\(f: \mathbb{Z} \to \mathbb{Z}\) definido por\(f(x) = 3x + 1\), para todos\(x \in \mathbb{Z}\).
   (b)\(F: \mathbb{Q} \to \mathbb{Q}\) definido por\(F(x) = 3x + 1\), para todos\(x \in \mathbb{Q}\).
   (c)\(g: \mathbb{R} \to \mathbb{R}\) definido por\(g(x) = x^3\), para todos\(x \in \mathbb{R}\).
   (d)\(G: \mathbb{Q} \to \mathbb{Q}\) definido por\(G(x) = x^3\), para todos\(x \in \mathbb{Q}\).
   (e)\(k: \mathbb{R} \to \mathbb{R}\) definido por\(k(x) = e^{-x^2}\), para todos\(x \in \mathbb{R}\).
   f)\(K: \mathbb{R}^{\ast} \to \mathbb{R}\) definido por\(K(x) = e^{-x^2}\), para todos\(x \in \mathbb{R}^{\ast}\).
   Nota:\(\mathbb{R}^{\ast} = \{x \in \mathbb{R}\ |\ x \ge 0\}.\)
   (g)\(K_1: \mathbb{R}^{\ast} \to T\) definido por\(K_1(x) = e^{-x^2}\), para todos\(x \in \mathbb{R}^{\ast}\), donde\(T = \{y \in \mathbb{R}\ |\ 0 < y \le 1\}\).
   (h)\(h: \mathbb{R} \to \mathbb{R}\) definido por\(h(x) = \dfrac{2x}{x^2 + 4}\), para todos\(x \in \mathbb{R}\).
   (i)\(H: \{x \in \mathbb{R}\ |\ x \ge 0\} \to \{y \in \mathbb{R}\ |\ 0 \le y \le \dfrac{1}{2}\}\) definido por\(H(x) = \dfrac{2x}{x^2 + 4}\), para todos\(x \in \{x \in \mathbb{R}\ |\ x \ge 0\}\).
4. Para cada una de las siguientes funciones, determine si la función es una biyección. Justificar todas las conclusiones
   
   (a)\(F: \mathbb{R} \to \mathbb{R}\) definido por\(F(x) = 5x + 3\), para todos\(x \in \mathbb{R}\).
   (b)\(G: \mathbb{Z} \to \mathbb{Z}\) definido por\(G(x) = 5x + 3\), para todos\(x \in \mathbb{Z}\).
   (c)\(f: (\mathbb{R} - \{4\}) \to \mathbb{R}\) definido por\(f(x) = \dfrac{3x}{x - 4}\), para todos\(x \in (\mathbb{R} - \{4\})\).
   (d)\(g: (\mathbb{R} - \{4\}) \to (\mathbb{R} - \{3\})\) definido por\(g(x) = \dfrac{3x}{x - 4}\), para todos\(x \in (\mathbb{R} - \{4\})\).
5. Let\(s: \mathbb{N} \to \mathbb{N}\), donde para cada uno\(n \in \mathbb{N}\),\(s(n)\) es la suma de los distintos divisores numéricos naturales de\(n\). Esta es la suma de la función de divisores que se introdujo en la Vista previa\(\PageIndex{2}\) de la Actividad de la Sección 6.1. ¿Es\(s\) una inyección? ¿Es\(s\) una sobrejección? Justifica tus conclusiones.
6. Let\(d: \mathbb{N} \to \mathbb{N}\), donde\(d(n)\) esta el numero de divisores numeros naturales de\(n\). Esta es la función de número de divisores introducida en el Ejercicio (6) de la Sección 6.1. ¿La función es\(d\) una inyección? ¿Es la función\(d\) una sobrejección? Justifica tus conclusiones.
7. En Vista previa\(\PageIndex{2}\) de la Actividad de la Sección 6.1, presentamos la función de cumpleaños. ¿La función de cumpleaños es una inyección? ¿Es una sobrejección? Justifica tus conclusiones.
8. (a) Que\(f: \mathbb{Z} \times \mathbb{Z} \to \mathbb{Z}\) se defina por\(f(m,n) = 2m + n\). ¿La función es\(f\) una inyección? ¿Es la función\(f\) una sobrejección? Justifica tus conclusiones.
   (b) Que\(g: \mathbb{Z} \times \mathbb{Z} \to \mathbb{Z}\) se defina por\(g(m,n) = 6m + 3n\). ¿La función es\(g\) una inyección? ¿Es la función\(g\) una sobrejección? Justifica tus conclusiones.
9. (a) Que\(f: \mathbb{R} \times \mathbb{R} \to \mathbb{R} \times \mathbb{R}\) se defina por\(f(x,y) = (2x, x + y)\). ¿La función es\(f\) una inyección? ¿Es la función\(f\) una sobrejección? Justifica tus conclusiones.
   (b) Que\(g: \mathbb{Z} \times \mathbb{Z} \to \mathbb{Z} \times \mathbb{Z}\) se defina por\(g(x,y) = (2x, x + y)\). ¿La función es\(g\) una inyección? ¿Es la función\(g\) una sobrejección? Justifica tus conclusiones.
10. Dejar\(f: \mathbb{R} \times \mathbb{R} \to \mathbb{R}\) ser la función definida por\(f(x, y) = -x^2y + 3y\), para todos\((x, y) \in \mathbb{R} \times \mathbb{R}\). ¿Es la función\(f\) y la inyección? ¿Es la función\(f\) una sobrejección? Justifica tus conclusiones.
11. Dejar\(g: \mathbb{R} \times \mathbb{R} \to \mathbb{R}\) ser la función definida por\(g(x, y) = (x^3 + 2)sin y\), para todos\((x, y) \in \mathbb{R} \times \mathbb{R}\). ¿Es la función\(g\) y la inyección? ¿Es la función\(g\) una sobrejección? Justifica tus conclusiones.
12. Dejar\(A\) ser un conjunto no vacío. La función de identidad en el conjunto\(A\), denotada por\(I_A\), es la función\(I_A: A \to A\) definida por\(I_A (x) = x\) para cada\(x\) entrada\(A\). ¿Es\(I_A\) una inyección? ¿Es\(I_A\) una sobrejección? Justifica tus conclusiones.
13. Dejar\(A\) y\(B\) ser dos conjuntos no vacíos. Definir
    \[p_1: A \times B \to A \text{ by } p_1(a, b) = a\]
    para cada\((a, b) \in A \times B\). Esa es la primera función de proyección introducida en el Ejercicio (5) en la Sección 6.2.
    a) ¿Es la función\(p_1\) una sobrejección? Justifica tu conclusión.
    b) Si\(B = \{b\}\), ¿la función es\(p_1\) una inyección? Justifica tu conclusión.
    c) ¿Bajo qué condición (s)\(p_1\) no es la función una inyección? Haz una conjetura y demuéstrala.
14. Definir\(f: \mathbb{N} \to \mathbb{Z}\) se definirá de la siguiente manera: Para cada uno\(n \in \mathbb{N}\),
    \[f(n) = \dfrac{1 + (-1)^n (2n - 1)}{4}.\]
    ¿La función es\(f\) una inyección? ¿Es la función\(f\) una sobrejección? Justifica tus conclusiones.
    
    Sugerencias. Comience calculando varias salidas para la función antes de intentar escribir una prueba. Al explorar si la función es o no una inyección, podría ser una buena idea usar casos basados en si las entradas son pares o impares. Al explorar si f es una sobreyección, considere usar casos basados en si la salida es positiva o menor o igual a cero.
15. Dejar\(C\) ser el conjunto de todas las funciones reales que son continuas en el intervalo cerrado [0, 1]. Defina la función de la\(A: C \to \mathbb{R}\) siguiente manera: Para cada uno\(f \in C\).
    \[A(f) = \int_0^1 f(x)dx.\]
    ¿La función es\(A\) una inyección? ¿Es una sobrejección? Justifica tus conclusiones.
16. Vamos\(A = \{(m, n)\ |\ m \in \mathbb{Z}, n \in \mathbb{Z}, \text{ and } n \ne 0\}\). Definir de la\(f: A \to \mathbb{Q}\) siguiente manera:
    Para cada uno\((m, n) \in A\),\(f(m, n) = \dfrac{m + n}{n}\).
    a) ¿La función f es una inyección? Justifica tu conclusión.
    b) ¿La función f es una sobrejección? Justifica tu conclusión.
17. Evaluación de pruebas
    Consulte las instrucciones para Ejercicio (19) en la página 100 de la Sección 3.1.
    

    (a)

    Proposición. La función\(f: \mathbb{R} \times \mathbb{R} \to \mathbb{R} \times \mathbb{R}\) definida por\(f(x, y) = (2x + y, x - y)\) es una inyección.

    Prueba

    Para cada uno\((a, b)\) y\((c, d)\) en\(\mathbb{R} \times \mathbb{R}\), si\(f(a, b) = f(c, d)\), entonces

    \((2a + b, a - b) = (2c + d, c - d).\)

    Usaremos sistemas de ecuaciones para demostrarlo\(a = c\) y\(b = d\).

    \[\begin{array} {rcl} {2a + b} &= & {2c + d} \\ {a - b} &= & {c - d} \\ {3a} &= & {3c} \\ {a} &= & {c} \end{array}\]

    Ya que\(a = c\), vemos que

    \((2c + b, c - b) = (2c + d, c - d).\)

    Entonces\(b = d\). Por lo tanto, hemos demostrado que la función\(f\) es una inyección.

    b)

    Proposición. La función\(f: \mathbb{R} \times \mathbb{R} \to \mathbb{R} \times \mathbb{R}\) definida por\(f(x, y) = (2x + y, x - y)\) es una sobreyección.

    Prueba

    Necesitamos encontrar un par ordenado tal que\(f(x, y) = (a, b)\) para cada uno\((a, b)\) en\(\mathbb{R} \times \mathbb{R}\). Es decir, necesitamos\((2x + y, x - y) = (a, b)\), o

    \(2x + y = a\)y\(x - y = b\).

    Tratando estas dos ecuaciones como un sistema de ecuaciones y resolviendo para\(x\) y\(y\), encontramos que

    \(x = \dfrac{a + b}{3}\)y\(y = \dfrac{a - 2b}{3}\).

    Por lo tanto,\(x\) y\(y\) son números reales,\((x, y) \in \mathbb{R} \times \mathbb{R}\), y

    \[\begin{array} {rcl} {f(x, y)} &= & {f(\dfrac{a + b}{3}, \dfrac{a - 2b}{3})} \\ {} &= & {(2(\dfrac{a + b}{3}) + \dfrac{a - 2b}{3}, \dfrac{a + b}{3} - \dfrac{a - 2b}{3})} \\ {} &= & {(\dfrac{2a + 2b + a - 2b}{3}, \dfrac{a + b - a + 2b}{3})} \\ {} &= & {(\dfrac{3a}{3}, \dfrac{3b}{3})} \\ {} &= & {(a, b).} \end{array}\]

    Por lo tanto, nosotros. hemos demostrado que para cada\((a, b) \in \mathbb{R} \times \mathbb{R}\), existe\((x, y) \in \mathbb{R} \times \mathbb{R}\) tal que\(f(x, y) = (a, b)\). Esto demuestra que la función\(f\) es una sobreyección.

    Exploraciones y actividades

18. Funciones definidas por partes. A menudo decimos que una función es una función definida por partes si tiene reglas diferentes para determinar la salida para diferentes partes de su dominio. Por ejemplo, podemos definir una función\(f: \mathbb{R} \to \mathbb{R}\) dando una regla para calcular\(f(x)\) cuándo\(x \ge 0\) y dando una regla para calcular\(f(x)\) cuándo x < 0 de la siguiente manera:
    \[f(x) = \begin{cases} x^2 + 1, & \text{ if \(x\) \(\ge\) 0;} \\ x - 1 & \text{ if \(x\) < 0.} \end{cases}\]
    (a) Esbozar una gráfica de la función\(f\). ¿Es la función\(f\) y la inyección? ¿Es la función\(f\) una sobrejección? Justifica tus conclusiones.
    
    Para cada una de las siguientes funciones, determine si la función es una inyección y determine si la función es una sobreyección. Justificar todas las conclusiones
    
    b)\(g: [0, 1] \to (0, 1)\) por
    \[g(x) = \begin{cases} 0.8, & \text{ if \(x = 0\);} \\ 0.5x & \text{ if \(0 < x < 1\);} \\ 0.6 & \text{ if \(x = 1\).} \end{cases}\]
    c)\(h: \mathbb{Z} \to \{0, 1\}\) por
    \[h(x) = \begin{cases} 0, & \text{ if \(x\) is even;} \\ 1, & \text{ if \(x\) is odd.} \end{cases}\]
19. Funciones Cuyo Dominio es\(\mathcal{M}_2(\mathbb{R})\). \(\mathcal{M}_2(\mathbb{R})\)Let. representar el conjunto de todas 2 por 2 matrices sobre\(\mathbb{R}\).
    
    (a) Defien det:\(\mathcal{M}_2(\mathbb{R}) \to \mathbb{R}\) por
    \ [det
    \ left [{\ begin {array} {cc}
    a & b\\
    c & d\\
    \ end {array}}\ right]
    = ad - bc.\]
    Esta es la función determinante introducida en el Ejercicio (9) de la Sección 6.2. ¿La función determinante es una inyección? ¿La función determinante es una sobreyección? Justifica tus conclusiones.
    
    (b) Definir tran:\(\mathcal{M}_2(\mathbb{R}) \to \mathcal{M}_2(\mathbb{R})\) por
    \ [tran
    \ left [{\ begin {array} {cc}
    a & b\\
    c & d\\
    \ end {array}}\ right]
    = A^T =
    \ left [{\ begin {array} {cc}
    a & c\\
    b & d\\
    \ end {array}}\ right].\]
    Esta es la función de transposición introducida en el Ejercicio (10) de la Sección 6.2. ¿La función transpuesta es una inyección? ¿La función transpuesta es una sobreyección? Justifica tus conclusiones.
    
    (c) Definir\(F: \mathcal{M}_2(\mathbb{R}) \to \mathbb{R}\) por
    \ [F
    \ left [{\ begin {array} {cc}
    a & b\\
    c & d\
    \ end {array}}\ right]
    = a^2 + d^2 - b^2 - c^2.\]
    Es la función\(F\) una inyección? ¿Es la función\(F\) una sobrejección? Justifica tus conclusiones.

Contestar

Agrega textos aquí. No borre primero este texto.